 |
Методика эксперимента и описание установки
|
|
|
|
Выражения (4), (5) и (6), полученные с использованием статистики Ферми-Дирака, могут быть проверены экспериментально. На рис.1 схематично изображена экспериментальная установка.
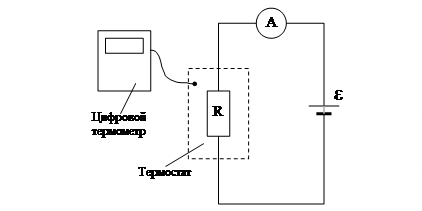
Рис. 1. Блок-схема экспериментальной установки.
Полупроводниковый образец сопротивлением R подключают к источнику напряжения e и помещают в термостат. В установке предусмотрена возможность плавного изменения температуры термостата и ее измерения цифровым термометром. Поскольку ток в цепи пропорционален проводимости полупроводника, то выражение (4) можно записать в виде[3]:
I = I 0 exp (− E g / 2 kT), (7)
где I 0 – коэффициент слабо зависящий от температуры.
Из (7) получаем:
ln (I) = − (E g / 2 k) T −1 + ln (I 0), (8)
Изменяя температуру термостата и измеряя ее цифровым термометром, снимают величину тока в цепи полупроводникового сопротивления с собственной проводимостью при постоянном напряжении e. По результатам измерений строится график зависимости ln (I)от Т −1 (рис.2). Тангенс угла наклона этой прямой определяется величиной ширины запрещенной зоны, что позволяет вычислить значение E g.

Рис.2 Зависимость логарифма тока от величины обратной температуре
для полупроводников с собственной проводимостью.
Линейная зависимость (8) во всем диапазоне температур свидетельствует о сохранении собственной проводимости полупроводника. Если исследуется полупроводник с примесной проводимостью, то
σ = σ 0 + σ прим, (9)
где σ прим примесная проводимость. С увеличением температуры образца возможно изменение типа проводимости, как указывалось выше. Тогда график зависимости ln (I) = f (T −1) может иметь излом (рис.3.), который свидетельствует об изменении типа проводимости. Измеряя тангенсы наклона линейных участков графика, оказывается возможным определить не только энергию запрещенной зоны, но и энергию положения примесного уровня Е прим= Е а (или Е d). На рис.3. участок АВ соответствует примесной проводимости, ВС – „истощению” примесей и СD- собственной проводимости полупроводника. Поведение графика на участке ВС может быть сложнее нежели изображено на рис.3., что связано с фазовыми переходами при нагреве образца.
|
|
|

Рис. 3. Зависимость логарифма тока от величины обратной температуре
для полупроводников с примесной проводимостью.
Термосопротивления на основе полупроводников находят широкое применение в термометрах, измеряющих температуру в диапазоне от -1000С до +3000С. Принципиальная схема такого термометра ничем не отличается от изображенной на рис. 1, а амперметр проградуирован в градусах. Полупроводниковые термосопротивления также используется для регистрации слабых тепловых сигналов. Высокая чувствительность подобных приборов позволяет конструировать на их основе приемники теплового излучения, реагирующие на тепловые потоки мощностью до 10−10 Вт.
Конструкция установки
Экспериментальная установка выполнена в виде отдельного функционального модуля, заключенного в металлический кожух, на лицевой панели которого расположены:
- мультиметр для измерения тока и напряжения при снятии вольт-амперных характеристик;
- тумблер «I-U» - для переключения мультиметра из режима измерения тока в режим измерения напряжения;
- цифровой индикатор термометра;
- тумблер включения термометра – «термометр»;
- ручка регулировки напряжения на полупроводниковом сопротивлении – «U»;
- тумблер включения печи нагревателя – «нагреватель»;
- ручка регулировки нагрева печи термостата – «нагрев» (позиция против часовой стрелки до упора – печь выключена);
|
|
|
- переключатель «R1-R2» полупроводниковых сопротивлений (R2 – с собственной проводимостью, R1- с примесной проводимостью);
- тумблер включения установки – «сеть».
Величина силы тока протекающего через сопротивления определяется по напряжению на резисторе в 1 Ом, который подключен последовательно с полупроводниками. При этом тумблер « I-U » переводится в положение « I », а величина тока определяется по шкале « 200 mV » мультиметра.
|
|
|


