 |
Порядок выполнения работы и обработка результатов
|
|
|
|
1.Перед началом работы проверьте, что ручка «выход» генератора находится в крайнем левом положении, а в стеклянной трубке отсутствуют капли воды. При необходимости перед началом эксперимента трубку следует насухо протереть.
2.Залить исследуемую жидкость в ячейку между двумя рисками.
3.Включить установку тумблером «сеть», и источник излучения тумблером «лампа».
4.Не включая УЗГ измерить интенсивность прошедшего излучения 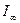 в верхней части трубки.
в верхней части трубки.
5.Включить генератор тумблером «сеть», расположенным на самом генераторе. Постепенно увеличивая поток частиц жидкости ручкой генератора «выход», установить такое их распределение по высоте столба, при котором столб частиц будет занимать всю высоту трубки при минимальной концентрации в верхней ее части.
6.Перемещая вдоль трубки оптико-измерительную систему, по показаниям вольтметра измерить интенсивности излучения 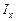 на различных высотах
на различных высотах  . Полученные данные записать в таблицу 1.
. Полученные данные записать в таблицу 1.
Таблица 1.
Высота столба
 , см , см
|
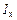 , мВ , мВ
| 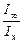
| 
|
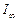 =
=
7.Исходя из результатов измерений рассчитать по формуле (9) логарифм отношения концентраций. Данные занести в таблицу 1.
8.Построить график зависимости  от
от  и в линейной области графика вычислить коэффициент γ по формуле (11).
и в линейной области графика вычислить коэффициент γ по формуле (11).
9.Рассчитать эффективную температуру частиц воды в столбе по формуле (12), считая что средний диаметр частиц составляет d ≈0,05 мкм. Сравнить полученную температуру с температурой жидкости в ячейке и температурой стенок стеклянной трубки.
Контрольные вопросы
1. Запишите аналитическое выражения распределения Больцмана. Поясните физический смысл величин, входящих в это выражение.
|
|
|
2. Равновесием каких потоков частиц устанавливается их распределение в настоящей работе?
3. Применив распределение Больцмана к атмосферному воздуху над поверхностью Земли, получите барометрическую формулу, устанавливающую распределение давления воздуха над поверхностью Земли.
4. В чем состоит закон Бугера-Ламберта?
ЛИТЕРАТУРА
1. Детлаф А.А., Яворский Б.М. Курс физики. М., Высшая школа, 1989.
2. Перник А.Д. Проблемы кавитации. Л., 1966.
3. Кнэпп Р., Дейли Дж., Хэммит Ф. Кавитация. М., Наука,1974.
4. Сивухин Д.В. Общий курс физики. М., Наука, 1983.
5. Савельев И.А. Курс общей физики. М., Астрель, АСТ, 2002.
Л А Б О Р А Т О Р Н А Я Р А Б О Т А № 71е
Термо-ЭДС при контакте металлов
Целью работы является изучении статистики Ферми-Дирака применительно к описанию электронов в металлах.
Введение
Электроны, как частицы с полуцелым спином, подчиняются статистике Ферми-Дирака, в которой функция распределения имеет вид [1]:
f (Е) = { exp [(E – m) /kT ] + 1} – 1, (1)
где Е – энергия электрона, а m -химический потенциал. Исследовать применение статистики Ферми-Дирака к описанию электронов в металлах можно на примере эффекта Зеебека [1], то есть изучая термоэлектрические явления, возникающие при контакте металлов. Величина контактной разности потенциалов зависит от многих факторов, но прежде всего от природы граничащих веществ. Контактные явления широко используются в технике, например, для измерения температур.
Если создать замкнутую цепь из двух проводников и поддерживать их контакты при разных температурах Т 1 и Т 2, то в цепи возникает термо-ЭДС e T. Открывший это явление в 1921 г. Зеебек, получил на опыте линейную зависимость e T от разности температур:
e T = a D Т. (2)
Параметр a называется удельной термо-ЭДС данной пары металлов или полупроводников. В дальнейшем выяснилось, что для разных материалов a зависит от Т довольно сложным образом, вплоть до того, что может менять знак.
|
|
|
Одной из причин возникновения термо-ЭДС в цепи (см. рис.1) является наличие внутренней контактной разности потенциалов U на границе раздела металлов М1 и М2 с разными уровнями Ферми, которые являются функцией температуры [1]:
U = [ E F1(T) – E F2(T)]/ е. (3)
Здесь E F1(T) и E F2(T) – энергия Ферми первого и второго металла, е – заряд электрона. При Т 1= Т 2, U в верхнем и нижнем контакте равны по величине и имеют противоположные знаки, поэтому тока в такой цепи не будет. Если Т 1 ≠ Т 2, то скачок потенциала при переходе из одного металла в другой для спаев, находящихся при разных температурах неодинаков, и сумма скачков потенциалов отлична от нуля. Учитывая, что суммарная разность потенциалов при обходе по замкнутому контуру равна нулю, для направления обхода, показанного на рис.1 стрелкой, получаем [1]:
e T= U 12(T 1) + U 21(T 2) = e –1{[ E F1(T 1) – E F2(T 1)] + [ E F2(T 2) – E F1(T 2)]} =
= e –1[ E F2(T 2) – E F2(T 1)] – [ E F1(T 2) – E F1(T 1)]}
Каждое из слагаемых в квадратных скобках можно представить как результат интегрирования:
e T  (4)
(4)
Учитывая, что зависимость энергии Ферми от температуры определяется выражением [2]:
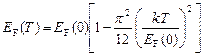 , (5)
, (5)

Рис.1 Контакт двух металлов
интегралы (4) легко вычисляются. Здесь E F(0) – энергия Ферми при Т =0К. Проведя необходимые выкладки, получаем:
e T  (6)
(6)
Таким образом, e T зависит от разности квадратов температур. Однако, если Т 2 и Т 1 отличаются друг от друга незначительно, то
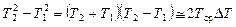 ,
,
где Т ср – средняя температура контактов, а Δ Т – разность температур контактов. Тогда (6) можно представить в виде:
e T 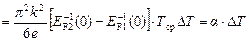 , (7)
, (7)
где a несильно зависит от температуры.
Кроме рассмотренной выше причины возникновения термо-ЭДС, есть и другие процессы, влияющие на появление стороннего поля в проводниках, связанные с градиентом температуры вдоль проводников: диффузия электронов (или дырок) и увлечение электронов фононами. Оба процесса, приводящие к образованию избытка электронов вблизи холодного конца проводника и недостатка их вблизи горячего конца, подробно рассмотрены в [1], однако их вклад в термо-ЭДС в настоящей работе незначителен [3].
|
|
|
Термопарой или термоэлементом называется цепь из двух разнородных проводников, концы которых электрически соединены, например сваркой. Термопара может быть использована для измерения температуры после предварительной градуировки, т.е. экспериментального определения зависимости e T = f (T) при разных температурах Т рабочего конца и постоянной определенной температуре Т 0 свободного конца. Плавная, приближающаяся к линейной, зависимости термо-ЭДС обеспечивает большое удобство градуировки термопары. C помощью термопар можно измерять с точностью до сотых долей кельвина как низкие так и высокие температуры.
|
|
|


