 |
Числовые характеристики случайных величин.
|
|
|
|
(А.Н.Ремизов, 1987, стр.34-37, А.Н.Ремизов, 1999, стр.27-30, Н.Л.Лобоцкая,1978, стр. 353).
Во многих случаях наряду с распределение случайной величины или вместо него информацию об этих величинах могут дать числовые параметры, получившие название числовых характеристик случайной величины. Наиболее употребительные из них:
1. Математическое ожидание - (среднее значение) случайной величины есть сумма произведений всех возможных ее значений на вероятности этих значений:
М(Х) = x1 ´ р1 + x2 ´ р2 + x3 ´ р3 + ¼ + xn ´ рn = å xi ´ рi
2. Дисперсия случайной величины:
D(X)= å(M(X) - xi)2 ´ рi
3. Среднее квадратическое отклонение:
 s = Ö D(X)
s = Ö D(X)
Правило “ТРЕХ СИГМ ” - если случайная величина распределена по нормальному закону, то отклонение этой величины от среднего значения по абсолютной величине не превосходит утроенного среднего квадратического отклонения M(X)±3s
НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ
(А.Н.Ремизов, 1987,стр.37-40, Н.Л.Лобоцкая,1978, стр. 348).
Наиболее часто встречаются величины, распределенные по нормальному закону (закон Гаусса). Г л а в н а я о с о б е н н о с т ь - он является предельным законом, к которому приближаются другие законы распределения.
Случайная величина распределена по нормальному закону, если плотность вероятности ее имеет вид:
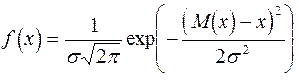
где
M(X) - математическое ожидание случайной величины;
s - среднее квадратическое отклонение.
 |
| График плотности вероятности нормально распределённой величины |
Плотность вероятности (функция распределения) показывает, как меняется вероятность, отнесенная к интервалу dx случайной величины, в зависимости от значения самой величины: 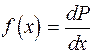
ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
|
|
|
(А.Н.Ремизов, 1987,стр.44-48, А.Н.Ремизов, 1999,стр.37-42, Н.Л.Лобоцкая,1978, стр. 363-371).
Математическая статистика - раздел прикладной математики, непосредственно примыкающий к теории вероятностей. Основное отличие математической статистики от теории вероятностей состоит в том, что в математической статистике рассматриваются не действия над законами распределения и числовыми характеристиками случайных величин, а приближенные методы отыскания этих законов и числовых характеристик по результатам экспериментов.
Основными понятиями математической статистики являются:
1. Генеральная совокупность;
2. выборка;
3. вариационный ряд;
4. полигон частот;
5. гистограмма.
Генеральная совокупность - большая статистическая совокупность, из которой отбирается часть объектов для исследования
(П р и м е р: все население области, студенты вузов данного города и т.д.)
Выборка (выборочная совокупность) - множество объектов, отобранных из генеральной совокупности.
Вариационный ряд - статистическое распределение, состоящее из вариант (значений случайной величины) и соответствующих им частот.
П р и м е р:
| X,кг | ||||||||||||
| m |
x - значение случайной величины (масса девочек в возрасте 10 лет);
m - частота встречаемости.
Используют дискретное (точечное) статистическое распределение и непрерывное (интервальное) статистическое распределение.
Для наглядности статистические распределения изображают графически в виде полигона частот или - гистограммы.
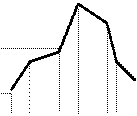
Полигон частот - ломаная линия, отрезки которой соединяют точки с координатами (x1,m1), (x2,m2),..., или для полигона относительных частот – с координатами (x1,р*1), (x2,р*2),...(Рис.1).
 |


 m mi/n f(x)
m mi/n f(x)
 | |||
 | |||
 x x
x x
Рис.1 Рис.2
Гистограмма частот - совокупность смежных прямоугольников, построенных на одной прямой линии (Рис.2), основания прямоугольников одинаковы и равны dx, а высоты равны отношению частоты к dx, или р* к dx (плотность вероятности).
|
|
|
П р и м е р:
| х, кг | 2,7 | 2,8 | 2,9 | 3,0 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | 4,0 | 4,1 | 4,2 | 4,3 | 4,4 |
| m |
Полигон частот

Отношение относительной частоты к ширине интервала носит название плотности вероятности f(x)=mi / n dx = p*i / dx
Oсновные этапы построения гистограммы.
Для объяснения используем данные предыдущего примера.
1. Расчет количества интервалов
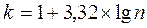
где n - число наблюдений. В нашем случае n = 100. Следовательно: 
2. Расчет ширины интервала dх:
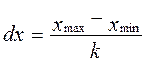 ,
, 
3. Составление интервального ряда:
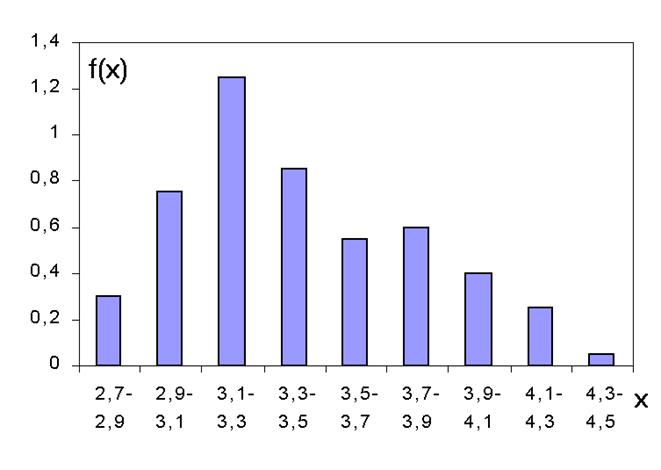
| dх | 2.7-2.9 | 2.9-3.1 | 3.1-3.3 | 3.3-3.5 | 3.5-3.7 | 3.7-3.9 | 3.9-4.1 | 4.1-4.3 | 4.3-4.5 |
| m | |||||||||
| f(x) | 0.3 | 0.75 | 1.25 | 0.85 | 0.55 | 0.6 | 0.4 | 0.25 | 0.05 |
Гистограмма
|
|
|


