Проверка статистических гипотез

(Лобоцкая Н.Л. 1978, стр.389-391, Лакин Г.Ф., стр.111-133)

Ни одно исследование не обходится без сравнений. Сравнивать приходится данные опыта с контролем, эффективность действия препаратов, продуктивность одной группы животных с продуктивностью другой и т.д.

Обычно, между сравниваемыми данными всегда имеются различия. Иногда различиями пренебрегают и утверждают, что, в целом, данные контрольной группы совпадают с данными опытной группы, другими словами различия между полученными данными недостоверны. В другом случае различиями пренебречь нельзя и в таком случае говорят, что различия между полученными данными достоверны. В каком случае делается тот или иной вывод?

Введём несколько основных понятий:

 

1. 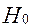- нулевая гипотеза, которая предполагает, что полученная в опыте разница между исследуемыми параметрами случайна;

2. - альтернативная гипотеза, которая противоречит нулевой и предполагает, что полученная в опыте разница между исследуемыми параметрами не случайна;

3. a - уровень значимости, равен вероятности ошибки, допускаемой при оценке принятой гипотезы (обычно равен 0,05; 0,01; 0,001).

 

Принять или отклонить гипотезу можно после её проверки. Для этих целей служит величина, называемая статистическим критерием или просто критерием.

Критерии, которые вычисляются по исходным данным (выборкам) t_ф (фактические критерии) с р а в н и в а ю т с я с табличными критериями t_кр.

 

ОСНОВНОЙ ПРИНЦИП проверки статистических гипотез сводится к следующему:

 

если фактически установленная величина tф превзойдёт или окажется равной критическому значению tкр, tф ³ tкр, то нулевую гипотезу отвергают. Если tф < tкр, принимают нулевую гипотезу.

 

 

ПАРАМЕТРИЧЕСКИЕ И НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ РАЗЛИЧИЯ

(Лакин Г.Ф., стр.111-133)

 

В биометрии применяют два вида статистических критериев:

1. п а р а м е т р и ч е с к и е;

2. н е п а р а м е т р и ч е с к и е.

Применение параметрических критериев для проверки статистических гипотез основано на предположении о нормальном распределении (закон Гаусса) совокупностей, из которых взяты сравниваемые выборки. К параметрическим критериям относятся: 1. критерий Стьюдента; 2. критерий Фишера.

Однако не всегда исходные данные подчиняются нормальному закону распределения. Кроме того, исходные данные могут быть представлены качественно (например, наличие или отсутствие боли, восприятие света - есть или нет и т.д.). В таком случае используют непараметрические критерии: например, критерий знаков. Хотя непараметрические критерии можно использовать и для нормально распределённых величин. Но при нормальном распределении признака параметрические критерии обладают большей мощностью, чем непараметрические.

 

КРИТЕРИЙ ЗНАКОВ

П р и м е р

 

Номера подопытных животных	Эозинофилия	Эффект воздействия
	До введения туберкулина	После введения туберкулина
1.	++	+	+
2.	+++	++	+
3.	++	+	+
4.	++	+	+
5.	+++	++	+
6.	++	+	+

Если разницы между признаками нет, ставят 0. Если есть разница - ставят “ + “ или “ - ” (“+“ если есть ожидаемый эффект). В нашем примере общее число наблюдений n = 15. Число случаев, давших ожидаемый эффект Z_ф = 13, общее число случаев без нулевых значений- Z = 14. Величину Z_ф = 13 сравнивают с Z_кр. (Z_кр определяют по таблице). В нашем примере Z_кр = 12 для Z = 14 и доверительной вероятности 0,05. Исходя из ОСНОВНОГО ПРИНЦИПА проверки статистических гипотез, имеем: Z_ф > Z_кр, значит нулевая гипотеза отвергается.

КРИТЕРИЙ СТЬЮДЕНТА

Для сравнения двух нормально распределенных совокупностей, у которых есть различия в средних выборочных значениях, используют критерий Стьюдента. Фактический критерий рассчитывают по формуле:

где - среднее значение первой выборочной совокупности;

- среднее значение второй выборочной совокупности;

- ошибка среднего для первой выборочной совокупности;

- ошибка среднего для второй выборочной совокупности.

Для вывода о достоверности различий между выборками используют ОСНОВНОЙ ПРИНЦИП проверки статистических гипотез. Нулевую гипотезу отвергают, если фактически установленная величина превзойдет или окажется равной критическому (стандартному) значению 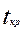этой величины для принятого уровня значимости a и числа степеней свободы k=n₁+n₂-2 (если объемы выборок одинаковы).

П р и м е р: При изучении влияния некоторой пищевой добавки на прирост массы животных были получены следующие значения. В первой группе животных =638 г, в контроле - =526 г. =402 и =382. Количество наблюдаемых животных в каждой группе было одинаковым: n₁=n₂ =9. Сделаем расчет: . В таблице критериев Стьюдента для k=n₁+n₂-2 =9±9-2=16 и уровня значимости a =0,05 находим 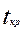=2,12. 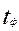> 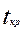, следовательно верна альтернативная гипотеза (пищевая добавка влияет на прирост массы животных, или, другими словами, полученная в эксперименте разница в показаниях статистически достоверна).

КРИТЕРИЙ ФИШЕРА

Для сравнения двух нормально распределенных совокупностей, у которых нет различий в средних выборочных значениях, но есть разница в дисперсиях, используют критерий Фишера. Фактический критерий рассчитывают по формуле:

где в числителе стоит большее значение выборочной дисперсии, а в знаменателе - меньшее. Для вывода о достоверности различий между выборками используют ОСНОВНОЙ ПРИНЦИП проверки статистических гипотез. Критические точки для содержатся в таблице. Нулевую гипотезу отвергают, если фактически установленная величина превзойдет или окажется равной критическому (стандартному) значению этой величины для принятого уровня значимости a и числа степеней свободы k₁=n_{большая}-1; k₂=n_{меньшая}-1.

П р и м е р: при изучении влияния некоторого препарата на скорость проростания семян было установлено, что в экспериментальной партии семян и контроле средняя скорость проростания одинакова, но есть разница в дисперсиях. =1250, 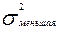=417. Объемы выборок одинаковы и равны 20. =2,12. Следовательно, нулевая гипотеза отвергается.

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: