 |
Тема 3. Обеспечение точности размерных цепей.
|
|
|
|
В изделии, изготовленном на предприятии размеры деталей находятся во взаимосвязи и взаимозависимости. Размерные связи детали или изделия анализируют с помощью теории размерных цепей.
Размерной цепью называется совокупность размеров, непосредственно участвующих в решении поставленной задачи и образующих замкнутый контур. Размеры, входящие в размерную цепь, называются звеньями. Звенья подразделяют на замыкающее (исходное) и составляющие. Среди составляющих различают увеличивающие и уменьшающие звенья.
Номинальный размер замыкающего звена А∆ может быть найден по формуле (7):
, (7)
где m – число звеньев размерной цепи;
m-1 – число составляющих звеньев;
n – число увеличивающих звеньев;
m-1-n – число уменьшающих звеньев;
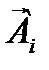- номинальный размер i-го увеличивающего звена;
- номинальный размер i-го уменьшающего звена.
Пример 1. По заданному чертежу вала построить размерную цепь и вычислить номинальный размер замыкающего звена.
Построение размерной цепи начнем с замыкающего звена ВΔ . Далее, следуя по ходу часовой стрелки находим размер 15-0,07 – он будет являться уменьшающим звеном, следовательно обозначим его как 
. Затем проводим линию 0-0, ограничивающую размеры вала, и от нее откладываем вправо размер 100+0,14 , который будет увеличивающим звеном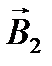 
. Далее проводим вторую ограничивающую линию 0-0 и влево от нее изображаем последний размер 45-0,062 , который будет уменьшающим звеном 
.
Номинальный размер замыкающего звена определим по формуле:
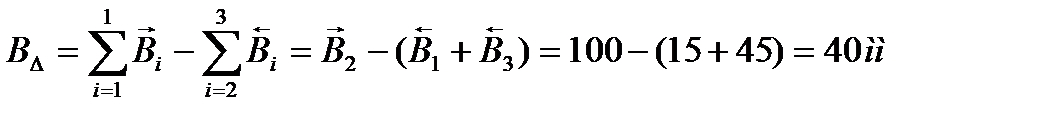
С помощью теории размерных цепей решают две основные задачи: прямую и обратную. При решении прямой задачи необходимо рассчитать допуски всех составляющих звеньев и назначить их предельные отклонения по заданным номинальным размерам всех звеньев, а также по известным предельным отклонениям исходного (замыкающего) звена.
|
|
|
При решении обратной задачи по известным значениям номинальных размеров и предельных отклонений всех составляющих звеньев размерной цепи требуется рассчитать номинальный размер замыкающего звена и его предельные (верхнее и нижнее) отклонения.
Верхнее и нижнее отклонение звена Bi размерной цепи можно вычислить по формулам (8):
Es(Bi) = Bi max - Bi ;
Ei(Bi) = Bi min - Bi , (8)
где Bi max (Bi min) – наибольший (наименьший) предельный размер i-го звена; Bi – номинальный размер i-го звена.
Для определения наибольшего и наименьшего размера замыкающего звена пользуются формулами (9):
(9)
,
где n – число увеличивающих звеньев; m-1-n – число уменьшающих звеньев; 
-номинальный размер i-го увеличивающего звена; 
- номинальный размер i-го уменьшающего звена.
Используя выведенные формулы, получим формулы для верхнего и нижнего отклонения замыкающего звена в общем виде (10, 11):
, (10)
где 
- верхнее отклонение i-го увеличивающего звена; 
- нижнее отклонение i-го уменьшающего звена.
, (11)
где 
- нижнее отклонение i-го увеличивающего звена; 
- верхнее отклонение i-го уменьшающего звена.
Соответственно, допуск замыкающего звена TBΔ:
TBΔ = Es(BΔ) – Ei(BΔ),
или в общем виде (12):
(12)
Пример 2. Решение обратной задачи методом полной взаимозаменяемости. При сборке изделия необходимо выдержать зазор в пределах 0,2..0,4мм. Необходимо провести расчет размерной цепи методом полной взаимозаменяемости и убедиться, что заданный зазор будет обеспечен после сборки деталей.
В данном случае необходимый зазор будет являться замыкающим звеном, размер 40+0,1 – увеличивающим звеном, а размер 
- уменьшающим звеном.
Найдем номинальный размер замыкающего звена:
Найдем верхнее и нижнее отклонение замыкающего звена:
Допуск замыкающего звена TCΔ будет равен:
|
|
|
TCΔ = Es(CΔ) – Ei(CΔ) = +0,43 – (+0,17) = 0,26 мм.
Определим предельные размеры замыкающего звена:
CΔ max = CΔ + Es(CΔ) = 0 + (+0,43) = 0,43 мм;
CΔ min = CΔ + Ei(CΔ) = 0 + (+0,17) = 0,17 мм.
Следовательно, при сборке деталей не будет обеспечено выполнение заданного зазора 0,2..0,4 мм, так как этот зазор может достигать значений 0,17..0,43 мм.
|
|
|
