 |
Понятие сигнала и его модели. Формы представления детерминированных сигналов.
|
|
|
|
Этапы обращения информации при использовании ее для выработки управляющих воздействий на объект.
Этапы обращения информации при использовании ее для выработки управляющих воздействий на объект.
При обращении в системах можно выделить отдельные этапы, т. к. материальным носителем информации является сигнал, то реально это будут этапы обращения и преобразования сигналов (рис. 1).
 |
На этапе восприятия информации осуществляется целенаправленное извлечение и анализ информации о каком-либо объекте (процессе), в результате чего формируется образ объекта, проводится его опознавание и оценка, отделяется интересующая нас информация от мешающей (шумов). Простейшим видом восприятия является различие двух противоположных состояний: наличия («да») и отсутствия («нет»), более сложным – измерение.
На этапе подготовки информации проводятся такие операции, как нормализация, аналого-цифровое преобразование, шифрование. В результате восприятия и подготовки получается сигнал в форме, удобной для передачи или обработки.
На этапах передачи и хранения информация пересылается из одного места в другое, либо от одного момента времени до другого. Поскольку теоретические задачи, возникающие на этих этапах, близки друг другу, этап хранения информации часто в самостоятельный не выделяется. При этом передача информации получает более широкое толкование. Для передачи на расстояние используются каналы различной физической природы: электрические, электромагнитные, оптические и др. Для хранения информации используются в основном полупроводниковые и магнитные носители (память). Извлечение сигнала на выходе канала, подверженного действию шумов носит характер вторичного восприятия.
|
|
|
На этапах обработки информации выделяются ее общие и существенные взаимозависимости, представляющие интерес для системы. Преобразование информации на этапе обработки (как и на других этапах) осуществляется либо средствами информационной техники, либо человеком (если процесс обработки не формализуем). В современных системах широко используются ЭВМ и микропроцессоры. В системах управления важнейшей целью обработки является решение задачи выбора управляющих воздействий (этап принятия решений).
Этап отображения информации должен предшествовать этапам, связанным с участием человека. Цель этапа отображения – представить человеку нужную ему информацию с помощью устройств, способных воздействовать на его органы чувств.
На этапе воздействия информации информация используется для осуществления необходимых изменений в системе.
Для справки дадим еще одно определение.
Совокупность средств информационной техники и людей, объединенных для достижения определенных целей или для управления, образуют автоматизированную информационную систему, к которой по мере надобности подключаются абоненты (люди или устройства), поставляющие и не использующие информацию.
Информационные системы, действующие без участия людей, называют автоматическими.
Понятие сигнала и его модели. Формы представления детерминированных сигналов.
В широком смысле слова под сигналом понимают материальный носитель информации: естественный или специально созданный.
В дальнейшем под сигналом будем понимать специально созданный сигнал для передачи сообщения в информационной системе.
Материальную основу сигнала составляет какой-либо физический объект или процесс, называемый носителем (переносчиком информации (сообщения)).
Носитель становится сигналом в процессе модуляции.
|
|
|
Параметры носителя, изменяемые во времени в соответствии с передаваемым сообщением, называют информационным.
В качестве носителя информации используются колебания различной природы, чаще всего гармонические, включая частный случай – постоянное состояние (w=0). В ИИС наибольшее распространение получили носители в виде электрического напряжения или тока. Поэтому, рассматривая в дальнейшем модели сигналов, для конкретности, будем соотносить их с электрическими сигналами.
Колебания принято подразделять на детерминированные и случайные.
Детерминированными называют колебания, которые точно определены в любые моменты времени.
Случайные колебания отличаются тем, что значения их некоторых параметров предсказать невозможно. Они могут рассматриваться как сигналы, когда несут интересующую нас информацию (случайные сигналы), или как помехи, когда мешают наблюдению интересующих нас сигналов.
При теоретическом изучении сигналов, исследовании их общих свойств мы отвлекаемся от их конкретной природы, содержания и назначения, заменяя моделями.
Модель – это выбранный способ описания объекта, процесса или явления, отражающий существенные с точки зрения решаемой задачи факторы.
Модель позволяет установить количественные соотношения между основными параметрами, характеризующими исследуемый объект или процесс (в нашем случае сигнал).
Методы математического моделирования многообразия.
Фундаментальные исследования базируются на методе аналитического моделирования, заключающимися в создании совокупности математических соотношений, позволяющих выявить зависимости между параметрами модели в общем виде. При этом широко используются модели, параметры которых противоречат физическим свойствам реальных объектов. Например, модель сигнала часто представляется суммой бесконечного числа функций, имеющих неограниченную продолжительность (синусоид). Поэтому важно обращать внимание на условие, при которых это не мешает получать результаты, соответствующие наблюдаемым в действительности.
Так как источник сообщений выдает каждое сообщение с некоторой вероятностью, то предсказать изменение значения информативного параметра невозможно. Следовательно, сигнал принципиально представляет собой случайное колебание и его аналитической моделью может быть только случайный процесс, определяемый вероятностными характеристиками.
|
|
|
Тем не менее, детерминированные колебания рассматривают и в этом случае говорят о детерминированном сигнале. Ему соответствует модель в виде функции, полностью определенной во времени.
Изучение моделей детерминированных сигналов необходимо по многим причинам. Важнейшая из них заключается в том, что результаты анализа детерминированных сигналов являются необходимыми для изучения более сложных случайных сигналов. Это обусловлено тем, что детерминированный сигнал может рассматриваться как элемент множества детерминированных функций, составляющих в совокупности случайный процесс, т.е. детерминированное колебание, представляет собой выраженную форму случайного процесса со значениями параметров, известными в любой момент времени с вероятностью, равной единице. Детерминированные сигналы имеют и самостоятельное значение. Они специально создаются для целей измерения, наладки и регулирования объектов информационной техники, выполняя роль эталонов.
Формы представления детерминированных сигналов.
В зависимости от структуры параметров сигналы подразделяют на дискретные, непрерывные и дискретно-непрерывные.
 |
В соответствии с этим существуют следующие разновидности математических представлений (моделей) детерминированного сигнала:
1) Непрерывная функция непрерывного аргумента (например, времени) (рис. 3, а);
2) Непрерывная функция дискретного аргумента, например, функция, значения которой отсчитывают только в определенные моменты времени (рис.3, б);
3) Дискретная функция непрерывного аргумента, например функция времени, квантованная по уровню (рис. 3, в);
4) Дискретная функция дискретного аргумента, например функция, принимающая одно из конечного множества возможных значений (уровней) в определенные моменты времени (рис. 3, г).
|
|
|
Для упрощения построения моделей сложные сигналы представляются совокупностью элементарных (базисных) функций, удобных для последующего анализа.
Наиболее широкий класс исследуемых систем – это инвариантные во времени линейные системы.
При анализе прохождения сложного сигнала u (t) через такие системы его представляют в виде взвешенной суммы базисных функций j k(t) (или соответствующего ей интеграла):
(1)
где [t1, t2] – интервал существования сигнала.
При выбранном наборе базисных функций сигнал u (t) полностью определяется совокупностью безразмерных коэффициентов С к. Такие совокупности чисел называют дискретными спектрами сигналов.
На интервале [t1, t 2] выражение (1) справедливо как для сигналов неограниченных во времени так и для сигналов конечной длительности. Однако за пределами интервала [ t 1,t2] сигнал конечной длительности не равен нулю, т.к. он представляется суммой в том случае, если условно считается периодически продолжающимся. Поэтому, когда для ограниченного во времени сигнала необходимо получить представление, справедливое для любого момента времени, используется интеграл
(2)
где j (a, t) – базисная функция с непрерывно меняющимся параметром a.
В этом случае имеется непрерывный сплошной спектр сигнала, который представляется спектральной плотностью S ( a ). Разрешимость ее обработки размерности a. Аналогом безразмерного коэффициента С к здесь является величина S (a)d a.
Совокупность методов представления сигналов в виде (1) и (2) называют обобщенной спектральной теорией сигналов. В рамках линейной теории спектра являются удобной формой представления сигналов.
Базисные функции j k(t) должны быть просты, обеспечивать быструю сходимость ряда (1) для любых сигналов u (t) и позволять легко вытенять значения коэффициентов С к. Базисные функции не обязательно должны быть действительными, их число может быть неограниченным (-¥ £ к £ ¥).
В случае практической аппроксимации реального сигнала совокупностью базисных сигналов решающее значение приобретает простота их технической реализации. Сигнал представляется суммой ограниченного числа (0 £ к £ n) действительных линейно независимых базисных функций (сигналов).
3. РЯДЫ ФУРЬЕ
Функциональный ряд 
(1)
называется тригонометрическим рядом; 
, 
и 
(
) – коэффициенты тригонометрического ряда.
Если ряд сходится, то его сумма есть периодическая функция 
с периодом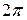 
, т.к. 
и 
являются периодическими с периодом .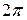
Таким образом 
.
Задача. Дана функция периодическая с периодом 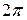. При каких условиях для можно найти тригонометрический ряд, сходящийся к данной функции?
|
|
|
Коэффициенты ряда Фурье
Периодическая с периодом 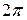функция такова, что она представляется тригонометрическим рядом, сходящимся к данной функции на интервале 
, т.е.
. (2)Коэффициенты , , равны
; (3) 
; (4) 
. (5)
Примеры разложения функций в ряд Фурье
Пример 1. Периодическая функция с периодом 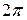определяется следующим образом:
, 
.
Эта функция кусочно-линейная и ограничена (рис. 1). Следовательно, она допускает разложение в ряд Фурье
Рисунок 1
По формуле (3) 
.
Применяя (4) и интегрируя по частям, найдем:
.
По (5) находим 
.
Таким образом, получаем ряд 
.
Это равенство имеет место во всех точках, кроме точек разрыва. В каждой точке разрыва сумма ряда равна среднему арифметическому ее пределов справа и слева, т.е. нулю.
|
|
|
