О разложении в ряд Фурье непериодических функци

 

Пусть на некотором отрезке задана кусочно монотонная функция (рис.8). Покажем, что данную функцию в точках ее непрерывности можно представить в виде суммы ряда Фурье. Для этого рассмотрим периодическую кусочно-монотонную функцию с периодом , совпадающую с функцией на отрезке .

Рисунок 8

 

Разложим в ряд Фурье. Сумма этого ряда во всех точках отрезка (кроме точек разрыва) совпадает с заданной функцией , т.е. мы разложили функцию в ряд Фурье на отрезке .

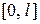Рассмотрим следующий важный случай. Пусть функция задана на отрезке . Дополняя определение этой функции произвольным отрезком на отрезке 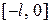(сохраняя кусочно монотонность), мы можем разложить эту функцию в ряд Фурье. В частности, если мы дополним определение этой функции тем, чтобы при было в результате получится четная функция (рис. 9).

Рисунок 9 Рисунок 10

 

В этом случае говорят, что функция “продолжается четным образом”. Эту функцию разлагают в ряд Фурье, который содержит только косинусы. Таким образом, заданную на отрезке 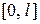функцию мы разложили по косинусам.

Если же мы продолжим определение функции при так: , то получим нечетную функцию, которая разлагается по синусам (рис. 10), т.е. функция “продолжается нечетным образом”. Таким образом, если на отрезке 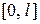задана некоторая кусочно монотонная функция , то ее можно разложить в ряд Фурье как по косинусам, так и по синусам.

 

 

4. Случайный процесс как модель сигнала.

 

Единственная то что определяемая во времени функция не может служить математической моделью сигнала при получении, передачи и преобразовании информации. Поскольку получение информации связано с устранением априорной неопределенности исходных состояний, однозначная функция времени только тогда будет нести информацию, когда она с определенной вероятностью выбрана из множества возможных функций. Поэтому в качестве моделей сигнала используется служебный процесс. Каждая выбранная детерминированная функция рассматривается как реализация этого случайного процесса.

Необходимо учитывать воздействие на полезный сигнал помех, которые по своей природе случайны. Математическая модель помехи представляется также в виде случайного процесса, параметры которого определяются экспериментально. Вероятностные свойства помехи, как правило, отличны от свойств полезного сигнала, что и лежит в основе методов их разделения.

Справка. Под случайным процессом (стохастическим) подразумевают такую случайную функцию времени U(t), значение которой в каждый момент времени случайны. Конкретный вид U(t) называют реализацией случайного процесса. Точно ее предсказать невозможно. Можно лишь определить статистические данные, характеризующие все множество конкретных реализаций, называемое ансамблем.

Основными признаками, по которым классифицируются случайные процессы, являются: пространство состояний, временной параметр и статистические зависимости между случайными величинами U(t_i) в разные моменты времени t_i.

Пространство состояний называют множество возможных значений случайной величины U(t_i). Случайный процесс, у которого множество состояний составляет континуум, а изменение состояний возможны в любые моменты времени, называют непрерывным случайным процессом.

Если же изменения состояний допускаются лишь в конечном или счетном числе моментов времени, то говорят о непрерывной случайной последовательности.

Случайный процесс с конечным множеством состояний, которые могут изменяться в произвольные моменты времени, называют дискретным случайным процессом. Если же изменения состояний возможны только в конечном или счетном числе моментов времени, то говорят о дискретных случайных последовательностях.

Примеры реализации указанных случайных процессов представлены на рис. 3.

В настоящее время чаще имеют дело с дискретными случайными последовательностями.

Среди случайных процессов с дискретным множеством состояний нас будут интересовать такие, у которых статистические зависимости распространяются на ограниченное число k следующих друг за другом значений. Они называются обобщенными Марковскими процессами k-го порядка.

5. Модуляция. Типы модуляции.

 

Модуляция

Процесс воздействия на носитель сообщения для изменения его параметров в целях создания сигнала, называют модуляцией.

Модуляция носителя сообщений, является необходимым условием передачи сведений о чем-либо, т.к. без модуляции не может возникнуть сигнал.

В современной технике передачи информации носителем сообщения, наиболее широко применяемым является электрический ток или напряжение. Для передачи информации используют постоянный, переменный синусоидальный и импульсный токи, вследствие чего способы модуляции имеют характерные особенности.

Постоянный ток. Постоянный ток (или напряжение) имеет только один параметр, который можно изменять, - силу тока (или напряжения), поэтому возможен только один способ модуляции постоянного тока – изменения его значения. Сигналы, создаваемые путем модуляции постоянного тока, являются непрерывными и используются для передачи информации о непрерывных величинах по рассмотренной ранее схеме (рис.1).

Переменный синусоидальный ток. (или напряжение)

(4)

характеризуется тремя параметрами: амплитудой U ₀, частотой f ₀ и фазой j ₀.

Формула (4) отражает закон изменения носителя информации – переменного напряжения – до начала его модуляции. (символы параметров фазы с индексом 0 (нуль)).

Изменения параметров переменного напряжения (одного или в комбинации) является его модуляцией и создает сигнал для передачи информации. Используют три вида модуляции синусоидального напряжения или тока: амплитудную, частотную и фазовую.

Амплитудная модуляция.

На рис. 4 приведен график, поясняющий процесс амплитудной модуляции.

Кривая u = u (t) дает закон изменения во времени носителя информации. До момента t ₁ (начала модуляций) и после момента t ₂ (конца модуляций) носитель изменяется по синусоидальному закону (4).

Кривая f (t) – закон изменения непрерывной величины, информацию о которой необходимо передать. Для этой цели необходимо иметь преобразователь, на выходе которого создавалось бы электрическое напряжение, изменяющееся по закону , где D U постоянная величина, не превышающая амплитуды носителя U ₀, k – множитель, выбираемый из условия kf (t) £ 1.

Рис. 4. Амплитудная модуляция синусоидальных колебаний.

 

Отношение называют глубиной модуляции.

Используя ту или иную электрическую схему, напряжением U воздействуют на амплитуду колебаний носителя сообщений так, чтобы она увеличилась или уменьшилась в зависимости от модуля и знака напряжения U. В результате получается, что носитель будет изменяться уже по закону

,

т.е. с амплитудой, изменяющейся во времени. Огибающая амплитуд носителя будут изменяться потому же закону, что и напряжение U, закон которого отличается от закона f (t) только масштабом числовых значений.

Модулированное по амплитуде переменное напряжение, пройдя канал связи, поступает на демодулятор в виде одно- или двухполупериодного выпрямителя с фильтром, на выходе которого получается постоянное напряжение, изменяющееся по тому же закону f (t), что и предмет сообщения.

Частота колебаний носителя должна быть больше частоты наивысшей гармонической составляющей процесса изменения во времени величины f (t), сведения о которой подлежат передаче.

Частотная модуляция.

Амплитуда гармонических колебаний при частотной модуляции остается неизменной, а частота изменяется по закону:

(5)

где D w - постоянная величина, не превышающая w ₀; k - множитель, выбираемый из условия kf (t)£1; f (t) – закон изменения во времени непрерывной величины, сообщение о которой нужно передать.

Мгновенное значение переменного синусоидального напряжения вместо обычной формы

можно представить в таком виде:

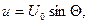(6)

где Q – мгновенное значение фазы.

Если частота постоянна, то если частота непостоянна, то Для синусоидального колебания, модулированного по частоте, (6) принимает вид

Подставляя сюда выражение для w из (5), получим

(7)

Приняв синусоидальное колебание, модулированное по частоте, получатель сообщения может изменить частоту частотомером. Показания прибора в этом случае будут изменяться по закону, представляемому формулой (5), т.е. отклонение частот от уровня w ₀ окажутся изменяющимися пропорционально f (t).

Модуляция по фазе.

При модуляции по фазе амплитуда и частота носителя постоянны, а мгновенная фаза колебания изменяется в соответствии с законом изменения предмета сообщения:

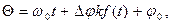
где D j - наибольшее отклонение мгновенной фазы от ее значения, определяемого слагаемым w ₀ t.

Величина D j <2 p и называется девиацией фазы. Коэффициент k, как и ранее выбирают из условия kf (t)£1.

Мгновенное значение напряжения, модулированного по фазе, выражается формулой

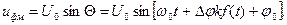
При амплитудной и частотной модуляции получатель может измерить амплитуду и частоту поступившего сообщения и указать, таким образом, числовое значение интересующей его величины f (t).

При модуляции по фазе нужно измерить мгновенную фазу Q, но это возможно только путем (сравнения) сопоставления фазы полученного переменного тока с фазой какого-то опорного переменного тока. Поэтому при модуляции по фазе по каналу связи приходится дополнительно передавать базовый переменный ток с мгновенной фазой . Разность 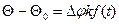можно измерить различными способами, и она будет однозначной функцией измеряемой величины f (t).

При всех трех рассмотренных видах модуляций синусоидальных колебаний – амплитудной, частотной и фазовой – изменяемый параметр делается непрерывной функцией тоже непрерывной величины, о которой необходимо передавать сообщение. Такую модуляцию называют непрерывной.

Импульсный ток.

На рис. 5 приведена диаграмма импульсного тока.

Рис. 5. Диаграмма импульсного тока и его параметры.

Из графика видно, что периодический импульсный ток имеет четыре параметра:

Амплитуду I_m, период Т, длительность (ширину) импульса t _u и мгновенную фазу Q.

Можно еще указать длительность (ширину) паузы t _п и частоту f, по f =1/ T, а t _п= T - t _u, т.е. эти величины зависимые. Отношение называют коэффициентом заполнения импульса, а обратную ему величину - скважностью импульсов.

При фазоимпульсной модуляции, как и при фазовой модуляции переменного тока, по каналу связи необходимо передавать одновременно с импульсом, несущими информацию, тактовые импульсы. Разность мгновенных фаз импульсов этих двух потоков будет однозначной функцией измеряемой величины.

Любой из параметров импульсного тока можно сделать непрерывной функцией той или иной непрерывной физической величины (предмета сообщения) и таким путем осуществить непрерывную модуляцию импульсного тока аналогично непрерывной модуляции синусоидального тока или напряжения. В зависимости от вида изменяемого параметра различают четыре вида непрерывной модуляции импульсного тока: амплитудно-импульсную, частотно-импульсную, фазоимпульсную и широтно-импульсную.

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: