Простая графическая интерполяция медианы и Q

На рис. 2 изображена зависимость вероятности р от длины сравниваемых линий по данным табл. 4. При достаточно большой выборке ответов данные обычно ложатся на 5-образную кривую. Меньшие по длине, чем стандарт, сравниваемые линии лишь изредка оце­ниваются как более длинные, а большие по длине - почти всегда оцениваются как более длинные. Точка, соответствующая на графике 63 мм (величина этало­на) показывает, в какой части проб эта длина при­знана большей при предъявлении ее второй в паре равных линий. Это типичный результат так называе­мой "отрицательной ошибки временной последова­тельности", ошибки, которая сама по себе представ­ляет очень интересную проблему из области восприя­тия. Соединив прямыми линиями точки, представ­ляющие данные эксперимента, мы проводим го­ризонтальные линии от оси ординат на уровне 25, 50 и 75% до пересечения с ломаной линией. А затем опускаем вертикальные линии из точек пересече­ния на абсциссу, чтобы определить физические ве­личины, соответствующие Q1, медиане Q2 и Q3, как это показано на рис. 2.

Рис. 2. Зависимость вероятности оценок "длин­нее" от длины линий, полученная методом постоян­ных раздражителей. Стандартный стимул - линия 63 мм. Подробности в тексте. Абсцисса - длина в мм. Ордината - вероятность оценки "длиннее". Первому квартилю (Q1) соответствует значение 61,2 мм, тре­тьему квартилю (Q3) - 63,6 мм, а медиане и точке субъективного равенства - 62,6 мм

Медиана (Мед.) - та длина линии, которая тео­ретически должна быть признана более длинной в одной половине проб и более короткой - в другой половине. В этом случае она является точкой субъек­тивного равенства (TCP), которую следует сравни­вать с физической величиной стандарта. При опре­делении точки субъективного равенства предпола­гается, что линия, соединяющая величины р, соот­ветствующие 62 и 63 мм, является в первом прибли­жении прямой. Однако, ошибка, связанная с этим, в зависимости от области приложения результатов, может не иметь серьезных последствий. В данном при­мере точка субъективного равенства или пятидеся­типроцентный уровень равен примерно 62,5мм. Само собой разумеется, что алгебраическое определение медианы также возможно и дает следующие резуль­таты:

,
где 0,34 является полученным в эксперименте значением р, соответствующим 62 мм и лежащим непосредственно ниже искомого значения р, равно­го 0,50; а 0,59 соответствует 63 мм и лежит непосред­ственно выше искомого р.

Обратите внимание, что полученное значение стимула, соответствующее р = 0,50, является тем же самым, что и при графической интерполяции. Это и понятно: обе величины являются лишь приближе­ниями, зависящими от сделанного выше допуще­ния о линейности. Как и следовало ожидать от этих оценок, точка субъективного равенства, полученная обоими методами, близка к эталону. Однако пяти­десятипроцентный уровень обычно не представляет большего интереса; только в опытах по измерению абсолютного порога наиболее важна эта точка, как соответствующая значению абсолютного порога. В данном опыте по определению разностного порога нужна мера вариабельности или неопределенности, а полуинтерквартильный диапазон, Q, является наи­более ценным в данном методе анализа.

,
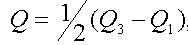где Q3 и Q1 - длины линий, соответствующие значениям р = 0,75 и р - 0,25 и полученные при помощи линейной интерполяции.

В нашем примере

Эта мера вариабельности используется как по­казатель различительной чувствительности или раз­ностный порог, но численно она не равна разностному порогу, измеренному, например, методом границ, хотя и сходна с разностным порогом, опре­деленным как половина интервала неопределеннос­ти (DL = ИН/2). Если допустить, что распределение частот оценок является нормальным, то можно вос­пользоваться средним квадратическим отклонением как мерой разностного порога в соответствии с урав­нением

s = 1,483Q

Для данных табл. 4:

s = 1,483x1,2 = 1,8.

Среднее квадратическое отклонение имеет хо­рошо известные и полезные свойства и, несомнен­но, прямое определение его было бы лучшим методом. Итак, среднее арифметическое надежнее и пред­почтительнее, чем медиана, если предполагается, что распределение оценок нормально.

Рубинштейн ОСНОВЫ ОБЩЕЙ ПСИХОЛОГИИ. / Составители, авторы комментариев и послесловия
А.В.Брушлинский, К.А.Абульханова-Славская. Глава VII