 |
Графический интерфейс пользователя MATLAB
|
|
|
|
Лабораторная работа №1
ГРАФИЧЕСКИЙ ИНТЕРФЕЙС ПОЛЬЗОВАТЕЛЯ И ПРОСТЕЙШИЕ ВЫЧИСЛЕНИЯ
Цели работы:
1. Знакомство с интерфейсом пакета MATLAB и основными положениями.
2. Знакомство с простыми типами данных, вводом данных и визуализацией результата вычислений.
3. Получение практических навыков работы в диалоговом режиме.
4. Работа с комплексными числами и комплексными функциями.
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
MATLAB – это высокопроизводительный язык для технических расчётов. Он включает в себя вычисления, визуализацию и программирование в удобной среде, где задачи и решения выражаются в форме, близкой к математической. Типичное использование MATLAB – это:
– математические вычисления;
– создание алгоритмов;
– моделирование;
– анализ данных, исследования и визуализация;
– научная и инженерная графика;
– разработка приложений, включая создание графического интерфейса.
Графический интерфейс пользователя MATLAB
Графический интерфейс пользователя MATLAB состоит из 4-х независимых окон, имеющих следующие названия: Workspace, Command Window,Command History, Current Director (рис. 1).

Рис. 1. Графический интерфейс пользователя пакета MATLAB
Окно Workspace (браузер рабочей области) используется для отображения состояния зарезервированной области памяти компьютера, в которой хранятся переменные, используемые в данном сеансе работы.
Окно Command Window является основным окном, в котором вводятся исполняемые команды и отображаются результаты вычислений.
Окно Command History используется для отображения содержимого буфера, в котором хранятся выполненные ранее команды пакета.
В окне Current Directory отображается список файлов и вложенных папок активного в данный момент каталога.
|
|
|
Для управления окнами используются стандартные средства операционной системы Windows. Для закрытия окон, отображение которых представляется пользователю в данный момент нецелесообразным, используется команды меню View. Наиболее удобна для работы форма графического интерфейса, когда на экране компьютера одновременно отображены окна
Command Window, Command Histor, иногда окно Workspace.
2. Структура окна Command Window
2.1. Главное окно
После запуска MATLAB на экране монитора мы видим окно Command Window (главное окно), содержащее: меню, инструментальную линейку с кнопками, клиентскую часть окна со знаком приглашения. Это окно обычно называется командное окно системы МАТLAB, его структура аналогична структуре Windows-приложений (рис. 2). Здесь происходят вычисления, и мы видим приглашение >>.
2.2. Зона просмотра и зона редактирования
Командное окно MATLAB разделено на две принципиально различных зоны: зону просмотра и зону редактирования (рис. 2).

Рис. 2. Структура командного окна MATLAB
Исправление информации в зоне просмотра невозможно. В зоне просмотра, можно с помощью мыши выделить любой фрагмент текста, затем скопировать его в буфер обмена операционной системы Windows, затем вставить данный фрагмент в командную строку MATLAB или документ, созданный в каком-либо приложении, работающем под управлением операционной системы Windows.
2.2. Понятие сессии
Сеанс работы с МАТLAB принято называть сессией (session). Сессия – это текущий документ, отражающий работу пользователя с системой. В ней имеются строки ввода, вывода, сообщения об ошибках. Входящие в сессию определения переменных и функций, расположенные в рабочей области памяти (но не саму сессию) можно записать на диск (файлы с расширением MAT), используя команду SAVE.
2.3. О переносе строки в сессии
В некоторых случаях вводимое математическое выражение может оказаться настолько длинным, что для него не хватит одной строки. В этом случае часть выражения можно перенести на новую строку с помощью знака многоточия..., то есть три или более точек (рис. 3).
|
|
|
Этот приём может быть полезен для создания наглядных документов, у которых предотвращается заход строк в невидимую область окна.
Максимальное число символов в одной строке — 4096 (в ранних версиях оно ограничивалось 256), но со столь длинными строками работать неудобно.

Рис. 3. Ввод команды, размещающейся на нескольких логических строках ввода
Очистка командного окна MATLAB осуществляется командой clc, которая, однако, оставляет неизменным содержимое буфера команд и рабочего пространства MATLAB. Действительно, если после этого набрать имя ранее вычисленной переменной d, то после нажатия клавиши ENTER мы снова увидим её значение:
>> d
d =
28. 8496
3. Браузер рабочей области – окно Workspace.
Значения переменных, вычисленных в течение текущего сеанса работы, сохраняются в специально зарезервированной области оперативной памяти компьютера, называемой рабочим пространством MATLAB (браузером рабочей области MATLAB – окно Workspace), которое мы видим на рис. 4.

Рис. 4. Окно просмотра рабочей области памяти
Браузер рабочей области служит для просмотра рабочей области памяти. Для вызова браузера в командном окне надо набрать: DesktopWorkspase.
3.1. Возможности браузера
Браузер позволяет:
Ø просмотреть существующие в памяти объекты;
Ø редактировать их содержимое;
Ø удалять объекты из памяти, т.к. матрицы и графики могут занимать многие мегабайты (выделить нужное и delete);
Ø векторы и матрицы могут занимать большой объем памяти, цветные изображения с высоким разрешением, могут занимать в памяти объем, исчисляемый многими мегабайтами, и в этом случае оценка их размера становится необходимой.
Для вывода содержимого объекта достаточно выделить его имя с помощью мыши и щёлкнуть па кнопке Open. Объект можно открыть и двойным щелчком на его имени в списке. Кнопка Delete уничтожает объект с заданным именем и удаляет его из памяти, а кнопка Close закрывает окно просмотра.
3.2. Окно Array Editor
Из окна Workspase двойным щелчком левой кнопки мыши по строке, содержащей имя переменной, можно вызвать окно Array Editor, в котором можно просматривать и менять значения выбранной переменной. Для примера на рис. 5. показано соответствующее окно, появившееся после двойного клика по строке, содержащей имя переменной а.
|
|
|
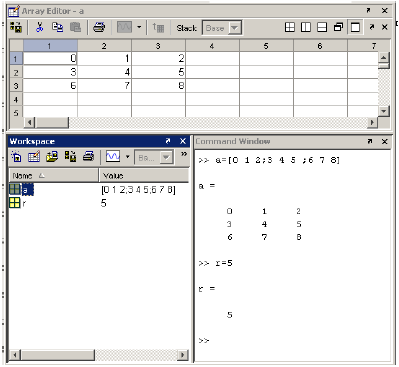
Рис. 5. Три окна – Сcommand Window, Workspace и Array Editor
4. Интерфейс редактора М-файлов
Для подготовки, редактирования и отладки m-файлов служит специальный многооконный редактор. Он выполнен как типичное приложение Windows (рис. 6).
Редактор М-файлов можно вызвать командой Edit из командной строки или командой File> New >M-file.

Рис. 6. Интерфейс редактора М-файлов
После этого в окне редактора можно:
– создавать свой файл,
– пользоваться средствами его отладки и запускать свой файл, используя команду Save As меню File редактора.
На первый взгляд может показаться, что редактор/отладчик – просто лишнее звено в цепочке «пользователь – MATLAB». И в самом деле, текст файла можно было бы ввести в окно системы и получить тот же результат.
Однако на деле редактор/отладчик выполняет важную роль. Он позволяет создать m-файл (программу) без многочисленной ненужной информации, которая сопровождает работу в командном режиме. Редактор обеспечивает синтаксический контроль файла.
4.1. Отладочные средства редактора
Редактор имеет и другие важные отладочные средства:
– он позволяет устанавливать в тексте файла специальные метки, именуемые точками прерывания (останова). При их достижении вычисления приостанавливаются, и пользователь может оценить промежуточные результаты вычислений (например, значения переменных), проверить правильность выполнения циклов и т. д.;
– редактор позволяет записать файл в текстовом формате и сохранить ваш файл.
4.2. Отображение имён переменных из рабочего пространства
Для отображения имён переменных, размещённых в данный момент в рабочем пространстве, нужно выполнить команду who. Данная команда отображает в рабочем окне список всех переменных, находящихся в рабочем пространстве MATLAB. Выполнив команды, представленные на рис. 6, и далее команду
|
|
|
>> who
получим
Your variables are:
x y
>>
4.3. Сохранения в файле содержимого рабочего пространства
После завершения сеанса работы с MATLAB все ранее вычисленные переменные теряются. Для сохранения в файле на диске компьютера содержимого рабочего пространства, нужно выполнить команду меню File Save Workspace as...
После чего появляется стандартное диалоговое окно операционной системы Windows для выбора каталога на диске и имени файла. Для файлов, в которых MATLAB сохраняет значения переменных из рабочего пространства нужно использоваться расширение mat, поэтому такие файлы принято называть «МАТ-файлами».
4.4. Цветовые выделения и синтаксический контроль
Редактор/отладчик m-файлов выполняет синтаксический контроль программного кода по мере ввода текста. При этом используются следующие цветовые выделения:
– ключевые слова языка программирования – синий цвет;
– операторы, константы и переменные – чёрный цвет;
– комментарии после знака % – зелёный цвет;
– символьные переменные (в апострофах) – зелёный цвет;
– синтаксические ошибки – красный цвет.
Благодаря цветовым выделениям вероятность синтаксических ошибок резко снижается. Однако далеко не все ошибки диагностируются. Ошибки, связанные с неверным применением операторов или функций (например, применение оператора – вместо + или функции cos(x) вместо sin(x) и т. д.), не способна обнаружить ни одна система программирования. Устранение такого рода ошибок – дело пользователя, отлаживающего свои алгоритмы и программы.
5. MATLAB в роли суперкалькулятора.
Система MATLAB создана таким образом, что любые (подчас весьма сложные) вычисления можно выполнять в режиме прямых вычислений, то есть без подготовки программы. Режим работы с MATLAB, в котором пользователь вводит команды в командной строке, задавая математические выражения или обращаясь к функциям MATLAB, называется интерактивным режимом.
Это превращает MATLAB в необычайно мощный калькулятор, который способен производить не только обычные для калькуляторов вычисления например:
– выполнять арифметические операции и вычислять элементарные функции);
– операции с векторами и матрицами;
– комплексными числами;
– рядами и полиномами;
– задать и вывести графики различных функций от простой синусоиды до сложной трёхмерной фигуры.
5.1. Некоторые основные положения
Работа с системой в режиме прямых вычислений носит диалоговый характер и происходит по правилу «задал вопрос, получил ответ ». Пользователь набирает на клавиатуре вычисляемое выражение, редактирует его (если нужно) в командной строке и завершает ввод нажатием клавиши <Enter>.
|
|
|
Ø >> – служит для указания ввода исходных данных;
Ø данные вводятся с помощью простейшего строчного редактора;
Ø; – точка с запятой отделяет строки матриц, а точка с запятой в конце оператора (команды) отменяет вывод результата на экран;
Ø [ ] – квадратные скобки используют для создания матриц и векторов;
Ø – пробел служит для разделения элементов матриц;
Ø, – запятая применяется для разделения элементов матриц и операторов в строке ввода;
Ø: – двоеточие используется для указания диапазона (интервала изменения величины) и в качестве знака групповой операции над элементами матриц;
Ø! – отмечает начало команды DOS;
Ø ’ – апостроф указывает на символьные строки;
Ø % – знак процента обозначает начало комментария;
Ø ans – служебная переменная MATLAB, которой присваивается результат последнего вычисления;
Ø = - знак присваивания;
Ø встроенные функции (например, sin и другие) записываются строчными буквами и их аргументы указываются в круглых скобках;
Ø результат вычислений выводится в строках вывода (без знака >>).
5.2. Ориентация на матричные операции.
Напомним, что двумерный массив чисел или математических выражений принято называть матрицей, а одномерный массив называют вектором (рис. 7).
Векторы и матрицы характеризуются размерностью и размером. Размерность определяет структурную организацию массивов в виде
– строки (размерность 1);
– страницы (размерность 2);
– куба (размерность 3) и т. д.
Так что вектор является одномерным массивом, а матрица представляет собой двумерный массив с размерностью 2.
MATLAB допускает задание и использование многомерных массивов, но мы пока ограничимся только одномерными и двумерными массивами – векторами и матрицами.
Размер вектора – это число его элементов. Размер матрицы определяется числом её строк т и столбцов п. Обычно размер матрицы указывают как m x n.
Матрица называется квадратной, если т = n, то есть число строк матрицы равно числу её столбцов.
Векторы и матрицы могут иметь имена, например V – вектор или М – матрица. Элементы векторов и матриц рассматриваются как индексированные переменные, например:
– V(2) – второй элемент вектора V;
– М(23) – третий элемент второй строки матрицы М.
| a | c | w | |||||||||||||||||
| а | б | u | j | i | b | ||||||||||||||
| е | |||||||||||||||||||
| в | |||||||||||||||||||
| г |
Рис. 7. Примеры векторов и матриц
а - столбец, б- строка, в- прямоугольная матрица, г - квадратная матрица, е - матрица единичной размерности (простая переменная).
Система MATLAB выполняет сложные и трудоёмкие операции над векторами и матрицами даже в режиме прямых вычислений без какого-либо программирования. Ею можно пользоваться как мощнейшим калькулятором, в котором наряду с обычными арифметическими и алгебраическими действиями могут использоваться такие сложные операции как:
Ø инвертирование матрицы;
Ø вычисление её собственных значений;
Ø решение системы линейных уравнений;
Ø вывод графиков функций и т.д.
5.3. Действия над матрицами
5.3.1. Ввод вектора
Две записи для вектора – V = [l 2 3 4] и V = [l, 2, 3, 4] – являются идентичными. Список заключается в квадратные скобки. Для выделения п -го элемента вектора V используется выражение V(n). Оно задаёт соответствующую индексированную переменную.
5.3.2 Ввод матрицы
Матрица задаётся в виде ряда векторов, представляющих е` строки и заключённых в квадратные скобки. Для разделения элементов векторов используется пробел или запятая, а для отделения одного вектора от другого – точка с запятой. Для выделения отдельного элемента матрицы М используется выражение вида M(j,i), где М – имя матрицы, j – номер строки и i – номер столбца.
Для ввода матрицы нужно:
>> М = [l, 2; 4, 5] или
>> М = [l, 2; 4, 5] или
>> М = [l, 2 <ENTER>
4 5] <ENTER>
M =
1 2
4 5
>> M (2,1) – индексированная переменная
ans=
5.3.3. Выполнение простых векторных операций
В примере, рассмотренном ниже, задан четырёхэлементный вектор V со значениями элементов 1, 2, 3 и 4. Далее вычисляются функции синуса и экспоненты с аргументом в виде вектора, а не скаляра.
>> u = [1 2 3 4]
u =
1 2 3 4
>> sin(u)
ans =
0.8415 0.9093 0.1411 -0.7568
>> exp(u)
ans =
2.7183 7.3891 20.0855 54.5982
>> u*3
ans =
3 6 9 12
>> u.^2
ans =
1 4 9 16
В языках программирования высокого уровня вычисления с массивами осуществляются поэлементно, поэтому в соответствующих процедурах приходится программировать вычисление выражений для каждого элемента массива. В MATLAB этого не требуется, так как в М-языке имеются групповые операции, выполняемые сразу над всем массивом. В частности, в М-языке MATLAB можно производить групповые вычисления над массивами, используя обычные математические функции, которые в традиционных языках программирования работают только со скалярными аргументами. Например, для вычисления таблицы значений функции косинус в равноотстоящих точках отрезка [0; π/2], отстоящих друг от друга на расстоянии 0,01 достаточно использовать всего две команды
>> х = 0:0.01: pi / 2;
>> y = cos (х);
>> whos x у
Name Size Bytes Class
x 1x158 1264 double array
у 1x158 1264 double array
Grand total is 316 elements using 2528 bytes
Аналогично вычисляются функции от двумерных массивов:
>> b= [0 pi / 6; pi / 4 pi / 2; 5 * pi / 6 3 * pi / 4]
b =
0 0.5236
0.7854 1.5708
2.6180 2.3562
>> sin (b)
ans =
0 0.5000
0.7071 1.0000
0.5000 0.7071
5.3.4 Создание матриц
Простейшей операций с матрицей является её создание. Для создания строки необходимо указать его имя, знак равенства и в квадратных скобках через запятую или через пробел перечислить значения элементов:
>> А=[1 2 3 4 5];
В случае если необходимо создать столбец чисел, то в качестве разделителя выступает символ точка с запятой:
>> B=[1; 3; 5; 7];
Для создания квадратной или прямоугольной матрицы понадобится чередовать оба этих способа.
>> С=[1 2 3; 4 5 6; 7 8 9];
5.3.5 Создание матриц специального вида.
Для генерации векторов пользователю предоставляется следующая команда: <Имя вектора>=<Начальное значение>:<Шаг>:<Конечное значение>
>> Х=6: 0.2: 26;
В результате получиться вектор X следующего вида:
| 6.2 | 6.4 | 6.6 | … | 25.6 | 25.8 |
В математике часто встречаются матрицы специального вида. Ниже приведён ряд из них:
Единичная матрица, рис. 8.а. В единичной матрице все элементы равны нулю, кроме элементов стоящих на главной диагонали (матрица является квадратной). Для создания единичной матрицы Вам необходимо подать команду <Имя матрицы>=eye(<Размер>);
>> a = eye(4);
Матрица со всеми единицами, рис. 8б. Эта матрица содержит единицы во всех ячейках. Для создания матрицы необходимо указать <Имя матрицы>= ones (<Кол-во строк>, <Кол-во столбцов>);
>> b = ones(3, 4);
Нулевая матрица, рис. 8в. Эта матрица содержит во всех своих ячейках одни нули. Для создания необходимо выполнить следующую команду: <Имя матрицы>= zeros (<Кол-во строк>, <Кол-во столбцов>);
>> c =zeros(4, 2);
Случайная матрица, рис. 8г. Все значения этой матрицы получаются с генератора случайных чисел. Для создания такой матрицы необходимо дать следующую команду: <Имя матрицы>=rand(<Кол-во строк>, <Кол-во столбцов>);
>> d =rand(3, 4);
| а | б | в | г |
Рис. 8. Специальные матрицы.
5.3.6 Доступ к ячейкам матрицы.
Для доступа к ячейкам матрицы необходимо указать имя матрицы, номер строки и номер столбца. Нумерация строк и столбцов ведётся с ЕДИНИЦЫ! Номера пишутся в круглых скобках. Общий формат записи: <Имя массива>(<Номер строки>, <Номер столбца>);
>> d(3,2)
ans =
>> d(3,1) = 9;
>> d
ans =
5 6
4 1
9 3
5.3.7 Умножение, деление матрицы на скаляр.
В математики для всех матриц определена операция умножения (деления) матрицы на скаляр (число) – «.*» («./»). Все значения матрицы в этом случае умножаются (делятся) на это число.
| A(1,1) | A(1,2) | A(1,3) | A(1,1).*r | A(1,2).*r | A(1,3).*r | |||
| A(2,1) | A(2,2) | A(2,3) | .* | r | = | A(2,1).*r | A(2,2).*r | A(2,3).*r |
| A(3,1) | A(3,2) | A(3,3) | A(3,1).*r | A(3,2).*r | A(3,3).*r |
5.3.8 Сложение, вычитание скаляра из матрицы.
Кроме операции умножения матрицы на скаляр, для матрицы и скаляра определены операции сложение «+» и вычитания «–». Действия так же выполняются с каждой ячейкой матрицы отдельно.
5.3.9 Сложение, вычитание матриц.
Эта операция допустима только с матрицами одинакового размера. При выполнении операции действие выполняется с соответствующими друг другу ячейками. Пример:
| а(1,1) | а(1,2) | а(1,3) | b(1,1) | b(1,2) | b(1,3) | а(1,1)+ b(1,1) | а(1,2)+ b(1,2) | а(1,3)+ b(1,3) | ||
| а(2,1) | а(2,2) | а(2,3) | + | b(2,1) | b(2,2) | b(2,3) | = | а(2,1)+ b(2,1) | а(2,2)+ b(2,2) | а(2,3)+ b(2,3) |
| а(3,1) | а(3,2) | а(3,3) | b(3,1) | b(3,2) | b(3,3) | а(3,1)+ b(3,1) | а(3,2)+ b(3,2) | а(3,3)+ b(3,3) |
5.3.10 Произведение матриц.
При выполнении операции перемножения матриц выполняется последовательное умножение строки на столбец. При этом количество столбцов в первой матрице должно равняться количеству строк во второй матрице. Матрица результата будет иметь столько же строк, сколько и в первой матрице, и количество столбцов равное количеству столбцов во второй матрице.
| A(1,1) | A(1,2) | A(1,3) | B(1,1) | B(1,2) | A(1,1)*B(1,1)+ A(1,2)*B(2,1)+ A(1,3)*B(3,1) | A(1,1)*B(1,2)+ A(1,2)*B(2,2)+ A(1,3)*B(3,2) | ||
| A(2,1) | A(2,2) | A(2,3) | * | B(2,1) | B(2,2) | = | A(2,1)*B(1,1)+ A(2,2)*B(2,1)+ A(2,3)*B(3,1) | A(2,1)*B(1,2)+ A(2,2)*B(2,2)+ A(2,3)*B(3,2) |
| B(3,1) | B(3,1) |
6. Основные объекты MATLAB
6.1. Понятие о математическом выражении
Центральным понятием всех математических систем является математическое выражение. Оно задаёт то, что должно быть вычислено в численном (реже символьном) виде. Вот примеры простых математических выражений:
2 + 3
2.301 * sin (x ^ 2)
4 + ехр (3) / 5
sqrt (y) /2
sin (pi /2)
Математические выражения строятся на основе:
Ø чисел;
Ø констант;
Ø переменных;
Ø операторов,
Ø функций и разных спецзнаков.
Далее даются краткие пояснения о сути этих понятий.
6.2. Действительные числа
Число – простейший объект языка MATLAB, представляющий количественные данные. Числа можно считать константами, имена которых совпадают с их значениями. Числа могут быть:
Ø целыми;
Ø дробными;
Ø с фиксированной точкой;
Ø плавающей точкой (научном формате с указанием мантиссы и порядка числа).
Ниже приводятся примеры представления чисел:
-3
2.301
0.00001
123.456 е - 24
- 234.456 е 10
6.2.1. Основное при работе с числами
Ø в мантиссе чисел целая часть отделяется от дробной точкой,
Ø для отделения порядка числа от мантиссы используется символ е, – знак «плюс» у чисел не проставляется, а знак «минус» у числа называют унарным минусом.
Ø пробелы между символами в числах не допускаются,
Ø ввод чисел возможен в любом удобном для пользователя виде,
Ø вычисления происходят в формате с двойной точностью,
Ø для установки формата используется команда format. задание формата сказывается только при выводе чисел.
|
|
|
12 |


