 |
В MATLAB не принято делить числа на целые и дробные, короткие и длинные и так далее, как это принято в большинстве языков программирования, хотя задавать числа в таких формах можно.
|
|
|
|
Операции над числами выполняются всегда в формате с двойной точностью. Такой формат удовлетворяет подавляющему большинству требований к численным расчётам, но совершенно не подходит для символьных вычислений с произвольной (абсолютной) точностью. Символьные вычисления MATLAB может выполнять с помощью специального пакета расширения Symbolic Math Toolbox.
7. Константы и системные переменные
Константа – это предварительно определённое числовое или символьное значение, представленное уникальным именем. Числа (например, 1, -2 и 1.23) являются безымянными числовыми константами.
Другие виды констант в MATLAB принято называть системными переменными, поскольку, с одной стороны, они задаются системой при её загрузке, а с другой — могут переопределяться.
7.1. Основные системные переменные, применяемые в системе MATLAB
– i или j – мнимая единица (корень квадратный из -1);
– pi -число π = 3.1415926...;
– eps – погрешность для операций над числами с плавающей точкой (2-52);
– realmin – наименьшее число с плавающей точкой (2 -1022);
– realmax – наибольшее число с плавающей точкой (21023);
– inf – значение машинной бесконечности;
– ans – переменная, хранящая результат последней операции и обычно вызывающая его отображение на экране дисплея;
– NaN – указание на нечисловой характер данных (Not-a-Number).
Вот примеры применения системных переменных:
>> 2 * pi
ans =
6.2832
>> eps
ans =
2.2204 е - 016
>> realmin
ans =
2.2251e - 308
>> realmax
ans =
1.7977 e + 308
>> 1 / 0
Warning: Divide by zero,
ans =
Inf
>> 0 / 0
Warning: Divide by zero,
ans =
NaN
7.1.1. Основные положения для системных переменных
Ø как отмечалось, системные переменные могут переопределяться. Можно задать системной переменной eps иное значение, например eps = 0.0001;
|
|
|
Ø однако важно то, что их значения по умолчанию задаются сразу после загрузки системы;
Ø поэтому неопределёнными, в отличие от обычных переменных, системные переменные не могут быть никогда.
7.2. Символьная константа
Символьная константа – это цепочка символов, заключённых в апострофы, например:
' Hellо my friend! '
' Привет '
' 2 + 3 '
Если в апострофы помещено математическое выражение, то оно не вычисляется и рассматривается просто как цепочка символов. Так что ' 2 + 3 ' не будет возвращать число 5.
Однако с помощью специальных функций преобразования символьные выражения могут быть преобразованы в вычисляемые. Соответствующие функции преобразования будут рассмотрены в дальнейшем. Символьные вычисления MATLAB может выполнять с помощью специального пакета расширения Symbolic Math Toolbox.
8. Текстовые комментарии
Поскольку MATLAB используется для достаточно сложных вычислений, важное значение имеет наглядность их описания. Она достигается, в частности, с помощью текстовых комментариев. Текстовые комментарии вводятся с помощью символа % в начале строки:
% Комментарий
9. Переменные и присваивание им значений
Переменные – это имеющие имена объекты, способные хранить некоторые данные. В зависимости от этих данных переменные могут быть
– числовыми или символьными;
– векторными или матричными.
В системе MATLAB можно задавать переменным определённые значения. Для этого используется операция присваивания, вводимая знаком равенства:
Имя переменной = Выражение
Типы переменных заранее не декларируются. Они определяются выражением, значение которого присваивается переменной. Так, если это выражение – вектор или матрица, то переменная будет векторной или матричной.
9.1. Имя переменной (идентификатор)
Ø может содержать сколько угодно символов, но запоминается и идентифицируется только 31 начальный символ.
|
|
|
Ø имя любой переменной не должно совпадать с именами других переменных, функций и процедур системы, то есть оно должно быть уникальным.
Ø имя должно начинаться с буквы, может содержать буквы, цифры и символ подчёркивания _ недопустимо включать в имена переменных пробелы и специальные знаки, например +, -, *, / и т. д., поскольку в этом случае правильная интерпретация выражений становится невозможной.
Ø желательно использовать для обозначений переменных содержательные имена, например speed_l для переменной, обозначающей скорость первого объекта.
Ø переменные могут быть обычными и индексированными, то есть элементами векторов или матриц;
Ø могут использоваться и символьные переменные, причём символьные значения заключаются в апострофы, например s='Demo'.
9.2. Уничтожение определений переменных
Как мы уже рассматривали, в памяти компьютера переменные занимают определённое место, называемое рабочим пространством (workspace). Для очистки рабочего пространства используется функция clear в разных формах, например:
– clear – уничтожение определений всех переменных;
– clear х – уничтожение определения переменной х;
– clear a, b, с – уничтожение определений нескольких переменных.
Уничтоженная (стёртая в рабочем пространстве) переменная становится неопределённой. Использовать такие переменные нельзя, и такие попытки будут сопровождаться выдачей сообщений об ошибке.
10. Операторы и функции
Оператор – это специальное обозначение для определённой операции над данными – операндами. Например, простейшими арифметическими операторами являются знаки суммы (+), вычитания (–), умножения (*) и деления (/).
Операторы используются совместно с операндами. Например, в выражении 2+3 знак + является оператором сложения, а числа 2 и 3 – операндами.
Следует отметить, что большинство операторов относится к матричным операциям, что может служить причиной серьёзных недоразумений.
Например, операторы умножения (*) деления (/)ивозведения в степень(^) вычисляют произведение, частное от деления и возведение в степень двух массивов, векторов или матриц. Есть ряд специальных операторов, например оператор (\) означает деление справа налево, а операторы (.*) (./)и(.^) означают почленное умножение, деление и возведение в степень массивов.
|
|
|
Следующие примеры поясняют сказанное на примере операций с векторами:
>> V1 = [2 4 6 8]
V1 =
2 4 6 8
>> V2 = [l 2 3 4]
V2 =
1 2 3 4
>> V1 / V2
Ans =
>> V1.* V2
ans =
2 8 18 32
10.1. Арифметические операторы и функции
Арифметические операторы являются самыми распространёнными и известными. В отличие от большинства языков программирования, в системе MATLAB практически все операторы являются матричными, то есть, предназначены для выполнения операций над матрицами. В табл. 1 приводится список арифметических операторов и синтаксис их применения.
Таблица 1
| Функция | Название | Оператор | Синтаксис |
| plus | Плюс | + | M1 + M2 |
| unplus | Унарный плюс | + | + M |
| minus | Минус | -- | M1 - M2 |
| unminus | Унарный минус | - | - M2 |
| mtimes | Матричное умножение | * | M1 * M2 |
| times | Почленное умножение массивов | .* | A1.* A2 |
| mpower | Возведение матрицы в степень | ^ | M1 ^ x |
| power | Почленное возведение матрицы в степень | .^ | A1. ^x |
| mldivide | Обратное (справа налево) деление матриц | \ | M1 \ M2 |
| mrdivide | Деление матриц слева направо | / | M1 / M2 |
| idivide | Почленное деление массивов справа налево | .\ | A1. \ A2 |
| rdivide | Почленное деление массивов слева направо | ./ | A1. / A2 |
| kron | Тензорное умножение Кронекера | kron | kron (X, Y) |
10.2. Элементарные встроенные функции
В тригонометрических функциях углы измеряются в радианах. Все функции могут использоваться в конструкции вида y = func(x), где func – имя функции. Обычно в такой форме задаётся информация о функции в системе MATLAB. Мы, однако, будем использовать для функций, возвращающих одиночный результат, более простую форму func(x). Форма [y,z,...] = func(x,...) будет использоваться только в тех случаях, когда функция возвращает множественный результат.
10.3. Алгебраические и арифметические встроенные функции
Ø abs (X) возвращает абсолютную величину для каждого числового элемента вектора X. Если X содержит комплексные числа, abs (X) вычисляет модуль каждого числа. Примеры:
>> abs (-5)
ans =
>> abs ([l - 2i 3i 2 + 3i)
ans =
2.2361 3.0000 3.6056
|
|
|
Ø ехр (Х) возвращает экспоненту для каждого элемента X.
>> ехр ([1 2 3])
ans =
2.7183 7.3891 20.0855
Ø factor (n) возвращает вектор-строку, содержащую простые множители числа n. Для массивов эта функция неприменима. Пример:
>> f = factor (5)
f =
Ø sqrt (x)- вычисление квадратного корня из элементов массива х. Для отрицательных и комплексных элементов x функция принимает комплексные значения.
> sqrt (25)
ans =
>> sqrt (-25)
ans =
0 + 5.0000i
Вычисление логарифмов
1) log (x) - натуральный логарифм,
2) log2 (x) -возвращает логарифм по основанию 2 элементов массива х.
3) log10 (x) - по основанию 10
Примеры:
>> x = [1. 2 3. 34 5 2. 3]
x =
1. 2000 3. 3400 5. 0000 2. 3000
>> log (x)
ans =
0. 1823 1. 2060 1. 6094 0. 8329
>> log 10 (x)
ans =
0. 0792 0. 5237 0. 6990 0. 3617
>> log 2 (x)
ans =
0. 2630 1. 7398 2. 3219 1.2016
10.4. Тригонометрические и обратные встроенные функции
Для тригонометрических функций sin (x), asin (x), cos (x), acos (x), tan (x), atan (x), cot (x) возвращается значение функции для каждого элемента Х (если задан вектор).
Примеры:
>> x = [1 3 5 2.3]
x =
1. 0000 3. 0000 5. 0000 2. 3000
>> cos (x)
ans =
0. 5403 -0. 9900 0. 2837 -0. 6663
10.5. Примеры записи математических выражений
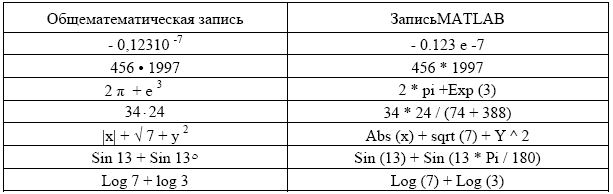
При записи на языке программирования любое математическое выражение должно быть " вытянуто в одну строчку ", а приоритет операций регулируют скобки. Рассмотрим в табл. 2 несколько примеров записи выражений.
Таблица 2
11. Функции комплексного аргумента
Числа могут быть комплексными: Z = a + b * i. Такие числа содержат действительную Re(z) и мнимую Im(z) части. Мнимая часть имеет множитель i или j, означающей корень квадратный
из -1:
3 i
2 j
2 + 3 i
-3. 14 i
-123. 456 + 2.7 e -3i
Ниже даны простейшие примеры работы с комплексными числами:
>> i
ans =
0 + 1. 0000i
>> z = 2 + 3i
z =
2. 0000 + 3. 0000 i
>> abs (z)
ans =
3. 6056
>> real (z)
ans =
>> imag (z)
ans =
>> angle (z)
ans =
0. 9828
Для работы с комплексными числами и данными в MATLAB используются следующие встроенные функции.
Ø imag (Z) возвращает мнимые части всех элементов массива Z. Пример:
» Z = [l + i, 3 + 2i, 2 + 3i];
» imag (Z)
ans =
1 2 3
Ø real (Z) возвращает вещественные части всех элементов комплексного массива Z. Пример:
» Z = [l + i, 3 + 2i, 2 + 3i];
» real (Z)
ans =
1 3 2
Ø conj (Z) возвращает число, комплексно-сопряжённое аргументу Z. Если Z комплексное, то conj (Z) = real (Z) - i * imag (Z);
» conj (2 + 3i)
ans =
2.0000 - 3.0000i
Ø abs(z) служит для получения модуля комплексного числа;
» Z = 3 + i * 2
Z =
3.0000 + 2.0000i
» R = abs (Z)
R =
3. 6056
Ø angle (Z) служит для получения аргумента комплексного числа, углы лежат в диапазоне
[- π; + π], в радианах;
» theta = angle (Z)
theta =
0. 5880
– Формула Z = R.* exp (i * theta) даёт переход от показательной формы представления комплексного числа к алгебраической;
» Z = R.* exp (i * theta)
Z =
3. 0000 + 2. 0000 i
11.1. Системы линейных уравнений с комплексными коэффициентами
|
|
|
Программа MATLAB позволяет легко решать системы линейных уравнений с комплексными коэффициентами. Предположим, что дана система линейных уравнений:

Требуется найти токи I1 и I2. Для решения системы используется матрица коэффициентов R и матрица свободных членов F. Решение находится в виде произведения обратной матрицы коэффициентов на матрицу свободных членов:
F R W ⋅ − = 1
Ниже (рис. 9) приведён фрагмент программы MATLAB, который показывает порядок решения системы линейных уравнений с комплексными коэффициентами.
Таким образом, ток I1 = – 0. 0041 – 0. 0150i, а ток I2 = – 0. 0196 – 0. 0233i.

Рис. 9. Фрагмент программы MATLAB
12. Погрешность измерения величин
Пусть x – приближённое значение некоторой величины (например, полученное путём однократного измерения этой величины), а x 0 – её точное значение
Абсолютной погрешностью величины называется разность Δx = |x – x0|.
Пример. В школе 1254 учащихся. При округлении этого числа до 1200 абсолютная погрешность составляет Δ = |1200 – 1254| = 54, а при округлении до 1250: Δ = |1250 – 1254| = 4.
Относительной погрешностью приближённого числа называется отношение абсолютной погрешности приближённого числа к самому этому числу:

Пример
В школе 1254 учащихся. При округлении этого числа до 1200 абсолютная погрешность составляет
Δ = |1200 – 1254| = 54, относительная погрешность равна  или 4,3 %.
или 4,3 %.
При округлении до 1250: Δ = |1250 – 1254| = 4, а относительная погрешность  или 0,3 %.
или 0,3 %.
В научных экспериментах многие величины определяются не непосредственно, а косвенным путём – измерением значений других величин. Так, чтобы найти плотность тела, измеряют его массу, взвешивая на весах, после чего определяют объём тела, погружая его в жидкость. Плотность выражается через массу и объём тела.
ρ=m/V
Масса и объём, входящие в эту формулу, измеряются с некоторой погрешностью; это означает, что и плотность, вычисленная по этой формуле будет иметь погрешность.
Существуют несколько правил, позволяющих рассчитывать погрешности величин.
Абсолютная погрешность суммы двух независимых величин равна сумме абсолютных погрешностей отдельных слагаемых: Δ(x + y) = Δx + Δy.
Абсолютная погрешность разности двух независимых величин равна сумме абсолютных погрешностей уменьшаемого и вычитаемого: Δ(x – y) = Δx + Δy.
Относительные погрешности при сложении и вычитании складывать нельзя.
Относительная погрешность произведения приближённо равна сумме относительных погрешностей отдельных сомножителей: ε(xy)≈ε(x)+ε(y), в частности ε(x/y)≈ε(x)+ε(y)
Пример 12.1.
Определить, какое равенство точнее: 911 = 0,818; 18 = 4,24;.
Решение.
Найдём значения данных выражений с большим числом десятичных знаков. Для этого выполним следующие действия:
>> format long % длинное представление числа (15 знаков)
>> a1=9/11
a1 =
0.81818181818182
>> a2=sqrt(18)
a2 =
4.24264068711928
Затем вычислим предельные абсолютные погрешности:
>> abs(a1-0.818)
ans =
E-004
>> abs(a2-4.24)
ans =
0.00264068711928
Округлим их с избытком:
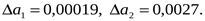
Вычислим предельные относительные погрешности:
>> 0.00019/0.818
ans =
E-004
>> 0.0027/4.24
ans =
E-004
Таким образом,


Так как  , то равенство 9/11 = 0,818 является более точным.
, то равенство 9/11 = 0,818 является более точным.
Пример 12.2.
Округлить сомнительные цифры числа a, оставив верные знаки:
Решение.
Пусть а = 2,3544; δа = 0,2%; тогда Δа = а· δа = 0,00471. В данном числе верными являются три цифры, поэтому округляем его, сохраняя эти цифры:
а = 2,3544; Δа1 = Δа+ Δокр= 0,0044+0,00471=0,00911<0,01
Значит, и в округлённом числе 2,35 все три цифры верны.
Пример 12.3.
Найти предельную абсолютную и относительную погрешности числа 12,384, если оно имеет только верные цифры.
Решение.
Так как все пять цифр числа а=12,384 верны, то 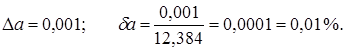
Пример 12.4.
Вычислить и определить погрешности результата  ,
,
где n = 3,0567(±0,0001), m = 5,72(±0,02).
Решение.
Имеем:

Ответ: 
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие окна имеет интерфейс MATLAB, их назначение?
2. Какова структура окна Command Windows?
3. Как очистить окно Command Windows?
4. Как в MATLAB осуществляется ввод и выполнение команд?
5. Как увеличить длину командной строки Command Windows, распространив её на несколько физических строк командного окна?
6. Что называется рабочей областью MATLAB?
7. Как осуществляется просмотр и редактирование значений переменных в окне Workspace?
8. Как отобразить список переменных, созданных в данном сеансе работы, в командном окне?
9. Как удалить неиспользуемую более переменную из рабочего пространства MATLAB?
10. Как получить справку по выбранной команде MATLAB?
11. Для чего служит редактор М-файлов?
12. Как вызвать редактор М-файлов, и какие отладочные средства он имеет?
13. Как осуществляется цветовые выделения и синтаксический контроль при работе с пакетом MATLAB?
14. Как можно получить быструю справку по любой команде MATLAB?
15. Расскажите о MATLAB в роли супер калькулятора.
16. Что принято называть сессией при работе с MATLAB?
17. Как изображается и для чего служит комментарий?
18. Что такое интерактивный режим?
19. Перечислите основные объекты, с которыми работает MATLAB.
20. В каком окне можно скорректировать данные, занесённые в рабочую область и как вызвать это окно?
21. Что такое системные переменные MATLAB их идентификаторы?
22. Перечислите системные переменные и назовите, какие значения принимает каждая системная переменная по умолчанию.
23. Перечислите типы переменных, используемых в MATLAB.
24. Правила задания имени переменной.
25. Как присвоить переменной значение?
26. В каком формате в MATLAB представляются вещественные числа?
27. Какие форматы отображения вещественных чисел используются в MATLAB?
28. Как в MATLAB осуществляются операции с комплексными числами?
29. Как в MATLAB осуществляются операции с матрицами?
30. Перечислите основные арифметические операторы и их синтаксис
31. в системе MATLAB
32. Что такое встроенная функция? Перечислите алгебраические и арифметические встроенные функции в MATLAB.
33. Перечислите тригонометрические и обратные встроенные функции в MATLAB.
34. Записать выражение в MATLAB: 2π + а 4.
35. Записать выражение в MATLAB: Sin 45 + Sin 45°.
36. Чем отличается действительное число от комплексного числа? Правила записи комплексных чисел в системе MATLAB.
37. Перечислите функции комплексной переменной в системе MATLAB.
38. Алгоритм решения системы линейных уравнений с комплексными коэффициентами.
ПРАКТИЧЕСКИЕ ЗАДАНИЯ
ЗАДАНИЕ 1:
а) вычислить значение функции y = f(x) в точке х0
б) простроить график функции y = f(x) используя встроенную функцию MatLab poly(x,y) на интервале от х0 до хn , шаг аргумента x определить самостоятельно
Варианты заданий.
| № варианта | Функция | х0 | хn |

| 5,5 | 8,5 | |

| 2,75 | 4,2 | |

| 3,1 | 4,0 | |

| 4,21 | 7,6 | |

| 6,32 | 7,8 | |

| 4,75 | 6,25 | |

| 2,35 | 4,55 | |

| 8,29 | 12,49 | |
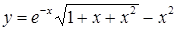
| 4,56 | 6,25 | |

| 1,23 | 12,0 | |
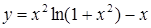
| 7,55 | 9,65 |
Пример выполнения задания:
>> x=4.75;
>> y=(2/3*(sin(2*x))^2)-(3/4*(cos(2*x))^2)
y =
-0.7420
>> x=4.75:0.05:5; % задание вектора аргумента (x0:шаг аргумента:xn)
>> y=(2/3*(sin(2*x)).^2)-(3/4*(cos(2*x)).^2)
y =
-0.7420 -0.7069 -0.6454 -0.5597 -0.4534 -0.3307
>> plot(x,y)

Рис. 10. График функции 
со списком элементарных функций MatLab можно ознакомиться, набрав команду
>> help elfun
со списком операторов
>> help ops
Чтобы очистить командное окно, необходимо из меню Clear Command выбрать команду Command Window, очистить историю команд, Command History (Рис. 11)
Рис. 11. Использование команд меню Clear Command.
ЗАДАНИЕ 2.
1. Определить, какое равенство точнее.
2. Округлить сомнительные цифры числа, оставив верные знаки.
3. Найти предельную абсолютную и относительную погрешности числа, если они имеют только верные цифры.
4. Вычислить и определить погрешности результата.
Варианты заданий.
| № варианта | Задание |

| |
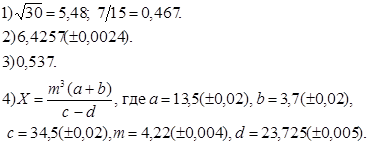
| |

| |

| |

| |

| |

| |

| |

| |

| |
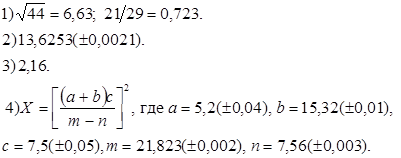
| |
|
|
|
12 |


