 |
Часть I. Теория стоимости денег во времени
|
|
|
|
ФГБОУ ВПО ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПО ЗЕМЛЕУСТРОЙСТВУ
Факультет земельного кадастра Кафедра землепользования и кадастров
ОЦЕНКА ЗЕМЛИ И ИНОЙ НЕДВИЖИМОСТИ
Методические указания
По выполнению расчетно-графической работы
Факультет – «Земельный кадастр» Специальность – 120302 «Земельный кадастр»
Москва 2012
УДК 330.322.12 332.365 631.162
Подготовлены и рекомендованы к печати кафедрой землепользования и кадастров Государственного университета по землеустройству (протокол № 02 от 13.09.2010 г.).
Утверждены к изданию методической комиссией факультета земельный кадастр Государственного университет по землеустройству (протокол № от.0.2010 г).
Составил: доцент к.э.н. С.И. Комаров
Рецензенты: - доцент, к.э.н. член российского общества оценщиков И.В. Подкова
- старший преподаватель, к.э.н. Д.В. Антропов
© ГУЗ, 2012
Содержание
Введение.................................................................................................................................. 3
Часть I. Теория стоимости денег во времени...................................................................... 3
Часть II. Оценка объекта недвижимости доходным подходом......................................... 3
Часть III. Оценка объекта недвижимости сравнительным подходом.............................. 3
Часть IV. Оценка объекта недвижимости затратным подходом....................................... 3
Часть V. Согласование результатов оценки........................................................................ 3
Заключение.............................................................................................................................. 3
Рекомендуемая литература.................................................................................................... 3
Примеры тестовых вопросов................................................................................................ 3
|
|
|
Приложение. Варианты исходных данных для выполнения расчетно-графической работы 3
Введение
Становление капитализма в России, более глубокое внедрение страны в глобальную мировую экономику, упорядочение отношений собственности приводят к тому, что на первые роли выходят сферы деятельности, которые ранее либо не существовали вовсе, либо не имели столь важного влияния на экономику. Значение адекватной, отвечающей текущему состоянию рынка оценки активов предприятия или его самого целиком приобретает высокую значимость. Тем актуальнее становятся работы, раскрывающие применение различных теоретических и методических аспектов оценки стоимости предприятия (бизнеса).
Результатом реформ 90-ых годов стало появление в России частных собственников на помещения, здания и сооружения сначала жилищного, а затем общественного и промышленного назначения. Постепенно капиталистические отношения проникали и в сферу земельных ресурсов. Таким образом, постепенно Россия становиться в один ряд с развитыми капиталистическими странами, где недвижимость составляет основу национального богатства и лежит в самой основе частных имущественных прав. Интересы собственников по сравнению с лицами, не являющимися таковыми, более защищены, и они постоянно работают над увеличением стоимости своей собственности.
В настоящее время во всем мире недвижимость наряду с человеческими, финансовыми, материально-техническими и информационными является одним из необходимых видов ресурсов для эффективной деятельности любого бизнеса. При этом недвижимость является важнейшим имущественным компонентом собственников. По своей оценочной стоимости недвижимость составляет до 30 – 40% основных фондов производственных предприятий, а в некоторых отраслях и видах деятельности — до 70 – 80%. Поэтому многие современные экономисты и политологи считают, что широкое распространение частной собственности на недвижимость является жизненно важным для поддержания демократии и устойчивости политического строя.
|
|
|
Развитие и становление рынка недвижимости в России в целом и в отдельных регионах в частности, а также осуществление некоторых национальных проектов приводит к высокой актуальности всех вопросов, связанных со строительством, оборотом недвижимости и девелопментом. Сегодня недвижимость не только на западе, но и в России стала одним из популярных способов инвестирования капитала. Все эти обстоятельства делают актуальными работы, связанные с проведением оценки отдельных активов или целых предприятий, работающих в данной сфере.
В начале ХХI века Россия является одним из самых динамично развивающихся и привлекательных для различных групп инвесторов рынков недвижимости в мире. При этом, по
оценкам самых различных экспертов, потенциал, заложенный в
отечественном рынке недвижимости, очень велик. Такое мнение основано на том факте, что пока развиваются рынки недвижимости только в крупных городах. Рынок земли и участие ее в инвестиционных процессах, несмотря на существенный отрезок времени, прошедший с момента принятия Земельного кодекса РФ, легализировавшего куплю-продажу земли, во многих регионах не развит или развит крайне слабо.
Кроме того, проводимая в России пенсионная реформа, способствующая появлению в стране крупных институциональных инвесторов, действия федерального
правительства и руководства отдельных субъектов,
направленные на привлечение в сферу недвижимости банковского капитала, общая экономическая и политическая стабилизация и экономический рост, способствующий приходу на российский рынок крупных международных инвестиционных компаний, вместе с высокой доходностью рынка дают основания полагать, что в ближайшие годы отечественная недвижимость станет одним из самых привлекательных активов для российских и иностранных инвесторов.
Улучшение инвестиционного климата, рост количества инвесторов и объемов инвестиций привело к актуальности теории оценки земли и иной недвижимости. Задача эта усложняется и тем, что с одной стороны отечественная школа оценки имеет глубокие корни, с другой теория и практика
|
|
|
рыночной оценки на протяжении всего советского периода была не востребована и не развивалась.
Задачи анализа в процессе оценки недвижимости сводятся к исследованию процессов ценообразования конкретных объектов, как под влиянием его конкретных физических свойств, так и с
помощью рыночных механизмов, а также всякого рода других
случайных и систематических воздействий.
Задача синтеза заключается в вычислении критерия, объективно отражающего все вышеозначенные взаимодействия, таковым критерием и является стоимость объекта
недвижимости.
Учебным планом факультета «Земельный кадастр» предусмотрено на 4-ом курсе выполнение расчетно-графической работы по дисциплине «Оценка земли и иной недвижимости». Работа состоит из пяти частей и в процессе ее выполнения студент должен продемонстрировать знания и навыки по оценке конкретного объекта недвижимости, приобретенные на лекционных и семинарских занятиях.
В первой части работы студент демонстрирует знания теории сложного процента на примере решения группы задач по вариантам.
Во 2 – 4 частях необходимо найти рыночную стоимость объекта недвижимости доходным, сравнительным и затратным подходом соответственно.
В заключительной части подводятся итоги проделанной
работы, производится согласование результатов оценки и определение итоговой стоимости объекта.
Часть I. Теория стоимости денег во времени
В процессе проведения оценки любого объекта недвижимости оценщику приходится постоянно учитывать денежные потоки, относимые к разным промежуткам времени. Это может быть поток, генерируемый год от года оцениваемым объектом при использовании метода дисконтированных денежных потоков, или стоимость объекта-аналога, проданного некоторое время назад, или затраты на строительство, данные в ценах предыдущих лет.
Сравнивать эти потоки, а также производить с ними арифметические действия без предварительной подготовки некорректно, т.к. покупательная способность одной и той же денежной суммы в различные временные периоды разная.
|
|
|
Различная стоимость денежной единицы обуславливается следующими причинами:
• влиянием инфляции, снижающей покупательную способность денежных средств;
• колебаниями на рынках товаров и услуг (на различных
сегментах рынка недвижимости);
• потерей части дохода из-за получения денежные средств не сейчас, а через определенный промежуток времени, и которая могла быть получена за этот промежуток при инвестировании этой суммы.
Таким образом, для сравнения или произведения арифметических действий все разновременные денежные потоки необходимо приводить к одному и тому же моменту времени. К какому именно моменту времени теоретически совершенно неважно, но так как все расчеты и отчет об оценке недвижимости составляется на определенную дату, то, как правило, все потоки приводятся именно к дате оценки.
Для данного приведения используется алгоритм, в финансовой математике носящий название шесть функций сложного процента или функций денежной единицы.
Как известно, проценты бывают простые и сложные. При простом исчислении по окончании каждого соответствующего периода процент начисляется исключительно на изначальную
сумму. При сложном исчислении процент за каждый
последующий период начисляется на основную сумму и на процентные выплаты за предыдущие периоды.
Функции сложного процента подразделяются на:
• будущую стоимость денежной единицы;
• будущую стоимость аннуитета;
• фактор фонда возмещения;
• текущую стоимость денежной единицы;
• взнос на амортизацию денежной единицы;
• текущую стоимость аннуитета.
Три первых функции применяются для пересчета текущих денежных сумм в будущие, а три последние – для пересчета будущих денежных единиц в текущие. Первый процесс называется компаундированием, а второй дисконтированием. Но на практике термин «компаундирование» не прижился и не используется, термин же «дисконтирование» применяется достаточно широко.
Рассмотрим случай, когда некоторая денежная сумма (обозначим ее PV) помещается на депозитный банковский счет под ежегодный процент i на n лет. Через год на счету окажется
следующая сумма:
.
На второй год банковский процент будет начисляться уже не только на сумму PV, но и на проценты за первый год, что можно записать следующим образом:
.
На третий год ситуация будет аналогичной с той лишь разницей, что процентная составляющая увеличиться:
.
Таким образом, в общем виде на какой угодно период накопленную сумму можно рассчитать по формуле:
|
|
|
, (1)
где: PV – текущая стоимость денежной единицы; FV – будущая стоимость денежной единицы;
i – процентная ставка;
n – количество временных периодов.
Необходимо обратить внимание, что показатели количества периодов и процентная ставка должны быть сопоставимыми. Так,
если проценты начисляются ежегодно, то n должно обозначать число лет, а i – годовую ставку, если же известно, что проценты начисляются ежемесячно, тогда формула (1) примет вид:
(2)
Приведенная формула называется функцией будущей стоимостью денежной единицы и используется для пересчета денежных потоков, отнесенных к настоящему, в их будущую стоимость.
Из приведенной формулы (1) не составляет труда вывести выражение, позволяющее найти текущую стоимость денежных потоков, отнесенных к будущим временным периодам:
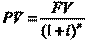. (3)
Эта функция носит название текущей стоимости денежной единицы.
Остальные четыре функции связаны с понятием аннуитетного платежа или аннуитета. Аннуитетом принято
называть равные денежные выплаты через равные промежутки
времени. Самым простым и наиболее распространенным примером аннуитетных выплат является арендная плата, поступающая на счет владельца недвижимости каждый месяц (квартал, год) от арендатора.
Если владелец недвижимого имущества захочет узнать, какая сумма накопиться у него на счету за срок арендного договора, то для расчетов ему будет необходимо воспользоваться функцией будущая стоимость аннуитета или накопление единицы за период:
, (4)
где: PMT – величина единичного аннуитетного платежа.
Обратная к будущей стоимости аннуитет функция носит название фактор фонда возмещения. Она применяется в случаях, если необходимо вычислить величину аннуитетного платежа, необходимого для накопления заранее известной суммы через определенный временной промежуток:
. (5)
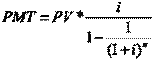В области оценки недвижимости часто приходится иметь дело с заемными средствами, кредитами на покупку или строительство объектов. Погашение полученного кредита в финансовой математике принято называть его амортизацией, именно поэтому функцию, применяемую для расчетов аннуитетных погашающих выплат при кредитовании, называют взнос на амортизацию единицы:
где PV – сумма кредита.
, (6)
Функция текущая стоимость аннуитета применяется при известных аннуитетных платежах, если необходимо определить, сколько сумма всех этих выплат представляет в текущем выражении. Данная функция является обратной к взносу на амортизацию единицы, поэтому принимает следующий вид:
. (7)
Все представленные функции сложного процента в совокупности представляют собой формализованное представление теории стоимости денег во времени. В теории и практике оценки недвижимости часты случаи применения данных функций, как будет видно в дальнейшем, практически ни один из методов оценки не обходится без применения указанных функций.
В практической деятельности кроме проведения расчетов, аналогичных приведенным выше примерам, широко используют
готовые таблицы функций сложного процента.
Например, если необходимо рассчитать сумму, которая можно скопить за искомый период следующим образом:
1. определить сумму ежегодного аннуитета,
2. найти фактор будущей стоимости аннуитета. Для этого открыть таблицу шести функций сложного процента для заданной ставки и на пересечении строки с номером года, соответствующем заданному сроку, и столбца с названием
«Будущая стоимость аннуитета» найти нужную величину;
3. перемножить величины аннуитетной выплаты и фактора будущей стоимости аннуитета.
Аналогичным образом можно применять таблицы шести функций сложного процента для расчетов с применением данных функций.
Рассмотрим применение шести функций сложного процента
на примере.
Владелец склада Петр Сидоров хочет скопить на ремонт склада, планируемый через три года. В настоящее время аналогичный ремонт стоит 500 тысяч рублей. Часть
стоимости ремонта Петр планирует скопить, откладывая из
ежегодного дохода по 75 тысяч рублей и внося эти деньги в банк под 8% годовых. А на остальную сумму взять кредит.
Для начала Сидоров решил узнать, сколько будет стоить ремонт через три года. Для этого он проанализировал рынок строительно-ремонтных работ и увидел, что в среднем данные
работы дорожают на 7% ежегодно, тогда применяя функцию
«Будущая стоимость единицы» можно узнать стоимость ремонта к моменту возникновения необходимости в нем:
рублей. Чтобы рассчитать сумму, которую он сможет скопить,
Петр решил посчитать будущую стоимость трехлетнего аннуитета:
.
По окончании требуемого срока он будет иметь в своем распоряжении 243 тысячи 750 рублей для ремонта. Таким образом, для осуществления ремонта Петру будет не хватать 368 тысячи 772 рубля. На эту сумму, как уже было сказано, Сидоров рассчитывает взять кредит. Средние банковские условия по кредитам таковы: 12% годовых с ежемесячными выплатами на 8 лет. Сколько же необходимо будет выплачивать владельцу склада по кредиту? Для ответа на этот вопрос наиболее целесообразно применить функцию «Взнос на амортизацию единицы»:
рублей, т.е. для погашения кредита Сидорову будет необходимо
выплачивать 5 тысяч 992 рубля 8 копеек ежемесячно.
Для выполнения первой части расчетно-графической работы студенту необходимо решить задачи с использованием функций сложного согласно своему варианту. Исходные данные для выполнения первой части РГР приведены ниже.
Вариант 1
1. Владелец гостиницы планирует сделать ремонт через 5 лет. В настоящее время стоимость ремонта составляет 100 тысяч и дорожает на N% в год. Какую сумму ежемесячно должен класть
владелец в банк под 10% годовых, чтобы в итоге скопить
требуемую сумму?
2. За какой срок денежная сумма, положенная в банк под N%
годовых, удвоится?
3. Семья планирует взять кредит и выплачивать за него не более 3500 рублей ежемесячно. Средние банковские условия таковы: срок кредита 8 лет под 12% годовых. Какую долю от квартиры стоимостью 1 млн рублей сумеет профинансировать семья?
4. В настоящий момент Андрей Иванов имеет 50 000 рублей свободных средств для осуществления личных инвестиций на срок пять лет. В процессе анализа возможных объектов вложений он обратил внимание на инвестиционный фонд А, обещающий своим вкладчикам 15% годовых с ежеквартальным начислением дохода на счета клиентов. Сколько составят сбережения Андрея через 5 лет?
Вариант 2
1. Владелец гостиницы планирует сделать ремонт через 3 года. В настоящее время стоимость ремонта составляет 150 тысяч и дорожает на N% в год. Какую сумму ежемесячно должен класть
владелец в банк под 10% годовых, чтобы в итоге скопить
требуемую сумму?
2. Под какой процент следует положить денежную сумму в банк, чтобы через N лет она утроилась?
3. Семья планирует за N лет скопить на обучение ребенка, которое сейчас стоит 3 000 000 рублей и дорожает на 8% в год. При этом за эти годы семья планирует 40% от требуемой суммы
скопить, ежеквартально кладя деньги в банк под 12% годовых, а
потом на оставшуюся часть взять кредит на следующие 5 лет под 15% годовых с ежемесячными выплатами. Сравните денежные суммы, которые семья должна класть на счет в первые годы, и которые должна выплачивать банку в последующем.
4. Сколько будет через три года стоить склад, способный приносить ежемесячно N тысяч рублей чистого дохода? Известно, что ежегодно складская недвижимость дорожает на 10%, а средняя банковская ставка по вкладам – 8% годовых.
Вариант 3
1. Господин Петров за 20 млн рублей приобрел склад, сданный в аренду на 10 ближайших лет с ежеквартальной выплатой арендной платы. Хватит ли ему получаемого дохода для выплаты ипотечного кредита, выданного на N лет под 12 процентов годовых? Выплаты по кредиту осуществляются ежемесячно, а среднегодовая инфляция – 10% годовых.
2. Какую сумму нужно вложить в банк сейчас под 9% годовых, чтобы получить через 10 лет N млн рублей?
3. Семья планирует за 7 лет скопить на обучение ребенка, которое сейчас стоит 450 000 рублей и дорожает на N% в год.
При этом за эти годы семья планирует 35% от требуемой суммы
скопить, ежеквартально кладя деньги в банк под 11% годовых, а потом на оставшуюся часть взять кредит с ежемесячными выплатами на следующие 5 лет под 14% годовых. Сколько семья должна класть на счет в первые годы и выплачивать банку в последующие.
4. Владелец небольшого бизнеса Иван Конев с ежемесячным доходом 4*N тысяч рублей планирует взять кредит на покупку квартиры стоимостью 1,5 млн рублей. Средние банковские условия состоят в сумме, не превышающей 70% от стоимости объекта на 15 лет под 15% годовых с ежемесячными равными
выплатами в течение всего срока. Какую же сумму ему придется платить каждый месяц для выплаты кредита?
Вариант 4
1. ООО «Лютик» планирует приобрести офисное здание, сданное в аренду на 10 лет за 20 млн рублей в год. Сколько необходимо будет выплачивать компании ежеквартально банку для погашения кредита на покупку, выданного на N лет под 12% годовых?
2. На какую сумму кредита, выдаваемого на 10 лет под 15% годовых, может рассчитывать заемщик, если он хочет выплачивать не больше 15 000 рублей в месяц?
3. Семья планирует взять кредит и выплачивать за него не более N тысяч рублей ежемесячно. Средние банковские условия таковы: срок кредита N лет под 11% годовых. Какую долю от покупку квартиры стоимостью 1,5 млн рублей сумеет профинансировать семья с помощью кредита?
4. Молодая семья хочет скопить за десять лет 500 тысяч рублей на образование своего ребенка. Одним из вариантов является помещение имеющихся 80 тысяч рублей на банковский депозит под N% годовых с ежеквартальным начислением процентов. Сколько необходимо поместить на банковский счет, чтобы скопить требуемую сумму?
Вариант 5
1. Господин Зеленов приобрел место на парковке за 180 000 рублей. Он рассчитывает сдавать его в аренду за 20 000 ежегодно, с ежегодными выплатами в течение ближайших 8 лет. В конце этого срока он хочет продать это место за 200 000. Получит ли Зеленов 15%-ную отдачу от своих вложений при ставке дисконта N%?
2. Какова текущая стоимость ипотечного кредита, предусматривающая ежемесячную выплату 20 000 рублей на протяжении N лет при ставке кредита в 10%?
3. В конце 12-го года инвестиции принесут 1,5 млн рублей. Владелец инвестиционного актива должен погасить через N года долг в 600 тысяч рублей. Сколько инвестору следует заплатить
за инвестиционный актив, если он рассчитывает получать на свое вложение 10%-ный доход?
4. Какова сумма окажется на счету через 7 лет, если ежеквартально вносить на счет 45 000 рублей под N% годовых?
|
|
|
