Приближённые значения чисел. Абсолютная и относительная погрешности.

Тема 1. Развитие понятия о числе

Аннотация: Учебное пособие разработано в соответствии с Рабочей программой общеобразовательной учебной дисциплины Математика: алгебра и начала математического анализа; геометрия.

Учебное пособие содержит:

ü теоретический материал;

ü практический материал для освоения основных, предусмотренных стандартом, умений и накопления опыта в использовании приобретенных знаний и умений в практической деятельности и повседневной жизни;

ü контрольные вопросы и задания.

 

 

Тема 1. Развитие понятия о числе

Действительные числа

Числовые множества

N – множество натуральных чисел	R – множество всех действительных чисел
Z– множество целых чисел
Q – множество рациональных чисел
I– множество иррациональных чисел

Рациональные числа

Обыкновенные дроби.

Обыкновенная дробь – это число вида , где m и n – натуральные числа. Число m называется числителем дроби, n – знаменателем.

Всякое натуральное число можно представить в виде обыкновенной дроби со знаменателем 1.

Дробь называется правильной, если её числитель меньше знаменателя, и неправильной, если её числитель больше знаменателя или равен ему.

Основное свойство дроби: если числитель и знаменатель данной дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной.

Десятичные дроби.

Десятичная дробь – это любая числовая дробь, знаменатель которой равен 10, 100, 1000 и вообще 10ⁿ.

В виде десятичной дроби можно представить любую обыкновенную дробь, знаменатель которой является делителем некоторой степени числа 10.

Десятичная запись — это форма записи десятичных дробей, где целая часть отделяется от дробной с помощью обычной точки или запятой. При этом сам разделитель (точка или запятая) называется десятичной точкой.

Бесконечная десятичная дробь – после запятой содержится бесконечно много десятичных знаков.

Теорема. Любую обыкновенную дробь можно представить в виде бесконечной десятичной дроби.

Последовательно повторяющаяся группа цифр (минимальная) после запятой в десятичной записи числа называется периодом, а бесконечная десятичная дробь, имеющая такой период в своей записи, называется периодической. Для краткости принято период записывать один раз, заключая его в круглые скобки:

0,2121…= 0, (21) – чистая периодическая дробь, так как период начинается сразу после запятой;

2,3454545…= 2,3(45); 2, 73 = 2,73000…= 2,73(0) – смешанные периодические дроби, так как между запятой и периодом есть другие десятичные знаки.

 

Стандартный вид положительного действительного числа.

Любое положительное число a можно представить в виде ∙ 10 ⁿ, где , а n – целое число.

Показатель n называют порядком числа.

Примеры.

а = 395 = 3,95∙10²;

а = 4,13 = 4,13∙10⁰;

а = 0,0023 = 2,3∙10^-3.

Приближённые значения чисел. Абсолютная и относительная погрешности.

При округлении десятичной дроби до какого-нибудь разряда все следующие за этим разрядом цифры заменяют нулями, а если они стоят после запятой, то их отбрасывают.

Если первая следующая за этим разрядом цифра больше или равна пяти, то последнюю оставшуюся цифру увеличивают на 1.

Если же первая следующая за этим разрядом цифра меньше 5, то последнюю оставшуюся цифру не изменяют.

Приближённые значения появляются не только при округлении чисел. Чаще они возникают при различных измерениях (длин, масс, температур и т.д.). При этом важно знать, с какой точностью выполнено измерение.

Пусть а – приближённое значение числа .

Абсолютной погрешностью приближенного значения числа называется модуль разности чисел и а, то есть .

Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближённого значения. Относительную погрешность обычно выражают в процентах, то есть

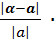100%

Пример. Взвесив кондитерское изделие, масса которого равна 54,12705 г, на весах с ценой деления шкалы 0,1 г, получили приближённое значение массы 54,1 г. Найти абсолютную и относительную погрешности этого приближённого значения.

Решение.

1) = (абсолютная погрешность);

 

2) 100% = 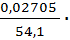100% = 0,05% (относительная погрешность).

 

Если абсолютная погрешность приближённого значения а, найденного для интересующего числа , не превосходит некоторого числа h, то пишут ; говорят, что а – приближённое значение числа с точностью до h.

 

12	Поделиться:

Воспользуйтесь поиском по сайту: