Задачи на растворы и концентрацию.

Концентрация раствора - это часть, которую составляет масса растворённого вещества от массы всего раствора.

Задача 1. Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора? (Масса 1 л воды составляет 1 кг)

Решение.

1 кг - масса растворённого вещества (соли);

9 кг - масса воды в растворе (не путать с общей массой раствора);

9 + 1 = 10 кг - общая масса раствора;

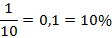
Ответ: 10%

 

Задача 2. Сколько соли получится при выпаривании 375 граммов 12%-го раствора?

Решение.

Чтобы найти массу выпаренной соли из раствора, умножим общую массу раствора на процент концентрации. Не забудем предварительно перевести процент в десятичную дробь.

1) 12% = 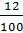= 0,12;

2) 375 · 0,12 = 45 (г).

Ответ: 45 граммов соли.

 

Задача 3. В сосуд, содержащий 5 литров 12–ти процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

Решение.

В решении подобных задач помогает картинка. Изобразим сосуд с раствором схематично — так, как будто вещество и вода в нем не перемешаны между собой, а отделены друг от друга, как в коктейле. И подпишем, сколько литров содержат сосуды и сколько в них процентов вещества. Концентрацию получившегося раствора обозначим х.

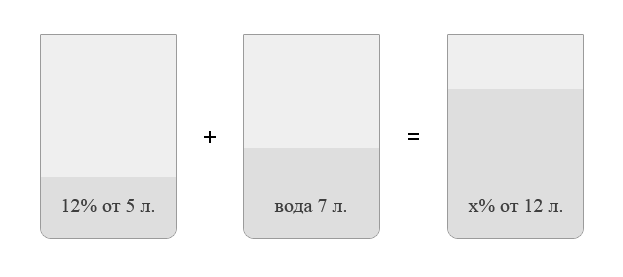
Первый сосуд содержал 0,12 · 5 = 0,6 литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом, составим уравнение: 0,12 · 5 = 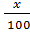·12; x = 5 (%).

Ответ: 5%.

 

Задача 4. Смешали некоторое количество 15-ти процентного раствора некоторого вещества с таким же количеством 19-ти процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение.

Пусть масса первого раствора равна х. Масса второго — тоже х. В результате получили раствор массой 2 х. Рисуем картинку.

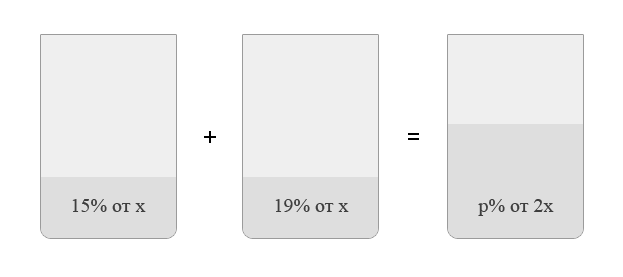
0,15 х + 0,19 х = 0,34 х = 0,17· 2 х

0,17 = 17%

Ответ: 17%

 

Задача 5. Виноград содержит 90% влаги, а изюм — 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма?

Решение.

Внимание! Если вам встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог — знайте, что на самом деле это задача на растворы. Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка. Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным. В винограде содержалось 90% воды, значит, «сухого вещества» было 10%. В изюме 5% воды и 95% «сухого вещества».

Пусть из х кг винограда получилось 20 кг изюма. Тогда 10% от х = 95% от 20.

Составим уравнение:

0,1 х = 0,95· 20; 0,1 х = 19; х = 190 (кг)

Ответ: 190 кг.

 

Задача 6. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

Решение.

Пусть масса первого раствора х, масса второго равна у. Масса получившегося раствора равна х + у + 10. Запишем два уравнения для количества кислоты.

Решаем получившуюся систему. Сразу умножим обе части уравнений на 100, поскольку с целыми коэффициентами удобнее работать, чем с дробными. Раскроем скобки и найдем корни уравнения:

 

 

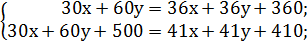
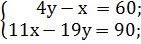
; у = 30.

Ответ: 60 кг.

 

ПРАКТИЧЕСКАЯ ЧАСТЬ

Выполните задания для подготовки к проверочной работе.

 

1. Запишите следующие числа в виде периодических десятичных дробей и округлите их с точностью до 0,001:

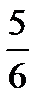а) ; б) ; в) .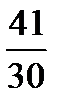

2. Представьте данные числа х в виде десятичных дробей с указанной точностью округления h.

а) х = 3,06527 h = 1; 0,1; 0,01; 0, 001; 0,0001

б) х = 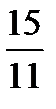h = 1; 0,1; 0,01; 0, 001

3. Запишите число в стандартном виде. Укажите его порядок и округлите его мантиссу до тысячных.

а) 60,396; б) 357 10⁶; в) 0,0004756.

4. Масса спутника Юпитера Каллисто равна 107660000000000000000 тонн. Запишите массу Каллисто (в тоннах) в стандартном виде.

5. Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25%?

6. Из 5 т хлопка получается 1,2 т волокна. Сколько тонн надо пе­реработать хлопка, чтобы получить 6 т волокна?

7. Токарь выточил за день 54 детали, что составило 75% его дневной нормы. Какова дневная норма токаря?

8. Найдите неизвестный член пропорции .

9. Мяч стоил 200 рублей. Эта сумма была снижена на 15%, а через некоторое время новая цена была снижена на 20%. Сколько стал стоить мяч после второго снижения?

10. В один стакан чая обычно кладут 3 чайные ложки сахара и считают такой чай сладким. Масса чая в стакане 200г, масса сахара в одной ложке 10г. Какова концентрация сахара в чае?

11. Какое количество воды нужно добавить в 500 мл 6% раствора уксуса, чтобы получить 3% раствор? Ответ запишите в литрах.

12. К 30% раствору серной кислоты добавили 40 г чистой кислоты, после чего концентрация раствора стала равной 50%. Найдите первоначальный вес раствора в граммах.

 

 

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ

1. Какие числа называются натуральными? Какое обозначение введено для множества натуральных чисел?

2. Какие числа входят в множество целых чисел? Какое обозначение принято для этого множества?

3. Какое множество называется множеством рациональных чисел и как это множество обозначается?

4. Перечислите основные законы действий над рациональными числами.

5. Какие обыкновенные дроби обращаются в конечные десятичные?

6. Какие обыкновенные дроби выражаются только приближенными десятичными?

7. Какие десятичные дроби называются бесконечными периодическими?

8. Что называется периодом бесконечной периодической десятичной дроби?

9. Какие периодические дроби называются чистыми и смешанными и как сокращенно они записываются?

10. Как записываются целые числа и конечные десятичные дроби в виде бесконечных периодических дробей?

11. Любая ли бесконечная периодическая десятичная дробь является рациональным числом?

12. Как обратить чистую периодическую десятичную дробь в обыкновенную?

13. Как обратить смешанную периодическую десятичную дробь в обыкновенную?

14. Какое исключение представляет собой бесконечная периодическая десятичная дробь с периодом 9?

15. Какие числа называются иррациональными и как обозначается множество иррациональных чисел?

16. Какие числа называются действительными и какое для них введено обозначение?

17. Что понимается под абсолютной величиной действительного числа?

18. Почему нельзя делить на нуль?

 

Дополнительное задание: написать реферат о возникновении и развитие чисел.

12	Поделиться:

Воспользуйтесь поиском по сайту: