 |
Случай прямоугольной области
|
|
|
|
Что значит вычислить двойной интеграл?
Двойные интегралы – это обобщение понятия определённого интеграла для функции двух переменных, заданной как z = f (x, y).
Записывается двойной интеграл так:
 .
.
Здесь D – плоская фигура, ограниченная линиями, выражения которых (равенства) даны в задании вычисления двойного интеграла. Слева и справа – равенствами, в которых слева переменная x, а сверху и снизу – равенствами, в которых слева переменная y. Это место и далее – одно из важнейших для понимания техники вычисления двойного интеграла.
Вычислить двойной интеграл - значит найти число, равное площади упомянутой фигуры D.
Пока мы не касаемся определения двойного интеграла, а будем учиться его вычислять. Понять, что такое двойной интеграл, проще, когда решены несколько задач на его вычисление, поэтому определение двойного интеграла вы найдёте в конце этого урока. Чуть забегая вперёд, можно лишь отметить, что определение двойного интеграла также связано с упоминавшейся фигурой D.
В случае если фигура D представляет собой прямоугольник, все линии, ограничивающие её – это прямые линии. Если фигура D - криволинейна, то слева и справа она ограничена прямыми, а сверху и снизу – кривыми линиями, заданными равенствами, которые даны в задании. Бывают и случаи, когда фигура D – треугольник, но о таких случаях чуть дальше.
Для вычисления двойного интеграла нужно, таким образом, рассортировать линии, огранивающие фигуру D, которая имеет строгое название – область интегрирования. Рассортировать на левые и правые и на верхние и нижние. Это потребуется при сведении двойного интеграла к повторному интегралу – методе вычисления двойного интеграла.
|
|
|
Случай прямоугольной области:
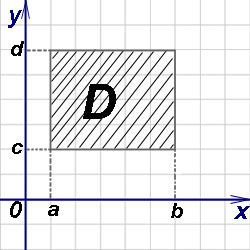
Случай криволинейной области:
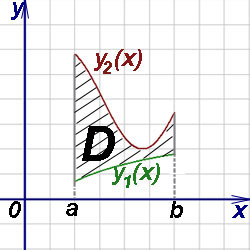
А это уже решение знакомых нам определённых интегралов, в которых заданы верхний и нижний пределы интегрирования. Выражения, задающие линии, которые ограничивают фигуру D, будут пределами интегрирования для обычных определённых интегралов, к которым мы уже подходим.
Сведение двойного интеграла к повторному
Случай прямоугольной области
Пусть дана функция двух переменных f (x, y) и ограничения для D: D = {(x; y) | a ≤ x ≤ b; c ≤ y ≤ d }, означающие, что фигуру D слева и справа ограничивают прямые x = a и x = b, а снизу и сверху - прямые y = c и y = d. Здесь a, b, c, d - числа.
Пусть для такой функции существует двойной интеграл
 .
.
Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид
 .
.
Здесь пределы интегрирования a, b, c, d - числа, о которых только что упоминалось.
Сначала нужно вычислять внутренний (правый) определённый интеграл, затем - внешний (левый) определённый интеграл.
Можно и поменять ролями x и y. Тогда повторный интеграл будет иметь вид
 .
.
Такой повторный интеграл нужно решать точно так же: сначала - внутренний (правый) интеграл, затем - внешний (левый).
Пример 1. Вычислить двойной интеграл
 ,
,
где
 .
.
Решение. Сводим данный двойной интеграл к повторному интегралу
 .
.
На чертеже строим область интегрирования:
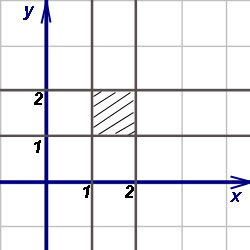
Вычисляем внутренний (правый) интеграл, считая игрек константой. Получаем.
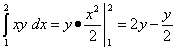 .
.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
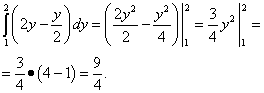
Результат и будет решением данного двойного интеграла.
Пример 2. Вычислить двойной интеграл
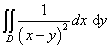 ,
,
где
 .
.
Решение. Сводим данный двойной интеграл к повторному интегралу
 .
.
На чертеже строим область интегрирования:
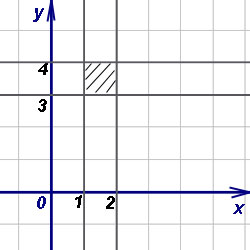
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.
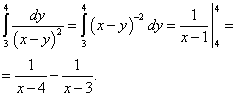
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
|
|
|
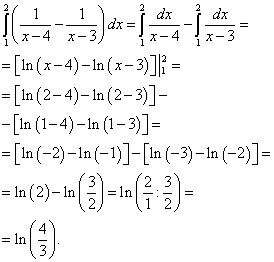
Результат и будет решением данного двойного интеграла.
|
|
|


