 |
Смена порядка интегрирования
|
|
|
|
Как уже отмечалось выше, после приведения двойного интеграла к повторному интегралу, можно поменять переменные x и y ролями, или, говоря иначе, поменять порядок интегрирования.
Смена порядка интегрирования образно может быть описана следующими словами О'Генри: "Так ведёт себя обитатель джунглей - зверь, попав в клетку, и так ведёт себя обитатель клетки - человек, заблудившись в джунглях сомнений". Результат, так же по О'Генри один и тот же: "Чалмерс разорвал письмо на тысячу мельчайших клочков и принялся терзать свой дорогой ковёр, расхаживая по нему взад и вперёд". (О'Генри. Шехерезада с Мэдисон-сквера.)
Тогда, если левый интеграл у нас по переменной x, а правый - по y, то после смены порядка интегрирования всё будет наоборот. Тогда пределы интегрирования для "нового" игрека нужно "позаимствовать" у "старого" икса, а пределы интегрирования для "нового" икса получить в виде обратной функции, разрешив относительно икса уравнение, задававшее предел для игрека.
Пример 6. Сменить порядок интегрирования для повторного интеграла
.
Решение. После смены порядка интегрирования интеграл по игреку станет левым, а интеграл по иксу - правым. Пределы интегрирования для "нового" игрека позаимствуем у "старого" икса, то есть нижний предел равен нулю, а верхний - единице. Пределы интегрирования для "старого" игрека заданы уравнениями 
и 
. Разрешив эти уравнения относительно икса, получим новые пределы интегрирования для икса:
(нижний) и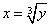 
(верхний).
Таким образом, после смены порядка интегрирования повторный интеграл запишется так:
.
После смены порядка интегрирования в двойном интеграле нередко область интегрирования превращается в y -неправильную или x -неправильную (см. предыдущий параграф). Тогда требуется разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно.
|
|
|
Поскольку разбиение области интегрирования на части представляет определённые трудности для многих студентов, то не ограничимся примером, приведённым в предыдущем параграфе, а разберём ещё пару примеров.
Пример 7. Сменить порядок интегрирования для повторного интеграла
.
Решение. Итак, область интегрирования данного повторного интеграла ограничена прямыми y = 1, y = 3, x = 0, x = 2 y.
При интегрировании в другом порядке нижняя граница области состоит из двух прямых: AB и BC, которые заданы уравнениями y = 1 и y = x /2, что видно на рисунке ниже.
Выход из такой неопределённости состоит в разбиении области интегрирования на две части. Делить область интегрирования будет прямая BМ. Новые пределы интегрирования вычисляем, находя обратную функцию. Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме двух интегралов:
Естественно, таким же будет решение двойного интеграла, который сводится к повторному интегралу, данному в условии этого примера.
Пример 8. Сменить порядок интегрирования для повторного интеграла
.
Решение. Итак, область интегрирования повторного интеграла ограничена прямыми x = 0, x = 2 и кривыми 
и 
.
Как видно на рисунке ниже, прямая, параллельная оси 0x, будет пересекать нижнюю границу области интегрирования более чем в двух точках.
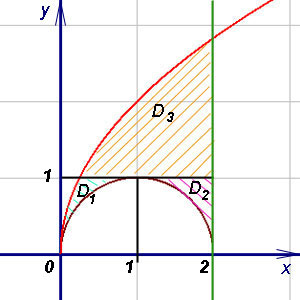
Поэтому разобьём область интегрирования на три части прямыми, которые на рисунке начерчены чёрным. Новые пределы интегрирования вычисляем, находя обратную функцию. Пределы для трёх новых областей интегрирования будут следующими.
Для 
:
Для 
:
Для 
:
Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме трёх интегралов:
|
|
|
Той же сумме трёх интегралов будет равен и двойной интеграл, который сводится к повторному интегралу, данному в условии этого примера.
И всё же обстоятельства непреодолимой силы нередко мешают студентам уже на предыдущем шаге - расстановке пределов интегрирования. Тревога и смятение не лишены некоторого основания: если для разбиения области интегрирования на части обычно достаточно приглядеться к чертежу, а для решения повторного интеграла - таблицы интегралов, то в расстановке пределов интегрирования нужен некоторый опыт тренировок. Пробежим пример, в котором остановимся только на расстановке пределов интегрирования и - почти на автомате - на разбиении области и опустим само решение.
Пример 9. Найти пределы интегрирования двойного интеграла, если область интегрирования D задана следующим образом:
y - 2 x ≤ 0;
2y - x ≥ 0;
xy ≤ 2.
Решение. В явном виде (через x и y "без примесей") линии, ограничивающие область интегрирования, не заданы. Так как для икса ими чаще всего оказываются прямые, касающиеся в одной точке верхней и нижней границ, выраженных через игрек, то пойдём именно по этому пути. Тем более, что при смене порядка интегирования мы получим область интегрирования с такой же площадью. Разрешим неравенства относительно игрека и получим:
y ≤ 2 x;
y ≥ x /2;
y ≤ 2/ x.
Строим полученные линии на чертёже. Пределами интегрирования по иксу действительно служат линии x = 0 и x = 2. Но область интегрирования оказалась y -неправильной, так как её верхнюю границу нельзя задать одной линией y = y (x).
Поэтому разобьём область интегрирования на две части при помощи прямой x = 1 (на чертеже - чёрного цвета).
Теперь данный двойной интеграл можем записать как сумму двух повторных интегралов с правильно расставленными пределами интегрирования:
.
|
|
|
