Краткие сведения из теории

Постановка задачи

В качестве объекта исследования выступают линейные (линеаризованные) динамические стационарные системы управления с одним входом и одним выходом. При этом модель одномерной САУ задана в виде комплексной передаточной функции, записанной как отношение полиномов

.

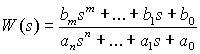Необходимо:

1. Определить полюса и нули передаточной функции

, .

2. Записать дифференциальное уравнение, определяющее функционирование САУ.

3. Построить графики переходной и импульсно-переходной функции:

h (t), w (t).

4. Построить логарифмические частотные характеристики

L (w).

5. Построить частотный годограф Найквиста

W (iw), w = [0, ¥ ].

6. Представить исходную систему в виде последовательного соединения типовых звеньев. Построить характеристики этих типовых звеньев.

Краткие сведения из теории

Рассмотрим систему автоматического управления (САУ), описываемую линейным (линеаризованным) дифференциальным уравнением вида:

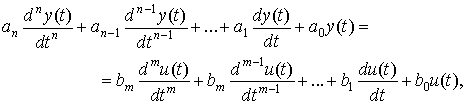(1.1)

где u (t) – входной процесс, y (t) – выходной процесс, a_i, b_j, () – постоянные коэффициенты, n, m (n ³ m) – постоянные числа. В операторной форме выражение (1.1) может быть записано –

.

Здесь D – оператор дифференцирования 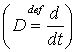. Отсюда преобразование “вход-выход” системы –

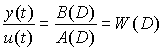, (1.2)

где W (D) называется операторной передаточной функции.

Один из способов моделирования систем заключается в представлении преобразования “вход-выход” в виде комплексной передаточной функции:

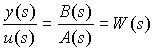, (1.3)

которая получается путем применения преобразования Лапласа к (1.2) при начальных нулевых условиях. Здесь s -комплексная переменная. Связь между операторной (1.2) и комплексной (1.3) передаточными функциями можно записать в виде

.

Комплексные числа, являющиеся корнями многочлена В (s), называются нулями передаточной функции, а корни многочлена A (s) – полюсами.

Явный вид связи входа и выхода определяется выражением:

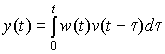, (1.4)

где w (t) – оригинал (т.е. полученный с помощью обратного преобразования Лапласа) комплексной передаточной функции W (s).

Динамические свойства систем характеризуют реакции на входные воздействия специального вида. В частности анализ выхода системы на единичный скачок и d -функцию (дельта-функцию).

Пусть u (t) = 1(t), то есть на вход системы подается функция Хевисайда (единичный скачок), определяемая

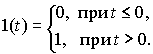
График функции Хевисайда приведен на рис. 1.1. Реакция САУ на единичный скачек называется переходной функцией системы и обозначается h (t).

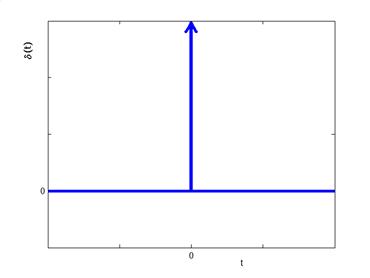
Рис. 1.1. Функция Хевисайда. Рис. 1.2. Функция Дирака.

Если u (t) = d (t), то есть на вход системы поступает функция Дирака (d -функция, импульсная функция, рис. 1.2) определяемая

то реакция САУ называется импульсной переходной функцией системы и обозначается w (t). Таким образом оригинал комплексной передаточной функции можно измерить как реакцию систему на импульс.

Импульсная и переходная функции системы связаны соотношением (из (1.4)):

.

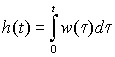Благодаря широкому применению при исследовании устойчивости динамических систем и проектировании регуляторов получили распространение частотные характеристики.

Пусть на вход системы с передаточной функцией W (s) подается гармонический сигнал

u (t) = a_u cos(w t), t >0. (1.5)

В этих условиях справедлива следующая теорема:

Если звено является устойчивым, то установившаяся реакция y (t) на гармоническое воздействие является функцией той же частоты с амплитудой

a_y = a_u | W (iw)|,

и относительным сдвигом по фазе

y = arg W (iw).

Таким образом, выход определяется гармонической функцией

y (t) = a_u | W (iw)| cos(w t + arg W (iw)),

где i – комплексная единица (i ² = –1), 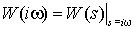– частотная характеристика.

Частотной характеристикой W (iw) стационарной динамической системы называется преобразование Фурье переходной функции:

,

где w (t – t) – импульсная переходная функция.

Связь между комплексной передаточной функцией и частотной характеристикой, исходя из свойств преобразований Фурье можно представить в виде соотношения:

.

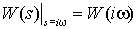При фиксированном значении w частотная характеристика является комплексным числом, и, следовательно, может быть представлена в виде

.

Здесь

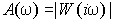– амплитудно-частотная характеристика (АЧХ);

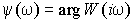– фазово-частотная характеристика (ФЧХ);

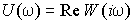– вещественная частотная характеристика (ВЧХ);

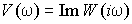– мнимая частотная характеристика (МЧХ).

Геометрическое место точек W (iw) на комплексной плоскости при изменении w от w ₀ до от w ₁ (обычно w ₀ = 0, w ₁ = ¥), называется амплитудно-фазовой характеристикой (АФХ) или частотным годографом Найквиста.

Имеет широкое практическое значение диаграмма Боде (логарифмическая амплитудная характеристика, ЛАХ), которая определяется как L = 20 lg A(w), измеряется в децибелах и строится как функция от lg w.

 

12	Поделиться:

Воспользуйтесь поиском по сайту: