Последовательность выполнения работы

Для выполнения лабораторной работы используется пакет прикладных программ (ППП) Control System Toolbox. ППП предназначен для работы с LTI-моделями (Linear Time Invariant Models) систем управления.

В Control System Toolbox имеется тип данных, определяющих динамическую систему в виде комплексной передаточной функции. Синтаксис команды, создающий LTI-систему c одним входом и одним выходом в виде передаточной функции:

TF([b_m, …, b₁, b₀], [a_n, …, a₁, a₀])

b_m, …, b₁ – значения коэффициентов полинома В в (1.3),

a_n, …, a₁ – значения коэффициентов полинома A в (1.3).

Для выполнения работы могут применяться команды, приведенные в таблице 1.1.

Таблица 1.1. Некоторые команды

Control System Toolbox

Синтаксис	Описание
pole(<LTI-объект>)	Вычисление полюсов передаточной функции
zero(<LTI-объект>)	Вычисление нулей передаточной функции
step(<LTI-объект>)	Построение графика переходного процесса
impulse(<LTI-объект>)	Построение графика импульсной переходной функции
bode(<LTI-объект>)	Построение логарифмических частотных характеристик (диаграммы Боде)
nyquist(<LTI-объект>)	Построение частотного годографа Найквиста

Для определения корней полиномов степени k, может, также, применятся команда MATLAB

roots(P),

которая, в качестве аргумента P, получает матрицу коэффициентов полинома [ p_k, …, p ₀].

Другим вариантом получения графиков динамических характеристик САУ является использование графического интерфейса ППП CST – LTI viewer, вызов которого осуществляется командой

ltiview

которой, в качестве параметра, можно указать имя переменной, содержащей LTI-объект.

Таким образом, выполнение лабораторной работы состоит из следующих шагов:

1. Изучить теоретические сведения.

2. Запустить систему MATLAB.

3. Создать tf-объект, в соответствии с заданным вариантом.

4. Составить дифференциальное уравнение, определяющее функционирование САУ.

5. Определить полюса передаточной функции с использованием команды roots или pole.

6. Определить нули передаточной функции с использованием команды roots или zero.

7. Используя LTI-viewer, или соответствующие команды (табл.1) получить динамические характеристики – переходную функцию h (t), импульсно-переходную функцию w (t) и частотные характеристики – диаграмму Боде, частотный годограф Найквиста.

8. Получить представление исходной функции в виде произведения типовых звеньев.

9. Ответить на контрольные вопросы.

10. Оформить отчет.

11. Сдать отчет преподавателю и защитить работу.

Примечание: Варианты заданий, состоят из двух цифр: первая - номер передаточной функции, вторая – номер набора значений коэффициентов.

 

Методический пример

Задана передаточная функция САУ

.

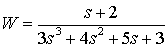Найдем ее динамические и частотные характеристики. Будем работать в командном режиме среды MATLAB.

1. Создадим LTI-объект с именем w, для этого выполним:

2. Найдем полюса и нули передаточной функции с использованием команд pole, zero.

3. Построим переходную функцию командой step(w). Результат ее выполнения приведен на рис. 1.3.

Рис. 1.3. Переходная функция h(t).

4. Построим импульсную переходную функцию командой impulse(w). Результат показан на рис. 1.4.

Рис. 1.4. Импульсная переходная функция.

5. Диаграмму Боде получим, используя команду bode(w) – рис. 1.5.

Рис. 1.5. Логарифмические частотные характеристики.

6. Определим частотный годограф Найквиста, выполнив команду nyquist(w) – рис. 1.6.

Рис. 1.6. Частотный годограф.

Аналогичные результаты (рис. 1.7) можно получить, используя команду ltiview(w), с соответствующими настройками в меню “Plot Configuration”.

Рис. 1.7. LTI-viewer.

Каждая из построенных характеристик полностью и однозначно определяет рассматриваемую систему управления.

 

Варианты заданий

№	Вид передаточной функции	№	Коэффициенты полиномов
			b 0	b 1	a 0	a 1	a 2	a 3	а 4
1.		1.
2.
3.		-3
4.
5.			-2	-2	-3	-2
			b 0	b 1	b 2	a 0	a 1	a 2	а 3
2.		1.		-3
2.			-3	-4	-6	-4	-1
3.	-4		-2
4.		-8	-7		-6	-3	-1
5.		-1	-3	-1		-7	-2
			b 0	b 1	b 2	a 0	a 1	a 3	a 4
3.		1.				-3		-7
2.	-5			-8	-2	-1	-6
3.	-7
4.	-6		-4
5.		-2	-1
4.		1.		-5
2.		-6
3.	-2	-8
4.	-7	-1
5.	-3		-4
			b 2	b 3	a 0	a 1	a 2	a 3	a 4
5.		1.		-5
2.		-6
3.	-2	-8
4.	-7	-1
5.	-3		-4

 

Контрольные вопросы

1. Представьте систему в виде последовательного соединения типовых звеньев.

2. Дайте определение и поясните физический смысл переходной функции.

3. Представьте исходную систему в пространстве состояний.

4. Найдите передаточную функцию замкнутой системы.

5. Постройте динамические характеристики типовых звеньев.

6. Определите вид ЛЧХ для пропорционально – интегрально –дифференциального регулятора.

 

 

12	Поделиться:

Воспользуйтесь поиском по сайту: