 |
Наращение и выплата процентов в потребительском кредите
|
|
|
|
В потребительском кредите проценты, как правило, начисляются на всю сумму кредита и присоединяются к основному долгу уже в момент кредита. Такой метод называется разовым начислением процентов. Погашение долга с процентами производится частями (обычно равными суммами) на протяжении всего срока кредита:
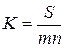, (3.5)
где n - срок кредита; m - число платежей в году.
Дисконтирование и учет по простым процентным ставкам
Термин дисконтирование употребляется как средство определения
любой стоимостной величины, относящейся к будущему, на некоторый, более ранний момент времени.
В финансовой практике часто сталкиваются с задачей, обратной наращению процентов: по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды P. Такая ситуация может возникнуть, например при разработке условий контракта. Расчет P по S необходим и тогда, когда проценты с суммы S удерживаются вперед, т.е. непосредственно при выдаче ссуды. В этом случае говорят, что сумма S дисконтируется или учитывается, сам процесс начисления процентов и их удержание называется учетом, а удержанные проценты - дисконтом. В зависимости от вида процентной ставки применяют два метода дисконтирования - математическое дисконтирование и банковский (коммерческий) учет. В первом случае используется ставка наращения, во втором - учетная ставка.
Математическое дисконтирование представляет собой формальное решение задачи, обратной наращению первоначальной суммы ссуды.
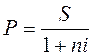, (3.6)
, (3.7)
где D - дисконта.
Банк или иное финансовое учреждение до наступления срока платежа по векселю или иному платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.е. покупает (учитывает) его с дисконтом (т.е. со скидкой). Получив при наступлении срока векселя деньги, банк реализует дисконт. При учете векселя применяется банковский или коммерческий учет, согласно этому методу проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уплате в конце срока. При этом применяется учетная ставка d.
|
|
|
, (3.8)
Для ставки наращения прямой задачей является определение наращенной суммы, обратной - дисконтирование. Для учетной ставки, наоборот, прямая задача заключается в дисконтировании, обратная - в наращении.
Ставка Прямая задача Обратная задача
i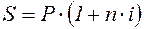 
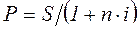(3.9)
d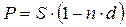 
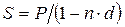
Учетная ставка отражает фактор времени более жестко. Например, при d = 20 % уже 5-ти летний срок достаточен для того, чтобы владелец векселя ничего не получил при его учете.
Определение срока ссуды и величины процентной ставки
Необходимые для расчета продолжительности ссуды в годах и днях по-
лучим, решив уравнения (3.1) и (3.8) относительно n:
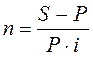, (3.10) 
, (3.11)
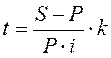, (3.12) 
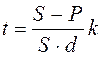, (3.13)
По этим же уравнениям можно определить и процентные ставки:
, (3.14) 
, (3.15)
Сложные проценты
В средне и долгосрочных финансово-кредитных операциях применяют сложные проценты. База для начисления сложных процентов (в отличие от простых) не остается постоянной - она увеличивается с каждым шагом во времени, абсолютная сумма начисляемых процентов возрастает, и процесс увеличения суммы долга происходит с ускорением. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называют капитализацией процентов.
Наращенная сумма по сложным процентам вычисляется по уравнению:
, (3.16)
где S - наращенная сумма;
P - первоначальный размер долга (ссуда, кредит и т.д.);
i - процентная ставка;
n - число лет наращения.
Пример: Какой величины достигнет долг, равный 1 млн. руб., через пять лет при росте по сложной ставке 15,5% годовых?
|
|
|
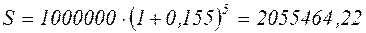руб.
Различия в последствиях применения простых и сложных процентов
наиболее наглядно проявляется при определении времени, необходимого для увеличения первоначальной суммы в N раз.
Для простых процентов:
, (3.17)
Для сложных процентов:
, (3.18)
Пример. Определим число лет, необходимого для увеличения первоначального капитала в пять раз, применяя сложные и простые % по ставке 15% годовых.
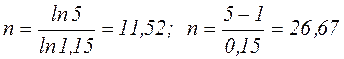
Номинальная ставка
В современных условиях проценты капитализируются не один, а несколько раз в году - по полугодиям, кварталам и т.д. Некоторые зарубежные коммерческие банки практикуют даже ежедневные начисления процентов. При начислении % несколько раз в году можно воспользоваться формулой (3.16), параметр n в этих условиях будет означать число периодов начисления, а под ставкой i следует понимать ставку за соответствующий период. В контрактах фиксируется не ставка за период, а годовая ставка в % и указывается период начисления %.
Пусть годовая ставка равна j, а число периодов начисления в году равно m. Проценты начисляют по ставке j/m. Ставку j называют номинальной.
Формулу наращения можно представить следующим образом:
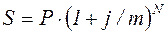, (3.19)
Пример: Какова сумма долга через 25 месяцев, если первоначальная
величина 500 тыс. руб., проценты сложные, ставка 20 % годовых, начисляются поквартально.
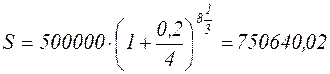руб.
Эффективная ставка
Эффективная ставка - это годовая ставка сложных процентов, которая дает тот же результат, что и m-разовое начисление процентов по ставке 
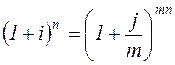
откуда
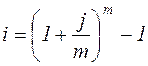, (3.20)
При m>1, эффективная ставка (i) больше номинальной (j) при m=1; i=j.
Замена в договоре номинальной ставки j при m-разовом начислении процентов на эффективную ставку i не изменяет финансовых обязательств участвующих сторон т.е. обе ставки эквивалентны в финансовом отношении.
Пример. Какова эффективная ставка, если номинальная ставка равна 25 % при помесячном начислении процентов?
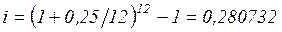
Для сторон в сделке безразлично: применить ставку 25 % (при помесячном начислении) или годовую ставку 28,0732 %.
При подготовке контрактов может возникнуть необходимость и в решении обратной задачи - в определении j по заданным значениям i и m. Находим:
|
|
|
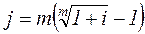, (3.21)
|
|
|
