Алгоритм обработки результатов прямых измерений

Алгоритм обработки результатов косвенных измерений

1. Обрабатываем Х_i по ГОСТ 8.207. Найти среднее значение величин входящих в формулу х_ср.1 х_ср2.
2. Исключаем промахи:-3σ_i < X_max,min – X_cp < 3σ_i
3. Найти среднее значение измеряемой величины по известной функциональной зависимости У_ср = f(_Xсрi)
4. У_ср = f(X_i)
5. Случайная погрешность:

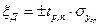
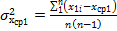
1. Систематическая суммарная погрешность:

k_0,9 = 0,95; k_0,95 = 1,1; k_0,99 = 1,4

Для равномерного распределения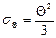

1. Абсолютная погрешность:

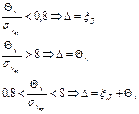
1. Относительная погрешность:
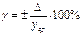
2. Окончательный результат: Y = (Y_cp 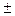Δ) ед., при Р_Д = …, n = …

 

Алгоритм обработки результатов прямых измерений

При статистической обработке группы результатов наблюдений следует выполнить следующие операции:

1. Исключить известные систематические погрешности из результатов наблюдений

2. Вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения

3. Вычислить оценку среднего квадратического отклонения результата наблюдения

4. Вычислить оценку среднего квадратического отклонения результата измерения

5. Проверить гипотезу о том, что результаты наблюдений принадлежат нормальному распределению

6. Вычислить доверительные границы случайной погрешности (случайно - составляющей погрешности) результата измерения

7. Вычислить границы неисключенной систематической погрешности (неисключенных остатков систематической погрешности) результата измерения

8. Вычислить доверительные границы погрешности результата измерения

Проверку гипотезы о том, что результаты наблюдений принадлежат нормальному распределению, следует проводить с уровнем значимости q от 10 до 2 %. Конкретные значения уровней значимости должны быть указаны в конкретной методике выполнения измерений.

Для определения доверительных границ погрешности результата измерения доверительную вероятность P принимают равной 0,95.

В тех случаях, когда измерение нельзя повторить, помимо границ, соответствующих доверительной вероятности P=0,95,допускается указывать границы для доверительной вероятности P=0,99.

В особых случаях, например при измерениях, результаты которых имеют значение для здоровья людей, допускается вместо P= 0,99 принимать более высокую доверительную вероятность.

Среднее квадратическое отклонение σ результата наблюдения оценивают согласно НТД.

Среднее квадратическое отклонение σ(Ã) результата измерения оценивают по формуле:

S(х_ср) = √∑(Xi- Х_ср) ² / n(n-1)

Где Xi - i-ый результат наблюдения

Х_ср - результат измерения (ср.арифметическое исправленных результатов наблюдений)

n - число результатов наблюдений

S(х_ср) - оценка среднего квадратического отклонения результата измерения.

2. 1.Определяем x среднее

2.Находим СКО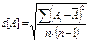

3. Исключаем промахи:-3σ_i < X_max,min – X_cp < 3σ_i

4. Проверяем гипотезу о соответствии распределения нормальному закону.

5. Вычисляем доверительные границы погрешности рез-тата.

6. Определяем границы неисключенных систематических погрешностей рез-тата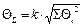

k=1,1 при Р=0,95. Систематическая инструментальная погрешность, определяется по классам точности СИ. Необходимо записать систематическую погрешность СИ в абсолютной форме, в простейшем случае Q =D_си, Q = ± g × Х_к/100%, g - погрешность прибора; Х_к – верхняя граница диапазона измерений.

7. В случае, если 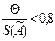, то неисключенными систематическими погрешностями по сравнению со случайными пренебрегают и принимают, что граница погрешности результата 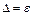. Если 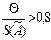, то случайной погрешностью по сравнению с систематическими пренебрегают и принимают, что граница погрешности результата .

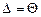8. Записывают результат: х = 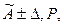=, n =

 

12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: