Уравнение прямой, проходящей через данную точку, в данном направлении

Лекция № 4

Простейшие задачи аналитической геометрии на плоскости. Уравнения прямой на плоскости

Расстояние между точками на плоскости

Пусть на плоскости даны две точки и .Найдем расстояние между двумя точками.

у

 

 

x

Pис.1

 

Из треугольника АВС имеем (рис.1):

Так как , то, обозначив получим . (1.1)

 

Деление отрезка в данном отношении

Даны точки и . Пусть точка делит отрезок в отношении т.е. .

у

х

Рис.2

 

На основании теоремы о пропорциональности отрезков прямых, заключенных между параллельными прямыми (рис.2) имеем:

, где

Тогда будем иметь: .

Решив это уравнение, получим:

(1.2)

Аналогично рассуждая найдем,

(1.3)

Если точка С является серединой отрезка, то её координаты можно вычислить по формулам:

; (1.4)

 

Пример: Даны точки и . На прямой АВ найти точку С, которая делит отрезок АВ в отношении 2:3 и находится между точками А и В.

Решение: , 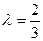Применяя формулы (1.2) и (1.3) найдем

.

То есть искомая точка имеет координаты .

 

3.Вычисление площади треугольника

Пусть на плоскости даны две точки , и . Найдем площадь S треугольника АВС.

у

В

 

 

А

С

 

х

Рис.3

 

Построим проекции точек А, В и С на ось ОХ, получим точки , и .

Из рисунка видно, что площадь искомого треугольника будет равна:

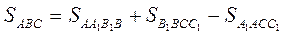
Тогда

. (1.5)

Если при вычислении значение определителя получается равным нулю, то это означает, что точки А,В и С лежат на одной прямой. Если значение определителя получается отрицательным, то следует взять его модуль.

Пример:Даны точки , и . Найти площадь треугольника АВС.

Решение: Применяя формулу (1.5) получим:

(кв.ед.)

 

Уравнение линии

 

Уравнением линии на плоскости ХОУ называется такое уравнение с двумя переменными, которому удовлетворяют координаты х и у каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Переменные х и у в уравнении линии называются текущими координатами точек линии.

 

Прямая как линия первого порядка

Простейшей из линий является прямая.

Чтобы составить уравнение прямой линии в декартовых координатах нужно каким-то образом задать условие, определяющее положение ее относительно координатных осей.

Назовем углом наклона прямой к оси Ох угол , на который надо повернуть эту ось, чтобы она совпала с данной прямой.

Припишем углу знак плюс при повороте оси Ох против часовой стрелки, знак минус при повороте Ох по ходу часовой стрелки.

Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой.

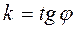(2.1)

Угловой коэффициент характеризует направление прямой по отношению осей координат.

В частности, если , то и . В этом случае прямая параллельна оси Ох, если = , то не существует, т.е. прямая перпендикулярна оси Ох.

 

Уравнение прямой линии с угловым коэффициентом

Пусть дана некоторая прямая, составляющая угол с осью Ох, и отсекающая на оси Оу отрезок, по величине равный b. Возьмем на данной прямой произвольную точку , точка - точка пересечения прямой с осью Оу. Когда точка М движется по прямой, то ее координаты х и у изменяются, и остаются все время связанными между собой некоторым условиям.

Установим это условие: рассмотрим отрезок NM. Зная координаты точек и , найдем угловой коэффициент прямой, выразив его через координаты этих точек.

у

 

 

P

 

х

x

Рис.4

 

Из прямоугольного треугольника (рис.4) получим

.

Так как 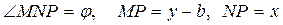, то

,

или (2.2)

 

Уравнение прямой вида (2.2) называется уравнением прямой с угловым коэффициентом.

Если прямая параллельна оси ОХ, то угол наклона прямой к оси ОХ равен нулю , значит . Тогда уравнение (2.2) примет вид

. (2.3)

Любая точка этой прямой имеет ординату, равную b.

Если прямая параллельна оси ОУ, то 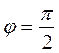, значит не существует. В этом случае уравнение прямой будет иметь вид:

, (2.4)

где а – абсцисса точки пересечения прямой с осью ОХ.

Любая точка этой прямой имеет абсциссу, равную а.

Если прямая проходит через начало координат, то . Тогда уравнение прямой будет иметь вид:

(2.5)

 

Пример 1. Составить уравнение прямой, образующей с осью ОХ угол и пересекающей ось ОУ в точке (0;-6).

Решение. Здесь , значит . Величина отрезка, отсекаемого на оси ОУ равна .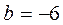

Следовательно, искомое уравнение получим в виде:

.

 

Пример 2. Найти уравнение прямой параллельной оси ОХ и отсекающей на оси ОУ отрезок, равный 2.

Решение. Здесь , значит . Величина отрезка, отсекаемого на оси ОУ равна .

Следовательно, искомое уравнение получим в виде:

.

Уравнение прямой, проходящей через данную точку, в данном направлении

Пусть дана точка на прямой и угол наклона этой прямой к оси ОХ. Возьмем произвольную точку на прямой, которая проходит через точку .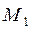

Уравнение этой прямой будем искать в виде (2.2) , где неизвестное определится из условия прохождения прямой через точку 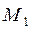, т.е. , отсюда .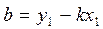

Подставим найденное значение b в уравнение (2.2), получим:

или

(2.6)

Это и есть уравнение прямой, проходящей через данную точку в данном направлении.

Полученное уравнение также называют уравнением пучка прямых (множества) прямых, проходящих через данную точку, так как задавая различные значения углового коэффициента k, мы можем получить множество прямых, проходящих через точку – центр пучка. В форме (2.6) можно записать любое уравнение пучка, кроме прямой параллельной оси ОУ.

Пример. Составить уравнение прямой, проходящей через точку (-5,6), и наклоненной к оси ОХ под углом =135⁰.

Решение. Здесь . Находим угловой коэффициент прямой: .

Используя формулу (2.6) будем иметь:

или .

 

12	Поделиться:

Воспользуйтесь поиском по сайту: