 |
Уравнение прямой, проходящей через две точки
|
|
|
|
Пусть даны точки 
и 
. Составим уравнение прямой, проходящей через эти две точки.
Уравнение пучка прямых, проходящих через точку имеет вид 
где неизвестный коэффициент k определим из условия прохождения прямой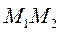 
через точку , т.е. координаты точки 
должны удовлетворять уравнению (2.6):
отсюда
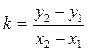(2.7).
Подставляя (2.7) в (2.6), получим:
(2.8)
Это и есть искомое уравнение прямой, проходящей через две данные точки.
Пример 1. Составить уравнение прямой линии, проходящей через точки 
и 
.
Решение. Здесь 
. Подставим эти значения в (2.8):
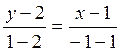, отсюда 
.
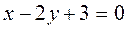Пример 2. Составить уравнение медианы ВЕ в треугольнике АВС, если 
.
Решение. Как ВЕ – медиана, то точка Е является серединой отрезка АС. Поэтому координаты точки Е найдем по формулам (1.4)
; 
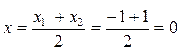Т.е. точка Е имеет координаты: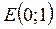 
.
Для составления уравнение медианы воспользуемся теперь уравнением прямой, проходящей через две точки
Получим:
.
Окончательно уравнение медианы получим в виде:
Угол между двумя прямыми
Пусть две прямые заданы своими уравнениям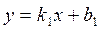и 
и 
. Будем называть одну из них первой (какую угодно), другую – второй.
Обозначим через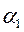 
угол наклона первой прямой к оси ОХ, через 
- угол наклона второй прямой. Для определенности будем считать, что 
.
у (2)
(1)
х
Рис.5
В этом случае угол между прямыми (1) и (2) будет равен 
Тогда имеем: 
где 
и 
, следовательно
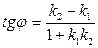(2.9)
Это есть формула для определения угла между двумя прямыми.
При решении различных задач часто возникают вопросы об установлении параллельности или перпендикулярности двух прямых на плоскости.
Очевидно, что две прямые параллельны тогда и только тогда, когда углы наклона к оси ОХ двух прямых равны друг другу, т.е.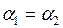 
, следовательно 
.
|
|
|
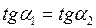Отсюда: 
(2.10)
Это и есть условие параллельности двух прямых на плоскости.
Если данные прямые перпендикулярны, т.е. 
, тогда 
теряет арифметический смысл, в этом смысле знаменатель правой части (2.9) должен быть равен нулю 
.
Следовательно, признаком перпендикулярности двух прямых является равенство:
, или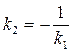 
(2.11)
Пример 1. Найти угол между прямыми 
и 
.
Решение. Если перенумеровать прямые в том порядке, как они заданы, то угловой коэффициент первой прямой 
, а для второй прямой 
.
Тогда по формуле (2.9) получим: 
.
Значит, угол между данными прямыми равен 
= 450.
Пример 2. Составить уравнение прямой линии, проходящей через точку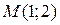 
параллельно прямой 
.
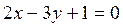Решение. Угловой коэффициент данной прямой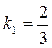 
. Из условия параллельности прямых (2.10) угловой коэффициент прямой, для которой нужно составить уравнение будет также равен 
. Используя уравнение (2.6) получим:
или 
Окончательно будем иметь 
.
Пример 3. Составить уравнение прямой, проходящей через точку 
перпендикулярно к прямой 
.
Решение. Угловой коэффициент данной прямой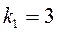 
. Искомый угловой коэффициент 
находим из условия перпендикулярности
, т.е. 
.
Используя уравнение пучка прямых получим
Окончательно уравнение искомой прямой будет иметь вид:
.
Общее уравнение прямой
Анализ уравнений (2.2), (2.6) и (2.8) показывает, что уравнения прямой описываются уравнениями первой степени относительно переменных х и у, поэтому общее уравнение прямой можно записать в виде:
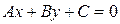(2.12).
Преобразуем это уравнение к виду уравнения прямой в угловым коэффициентом: 
Т.е. угловой коэффициент прямой, заданной в общем виде, можно вычислить по формуле: 
Рассмотрим три частных случая, когда уравнение первой степени будет неполным:
1) С = 0, тогда (2.12) примет вид 
Это уравнение определяет прямую, проходящую через начало координат.
2) В = 0, уравнение (2.12) примет вид
|
|
|
или 
, где 
Это уравнение определяет прямую, параллельную оси ОУ.
В частности, если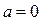 
, то уравнение 
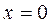определяет прямую, которая совпадает с осью ОУ.
3) А = 0, тогда общее уравнение прямой будет иметь вид
или 
, где 
.
Это уравнение прямой параллельной оси ОХ.
В случае, если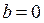 
, то уравнение 
является уравнением оси ОХ
|
|
|
12 |
