 |
Шкалы измерений и уравнения измерений
|
|
|
|
Шкалы
Термин "шкала" в метрологической практике имеет, по крайней мере, два различных значения. Во-первых, шкалой или точнее шкалой измерений называют принятый по соглашению порядок определения и обозначения всевозможных проявлений (значений) конкретного свойства (величины). Во-вторых, шкалой называют отсчетные устройства аналоговых средств измерений. В настоящей рекомендации термин "шкала" используется только в первом из приведенных выше значений.
Измерению подлежат различные проявления свойств тел, веществ, явлений, процессов. Некоторые свойства при этом проявляются количественно (длина, масса, температура и т.п.), а другие - качественно (например, цвет, т.к. не имеет смысла выражение типа "красный цвет больше (меньше) синего"). Многообразие (количественное или качественное) проявлений любого свойства образуют множества, отображение элементов которых на упорядоченные множества чисел или, в более общем случае, на систему условных знаков образуют шкалы измерения этих свойств. Такими системами знаков являются, например, множество обозначений (названий) цветов, совокупность классификационных символов или понятий, множество баллов оценки состояний объекта, множество действительных чисел и т.д. Элементы множеств проявления свойств находятся в определенных логических соотношениях между собой. Такими соотношениями могут быть "эквивалентность" (равенство) или "сходство" (близость) этих элементов, их количественная различимость ("больше", "меньше"), допустимость выполнения определенных математических операций сложения, вычитания, умножения деления с элементами множеств и т. д. Эти особенности элементов множеств проявления свойств определяют типы (особенности соответствующих им шкал измерений).
|
|
|
В соответствии с логической структурой проявления свойств в теории измерений различают пять основных типов шкал измерений: наименований, порядка, разностей (интервалов), отношений и абсолютные шкалы. Каждый тип шкалы обладает определенными признаками, основные из которых рассматриваются ниже.
ШКАЛЫ НАИМЕНОВАНИЙ отражают качественные свойства. Их элементы характеризуются только соотношениями эквивалентности (равенства) и сходства конкретных качественных проявлений свойств. Примерами таких шкал является шкала классификации (оценки) цвета объектов по наименованиям (красный, оранжевый, желтый, зеленый и т.д.), опирающаяся на стандартизованные атласы цветов, систематизированные по сходству. В таких атласах, выполняющих роль своеобразных эталонов, цвета могут обозначаться условными номерами (координатами цветами). Измерения в шкале цветов выполняются путем сравнения при определенном освещении образцов цвета из атласа с цветом исследуемого объекта и установления эквивалентности их цветов.
В шкалах наименований нельзя ввести понятия единицы измерения; в них отсутствует и нулевой элемент.
Шкалы наименований, по существу, качественны; однако возможны некоторые статистические операции при обработке результатов измерений в этих шкалах, например, можно найти модальный или наиболее многочисленный класс эквивалентности.
ШКАЛЫ ПОРЯДКА - описывают свойства, для которых имеют смысл не только соотношения эквивалентности, но и соотношения порядка по возрастанию или убыванию количественного проявления свойства. Характерным примером шкал порядка являются существующие шкалы чисел твердости тел, шкалы баллов землятрясений, шкалы баллов ветра, шкала оценки событий на АЭС и т.п. Узкоспециализированные шкалы порядка широко применяются в методах испытаний различной продукции.
|
|
|
В этих шкалах также нет возможности ввести единицы измерений из-за того, что они не только принципиально нелинейны, но и вид нелинейности может быть различен и неизвестен на разных ее участках. Результаты измерений в шкалах твердости, например, выражаются в числах твердости по Бринеллю, Виккерсу, Роквеллу, Шору, а не в единицах измерений. Шкалы порядка допускают монотонные преобразования, в них может быть или отсутствовать нулевой элемент.
ШКАЛЫ РАЗНОСТЕЙ (ИНТЕРВАЛОВ) - отличаются от шкал порядка тем, что для описываемых ими свойств имеют смысл не только соотношения эквивалентности и порядка, но и суммирования интервалов (разностей) между различными количественными проявлениями свойств. Характерный пример - шкала интервалов времени.
Интервалы времени (например, периоды работы, периоды учебы) можно складывать и вычитать, но складывать даты каких-либо событий бессмысленно.
Другой пример, шкала длин (расстояний) пространственных интервалов определяется путем совмещения нуля линейки с одной точкой, а отсчет делается у другой точки. К этому типу шкал относятся и шкалы температур по Цельсию, Фаренгейту, Реомюру.
Шкалы разностей имеют условные (принятые по соглашению) единицы измерений и нули, опирающиеся на какие-либо реперы.
В этих шкалах допустимы линейные преобразования, в них применимы процедуры для отыскания математического ожидания, стандартного отклонения, коэффициента ассиметрии и смещенных моментов.
ШКАЛЫ ОТНОШЕНИЙ. К множеству количественных проявлений в этих шкалах применимы соотношения эквивалентности и порядка - операции вычитания и умножения, (шкалы отношений 1-го рода - пропорциональные шкалы), а во многих случаях и суммирования (шкалы отношений 2-го рода - аддитивные шкалы).
В шкалах отношений существуют условные (принятые по соглашению) единицы и естественные нули. Примерами шкал отношений являются шкалы массы (2-го рода), термодинамическая температурная шкала (1-го рода).
Массы любых объектов можно суммировать, но суммировать температуры разных тел нет смысла, хотя можно судить о разности и, отношении их термодинамических температур. Шкалы отношений широко используются в физике и технике, в них допустимы все арифметические и статистические операции.
|
|
|
АБСОЛЮТНЫЕ ШКАЛЫ - обладают всеми признаками шкал отношений, но дополнительно в них существует естественное однозначное определение единицы измерений. Такие шкалы используются для измерений относительных величии (отношений одноименных величин: коэффициентов усиления, ослабления, КПД, коэффициентов отражений и поглощений, амплитудной модуляции и т.д.).
ЛОГАРИФМИЧЕСКИЕ ШКАЛЫ - логарифмическое преобразование шкал, часто применяемое на практике, приводит к изменению типа шкал. Практическое распространение получили логарифмические шкалы на основе применения систем десятичных и натуральных логарифмов, а также логарифмов с основанием два.
Логарифм есть число безразмерное, поэтому перед логарифмированием преобразуемая размерная величина в начале обращается в безразмерную путем ее деления на принятое по соглашению произвольное (опорное) значение той же величины, после чего выполняется операция логарифмирования.
В зависимости от типа шкалы, подвергнутой логарифмическому преобразованию, логарифмические шкалы могут быть двух видов. При логарифмическом преобразовании абсолютных шкал получаются абсолютные логарифмические шкалы, называемые иногда логарифмическими шкалами с плавающим нулем, т.к. в них не фиксируется опорное значение. Примерами таких шкал являются шкалы усиления (ослабления) сигнала в дБ. Для значений величин в абсолютных логарифмических шкалах допустимы операции сложения и вычитания.
При логарифмическом преобразовании шкал отношений и интервалов получается логарифмическая шкала интервалов с фиксированным нулем, соответствующим принятому опорному значению преобразуемой шкалы. В радиотехнике в качестве опорного чаще всего принимают значения 1 мВт, 1 В, 1 мкВ; в акустике - 20 мкПа и др. К этим шкалам в общем случае нельзя прямо применять ни одно арифметическое действие; сложение и вычитание величин, выраженных в значениях таких шкал, должно проводиться путем нахождения их антилогарифмов, выполнения необходимых арифметических операций и повторного логарифмирования результата.
|
|
|
БИОФИЗИЧЕСКИЕ ШКАЛЫ. В метрологической практике существует ряд шкал, которыми описываются реакции биологических объектов, прежде всего человека, на воздействующие на них физические факторы. К ним относятся шкалы световых и цветовых измерений, шкалы восприятия звуков, шкалы эквивалентных доз ионизирующих излучений и др. Будем называть такие шкалы биофизическими.
Биофизическая шкала - шкала измерений свойств физического фактора (стимула), модифицированная таким образом, чтобы по результатам измерений этих свойств можно было прогнозировать уровень или характер реакции биологического объекта на действие этого фактора. Такие шкалы строятся по моделям, так модифицирующим (трансформирующим) результаты измерений свойства стимула, чтобы было однозначное соответствие между результатом измерений и характеристикой биологической реакции (гомоморфное отображение множества стимулов на множество реакций). При этом некоторому подклассу множества стимулов могут соответствовать эквивалентные реакции.
Такая модифицированная шкала стимулов, естественно, по логической структуре приближается к структуре шкалы реакций и приобретает некоторую прогностическую ценность.
Однако, как правило, биофизическая шкала стимулов и шкала соответствующих реакций являются шкалами разных типов, поэтому на прогностические суждения о реакциях, вызываемых стимулами, нельзя прямо переносить логические соотношения шкалы стимулов. Так, например, шкала яркостей с точки зрения стимулов является неограниченной аддитивной шкалой отношений, а с точки зрения восприятия человеком - шкалой порядка в ограниченном снизу и сверху диапазоне значений стимулов.
Уравнения
Основное уравнение измерений имеет вид:
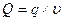
Q — измеряемая физическая величина;
q — её числовое представление в принятых единицах измерения физической величины Q;
υ — принятая единица измерения физической величины Q.
|
|
|


