Энтропийное представление о количестве измерительной информации

В понятии теории информации смысл измерения состоит в сужении интервала неопределенности. При практическом использовании информационного подхода для оценки точности результатов измерений рационально оперировать с понятием энтропийного значения погрешности Δ_э.

Можно оценивать погрешность через число разрешаемых градаций отклика. Так, имея шкалу, проградуированную в определенных единицах величины, затруднительно решить вопрос об измеренном значении этой величины, если точка (показание прибора) попадает между делениями шкалы.

Вопрос можно решить 2-мя путями: увеличить количество градаций, уменьшив цену деления (тогда более точно можно будет сказать, что это две разные точки), или воспользоваться энтропийным подходом, заключающимся в оценке количества получаемой информации. Энтропия – мера неопределенности. Согласно К.Шенноу, количество информации I, определяется как разность энтропий:

I = H(X) – H(X/X_п),

где H(X) – энтропия измеряемой величины до ее измерения;

H(X/X_п) – (энтропия Х при условии Х_п) – энтропия действительного значения х измеряемой величины вокруг показания Х_{п ,} полученного после измерения, т.е. энтропия погрешности измерения.

Эти оценки неопределенности в виде энтропии до и после измерения могут быть вычислены по соотношению:

Пример. Пусть для измерения вели­чины х был использован прибор со шкалой от X₁ до Х₂, (например, амперметр со шкалой от —50 А до +50 А). Тогда вероятностное описание ситуации до измерения состоит в том, что вероятность получить показания прибора в интервалах от —∞ до Х₁ и от Х₂ до +∞ равна нулю, т. е. плотность распределения вероятностей р(х) в этих интервалах также равна нулю. Следовательно, пока­зание можно ожидать лишь в интервале от Х₁ до Х₂ и, если пред­положить, что оно с равной вероятностью может оказаться в лю­бой части этого диапазона, то вероятностное описание ситуации до измерения изобразится равномерным распределением х в пре­делах от Х₁ до Х₂ и может быть запи­сано как

р (х) = l/(Х₂- Х₁) при Х₁≤ х ≤ Х₂;

р (х) = 0 при х < Х₁ и х > Х₂

Отсюда энтропия Н(X) до измерения: 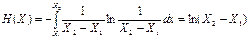. Таким образом, до измерения интервал неопределенности пред­стоящего отсчета простирается от X₁ до Х₂, а шенноновская энтропия есть логарифмическая мера длины этого интервала.

После проведения измерения мы получаем отсчет Х_п. Однако вследствие погрешности прибо­ра, равной ±Δ, можем лишь утверждать, что действительное значение измеряемой величины лежит где-то в пределах интер­вала неопределенности шириной d = 2Δ.. Если прибор обладает погрешностью с равномерным рас­пределением, то ситуация после измерения описывается распре­делением с шириной d = 2Δ и плот­ностью р(х) = 1/(2Δ). Таким образом, в понятиях теории информации смысл измере­ния состоит в сужении интервала неопределен­ности от Х₂ - Х₁ до измерения до d = 2Δ — после измере­ния, т. е. в N = (Х₂ — Х₁)/(2Δ) раз.

Количество информации, полученное в результате измерения, равно разности исходной и оставшейся энтропии, т. е.:

.

Число N показывает, сколько интервалов не­определенности длиной d = 2Δ укладывается во всем диапазоне Х₂ — Х₁ т. е. какое число различимых градаций измеряемой ве­личины позволяет получить данный прибор или метод измерения.

Соотношения I = In N и N = (Х₂ — X₁)/d справедливы при любом законе рас­пределения погрешности, если только интервал неопределен­ности d будет найден через энтропию.

Так, например, для нормально распре­деленной погрешности:

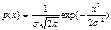
Отсюда энтропия погрешности:

Учитывая, что и по определению дисперсии , получаем 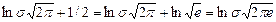, т. е. интервал неопределен­ности d результата измерения, найденный через энтропию в соот­ветствии с теорией информации, однозначно (без каких-либо предположений о выборе уровня доверительной вероятности) равен d = ≈ 4,133σ, а число различимых градаций ре­зультата измерения при равномерном распределении вероятности различных значений измеряемой величины:

.

Подобным же образом энтропийный интервал неопределен­ности результата измерения может быть однозначно найден для любого выраженного аналитически закона распределения погреш­ности.

При практи­ческом использовании информационного подхода для оценки точности результатов измерений привычнее оперировать не со значениями энтропийного интервала неопределенности ре­зультата измерения d, а с половиной этого интервала, присвоив ей наименование энтропийного значения погрешности Δ_э. Формальным определением энтропийного значения случайной величины являются соотношения:

отсюда 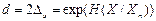и .

Соотношение между энтропийным Δ_э и средним квадратическим σ значениями погрешности различно для разных законов распределения, и его удобно характеризовать значением энтро­пийного коэффициента k =Δ_э/σ данного закона распределения. Для нормального распреде­ления 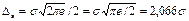и k = 2,066. Для других распределений по-другому. Максимальное возможное значение энтропийного коэффициента k = 2,066 имеет нормальное распределение.

(про энтропийную вероятность я уже понять не в силах. Кому надо, читайте в Новицком, с.60)