Суммирование неисключенных систематических погрешностей

Систематические погрешности, которые остаются в результатах измерения после проведения операций обнаружения, оценки и исключения, называются неисключенными систематическими погрешностями.

При определении границы результирующей неисключенной систематической погрешности ее отдельные составляющие рассматриваются как случайные величины. Если известно, что распределение составляющих неисключенной систематической погрешности нормальное, то

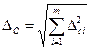(7.3)

 

где 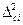- значение неисключенной составляющей систематической погрешности;

m - количество неисключенных систематических погрешностей.

Если данных о виде распределения нет, то

k

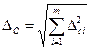(7.4)

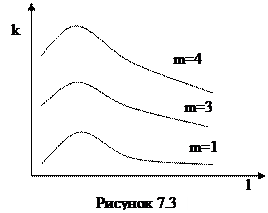При Р_д=0,95 коэффициент k=1,l. При Р_д=0,99 k зависит от числа неисключеных систематических погрешностей m. Если m>4, то k=1,4. При m≤4 поступают следующим образом. Находят отношение 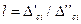, где ∆'_ci - составляющая систематической погрешности, наиболее отличающаяся по своему значению от остальных;

∆”_сi - составляющая систематической погрешности, по своему значению наиболее приближающаяся к ∆'_сi. Затем по графику зависимости k от 1, приведенному на рисунке 7.3, находят значение k. При косвенных измерениях неисключенные систематические погрешности суть частные неисключенные систематические погрешности косвенного измерения:

 

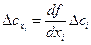(7.5.)

8 РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ

 

Вследствие того, что результат измерения X содержит случайную погрешность , он сам является случайной величиной, так как X=Q+∆.

Основной характеристикой любой случайной величины является функция распределения вероятностей, которая устанавливает связь между возможными значениями случайной величины и вероятностями их появления при многократных измерениях.

Существуют две формы представления случайной величины: интегральная и дифференциальная.

Интегральной функцией распределения результатов наблюдения является функция. F(X) - вероятность того, что результат наблюдения окажется меньше некоторого текущего значения х: F(X)=P{X<x}. Это положительная неубывающая функция. Она имеет вид, представленный на рисунке 8,1.

 

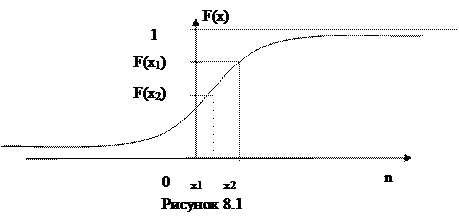Основным свойством этой функции является следующее: вероятность того, что случайная величина принимает значения в интервале {х₁ х₂}, равна разности значений функции на концах интервала: P{xi<X<x₂} — F(x₂) - F(x₁).

Если x₂-x₁= ∆x то одинаковым приращениям ∆х соответствуют различные значения приращения вероятности ∆F(x). Тогда плотность распределения вероятностей случайной величины, или плотность вероятностей, будет иметь следующий вид:

 

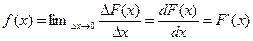(8.1)

Это дифференциальная форма представления F(x). В интегральной форме

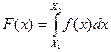(8.2)

Вероятность попадания случайной величины в интервал (х₁ х₂) будет равна интегралу от плотности распределения вероятности:

 

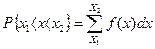(8.3)

Так как ∆=X-Q, то переход от законов распределения вероятностей результатов наблюдений к законам распределения вероятностей погрешностей сводится к замене х на ∆ в вышеприведенных формулах.

 

9 СЛУЧАЙНЫЕ ПОГРЕШНОСТИ ИЗМЕРЕНИЙ

9.1 Источники возникновения случайных погрешностей Случайными называются не определенные по своей величине и природе погрешности, в появлении которых не наблюдается какой-либо закономерности.

Случайные погрешности обнаруживаются при многократных измерениях искомой величины, так как результаты отдельных измерений отличаются друг от друга даже в тех случаях, когда повторные измерения проводятся одинаково тщательно и, казалось бы, при одних и тех же условиях. Другими словами, случайные погрешности неизбежны, и поэтому действительное значение Х_д находится с некоторым приближением. К случайным погрешностям можно отнести, например, погрешности отсчета за счет параллакса (в приборах, не снабженных зеркальной шкалой). В зависимости от расположения глаза наблюдателя конец стрелки кажется расположенным над той или иной точкой шкалы, т.е. фактически полученный отсчет зависит от расположения глаза (рисунок 9.1).

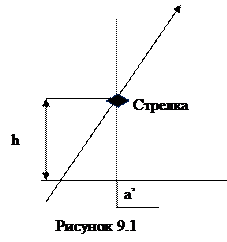
Правильным отсчетом надо считать точку шкалы, на которую проецируется стрелка при условии, что луч зрения (от зрачка к стрелке) перпендикулярен плоскости шкалы. Следовательно, отсчет производится в точке а', смещенной на некоторую величину по отношению к истинной точке а. В какую сторону и какой величины будет параллакс - зависит от случая. Но насколько в среднем велика погрешность - это зависит от конструкции прибора: чем меньше отношение расстояния h между стрелкой и шкалой к общей ширине шкалы, тем меньше будет в среднем погрешность. Следовательно, проектировщик обязан заранее учитывать ее и принимать конструктивные меры для уменьшения до допустимой величины.

К случайной относится также глазомерная погрешность, возникающая при определении на глаз доли деления. При конструировании обычно считают, что человек, имеющий необходимый навык, ошибается в отсчете на глаз не более чем на 1/10 деления. Это при условии, что шкала удовлетворяет определенным требованиям:

1)деления не слишком мелки - не менее 1,5 мм;

2)штрихи четкие, не размытые;

3)толщина штрихов и визирной черты или нити, толщина конца стрелки удобная; обычно рекомендуют толщину штриха около 0,15 мм;

4)цвет шкалы такой, чтобы штрихи четко выделялись;

5)в ночных условиях должно быть обеспечено достаточное освещение шкалы.

Погрешность (глазомерная или от параллакса), выраженная в процентах, будет тем меньше, чем крупнее шкала (т.е. чем меньше цена мелкого деления).

В качестве примера случайной погрешности можно также привести температурную погрешность, т.е. изменение показаний прибора в связи с тем, что окружающая температура отличается от нормальной, при которой была произведена градуировка шкалы. Для данного прибора можно заранее определить, на сколько изменяется показание при определенном повышении температуры. Следовательно, ее можно исключить путем учета поправки.

В большинстве случаев случайные погрешности нельзя исключить опытным путем, но их влияние на результат измерения может быть теоретически учтено применением при обработке результатов измерений теории вероятностей и математической статистики.

Нормальное распределение случайной погрешности (распределение Гаусса) подчиняется уравнению

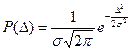(9.1)

где 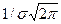- вероятность получения погрешностей (частота появления случайной погрешности ).

Функции распределения достаточно полно могут быть определены своими числовыми характеристиками, к которым относятся начальные и центральные моменты.

Начальным моментом к-порядка является математическое ожидание случайной величины степени к:

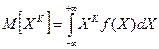. (9.2)

В большинстве случаев начальный момент 1-порядка совпадает с истинным значением измеряемой величины.

Центральный момент к-порядка - математическое ожидание к-й степени центрированной случайной величины (т.е. разности между значением случайной величины и ее математическим ожиданием). Применительно к измерениям центрированная случайная величина будет случайной погрешностью:

=X-M[X]=X-Q (9.3)

Центральным моментом 2-порядка будет дисперсия результатов наблюдений:

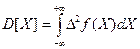. (9.4)

Это рассеяние результатов наблюдений относительно математического ожидания. Недостаток такого представления погрешности измерения заключается в том, что она имеет размерность квадрата измеряемой величины. Поэтому на практике используют значение среднеквадратичного отклонения результата измерения

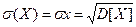. (9.5)

 

В отличие от результатов измерения, числовые характеристики функции распределения являются детерминированными, а не случайными. Следовательно, чтобы найти точные значения, необходимо произвести бесконечно большое число наблюдений. Отсюда возникает задача определения приближенных значений, полученных в некотором количестве независимых наблюдений. В математической статистике такие приближенные значения, выраженные одним числом, называются точечными оценками. Любая точечная оценка, вычисленная на основе опытных данных, представляет собой случайную величину, зависящую от самого оцениваемого параметра и от числа опытов. Распределение оценки зависит от распределения исходной случайной величины. Оценки классифицируются следующим образом:

· состоятельные, когда при увеличении числа наблюдений они приближаются к значению оцениваемого параметра;

· несмещенные, если математическое ожидание равно оцениваемому параметру;

· эффективные, если ее дисперсия меньше дисперсии любой другой оценки этого параметра.

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: