Главная | Обратная связь | Поможем написать вашу работу!

Методы Рунге-Кутта 2-го порядка.

Численное решение задачи Коши для дифференциальных уравнений 1 – го порядка.

Соотношение вида

, (1)

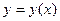где - некоторая функция независимой переменной , функции и ее производных , ,…, , называется обыкновенным дифференциальным уравнением n - го порядка.

Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение.

Решить уравнение, значит, найти n раз дифференцируемую функцию , превращающее соотношение (1) в тождество. Существует понятие общего и частного решения этого дифференциального уравнения.

Общим решением дифференциального уравнения называется n раз дифференцируемая функция , зависящая от n произвольных постоянных .

Решение дифференциального уравнения, полученное из общего решения при конкретных значениях произвольных постоянных , называется частным решением этого уравнения.

Для выделения частного решения из общего решения ДУ, кроме самого уравнения, необходимо иметь некоторые дополнительные условия, позволяющие определить значения произвольных постоянных . Одним из таких условий является задание искомой функции и ее производных до (n-1) порядка в некоторой точке , т.е. условий вида:

. (2)

Здесь - заданные числа. Эти дополнительные данные называют начальными условиями или условиями Коши. Наличие начальных условий позволяет получить частное решение дифференциального уравнения. Задача нахождения частного решения уравнения (1), удовлетворяющего начальным условиям (2), называется задачей Коши. Для ДУ n - го порядка имеет место теорема о существовании и единственности решения задачи Коши График каждого частного решения называется интегральной кривой.

Методы решения дифференциальных уравнений можно условно разбить на точные, приближенные и численные. Точные методы позволяют выразить решение ДУ через элементарные функции. Получить точное решение ДУ можно не всегда. Приближенные методы дают решение в виде некоторой последовательности функций , сходящейся к решению при . Примером может служить метод разложения решения в обобщенный степенной ряд. Численные методы дают значения искомого решения на некоторой выбранной сетке значений аргумента (узлов). Решение при этом получается в виде таблицы. Численные методы не позволяют найти общего решения уравнения (1),они могут дать только какое – то частное решение, например, решение задачи Коши.

Рассмотрим задачу Коши для обыкновенного дифференциального уравнения первого порядка:

, . (3)

Будем предполагать, что f(x,y) непрерывная и непрерывно дифференцируемая по функция в окрестности замкнутой области

содержащей внутри себя точку .

Будем решать задачу Коши численными методами.

Выберем на отрезке упорядоченную систему точек , называемую сеткой. Точки называют узлами, а - шагом сетки. Будем рассматривать равномерную сетку. Тогда узлы разбиения имеют вид .

Пусть − значения функции в узлах.

При численном решении задачи Коши для ОДУ первого порядка, используя начальные условия , мы последовательно находим по соответствующей рекуррентной формуле приближенное значение решения в узле , затем значение решения в узле и т д.

Рассмотрим некоторые из методов.

Метод рядов Тейлора.

Разложим точное решение y(x) в ряд Тейлора в окрестности точки , ограничившись 3 слагаемыми. Положим . Получим:

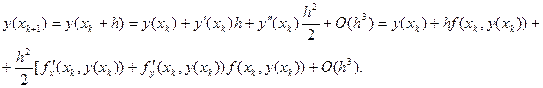(4)

Напомним, что при численном решении задачи Коши точное решение нам известно лишь в точке . Предположим, что мы нашли приближенное решение в точке . Воспользуемся формулой (4), чтобы получить приближенное решение в точке , для этого, вместо точного значения решения поставим приближенное .

Формула 2 – го порядка точности методом рядов Тейлора примет

вид:

. (5)

Метод рядов Тейлора, как и все последующие рассмотренные нами методы, является одношаговым. Для вычисления нового значения функции нам необходимо знать лишь одно предыдущее значение функции . К недостаткам метода относится получение производных и необходимость расчета значений трех функций , поэтому строятся другие формулы, имеющие ту же точность, но без указанных выше недостатков. Погрешность на отдельном шаге равна , на всем отрезке погрешность составит Метод имеет второй порядок точности

Можно построить формулы более высокого порядка точности, удерживая в разложении в ряд Тейлора большое число слагаемых.

Метод Эйлера.

Формулу Эйлера можно получить, удерживая в формуле рядов Тейлора лишь два слагаемых. Формула имеет вид:

Погрешность на отдельном шаге равна , на всем отрезке погрешность составит . Метод имеет первый порядок точности.

Метод Эйлера иногда называют методом ломанных из-за его геометрического смысла. В точке проводится касательная к интегральной кривой y(x). Новое значение функции определяется как точка пересечения касательной с вертикальной прямой . Вообще говоря, мы попадаем на новую интегральную кривую уравнения (2). Следующая касательная к новой интегральной кривой проводится в точке .