Метод Рунге-Кутта 4-го порядка.

Расчеты осуществляются по формулам:

В данном методе погрешность на отдельном шаге , на всем отрезке погрешность составляет .

Оценка погрешности методов по правилу Рунге.

Для практической оценки погрешности используется правило Рунге. В узле вычисляется приближенное решение с шагом h и h/2. Разность между точным решением и приближенным решением (значение решения в узле с шагом h/2) оцениваетсявыражением:

,

где - значение решения в узле, вычисленное с шагом h, p – порядок метода.

 

Рассмотрим данные методы на примере. Будем решать задачу Коши для дифференциального уравнения

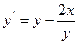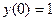, . (6)

Найдем решение уравнения (6) на отрезке [0,1] численными методами.

Разобьем отрезок интегрирования на 5 равных частей:

.

 

Получили 6 узлов, в них будем искать значения решения нашего уравнения.

Точное решение уравнения имеет вид:

 

Значения точного решения в узлах сетки равны:

 

Еще раз напомним, что при численном решении задачи Коши, решение получаем в виде таблицы значений решения в узлах.

Решим уравнение методом Эйлера.

Найдем значение решения в узле , для этого подставим в формулу для расчетов начальные условия. Получим:

.

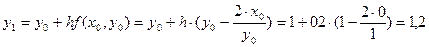Значение решения в узле :

и на всей сетке узлов соответственно:

 

Найдем решение уравнения методом Эйлера – Коши.

В узле , с шагом :

Соответственно значения решения на сетке узлов равны:

 

 

 

Теперь сгустим сетку, уменьшим шаг интегрирования вдвое: . Аналогично вычислим значения решения методом Эйлера – Коши на новой сетке. Получим:

 

 

 

Как видим, теперь значение решения в узле x=0,2 мы получили через значение решения в узле x=0,1. Оценим абсолютные погрешности решений (точное решение нам известно) с шагом и 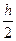на первоначальной сетке узлов. В узле x=0,2,с шагом и 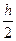соответственно:

 

Оценим также погрешность решения с шагом 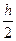в узле x=0,2 по правилу Рунге:

.

Произведем расчеты для метода Эйлера – Коши по всей сетке узлов, данные сведем в таблицу.

 

	0,2	1,18322	1,18667	0,00345	1,1841	0,00088	0,00086
	0,4	1,34164	1,34831	0,00667	1,34336	0,00172	0,00165
	0,6	1,48324	1,4937	0,01046	1,48526	0,00272	0,00258
	0,8	1,61245	1,62786	0,01541	1,61647	0,00402	0,0038
		1,73205	1,7542	0,02215	1,73787	0,00582	0,00545

 

Как видно из таблицы, с уменьшением шага интегрирования, погрешность нахождения решения уменьшается, вместе с тем, с ростом x (к концу отрезка) погрешность может накапливаться. Последние две колонки характеризуют реальную и ожидаемую погрешность решения с шагом .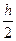

Решим наше уравнение методом Рунге-Кутта 4-го порядка.

Программно организуем процесс в системе MathCAD.

 

 

 

 

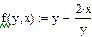
Получим:

 

 

Задание:

1. Решить задачу Коши для ОДУ 1 –го порядка методом Рунге – Кутта 4-го порядка с точностью . Шаг интегрирования , обеспечивающий требуемую точность, выбирать в процессе вычисления из сравнения результатов, полученных с и (правило Рунге). В случае необходимости шаг должен быть уменьшен. Количество узлов – 6.

2. Решить ОДУ методом в соответствии с вариантом.

3. Методы оформить в виде отдельных подпрограмм.

4. Вывод на консоль: i, узел, значения решения каждым из методов, точное значение, реальная и ожидаемая погрешность (по правилу Рунге).

5. Проанализировать полученные результаты и сделать выводы.

Варианты методов

0. Метод рядов Тейлора.

1. Метод Эйлера.

2. Модифицированный метод Эйлера.

3. Метод Эйлера – Коши.

 

Вариант метода соответствует остатку от деления номера по списку на 4.

 

Варианты ОДУ.

 

№ вар.	ОДУ	Начальные условия	Отрезок интегрирования	Точное решение уравнения

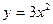
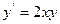
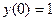
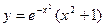
⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: