Гармонические функции. Основы метода комплексных амплитуд

Министерство образования и науки Российской Федерации

Марийский Государственный Технический Университет

 

 

Кафедра РТ и МБС

 

Расчетно-графическая работа

По дисциплине

«Основы теории цепей».

 

ЛИНЕЙНЫЕ ЦЕПИ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ.

 

 

Выполнил: ст.гр.РТ-21

 

 

Проверил: к.т.н., доцент

Калачев Е.Н.

 

 

Йошкар-Ола

Введение.

Если значения функции времени a(t) изменяются по синусоидальному или косинусоидальному закону a(t)=A_mcos(w t+y)=A_msin(w t+y¢), где y¢=y+p/2, то такая функция называется гармонической. Наибольшее значение гармонической функции A_m называется амплитудой. Аргумент q=w t+y функции называется мгновенной фазой (фазой). Величина y называется начальной фазой. Скорость изменения фазы w=dq/dt называется угловой частотой. Гармоническая функция времени называется периодической, если ее значения повторяются через определенные промежутки времени. Наименьшее промежуток времени T, через который наблюдается повторение значений функции, называется периодом. Величина, обратная периоду, называется частотой: f= 1/ T(1).

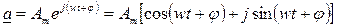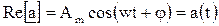Гармонической функцией времени а(t) можно поставить в соответствие число а, называемое мгновенным или текущим комплексом гармонической функции: , модуль которого равен амплитуде гармонической функции А_m, а аргумент ее мгновенной фазе . Вещественная часть мгновенного комплекса а равна исходной гармонической функции: . Значение мгновенного комплекса а в момент времени t=0 называется комплексной амплитудой A_m: . Комплексное действующее значение гармонической функции а(t) можно определить из выражения:

Представление токов и напряжений в виде гармонических или других периодических функций времени следует рассматривать как приближенное математическое описание реальных процессов, имеющих место в электрической цепи.

Комплексным числом А называется выражение вида: А=А¢+jА¢¢(1), где А¢, А¢¢ - действительные числа, называется вещественной и мнимой составляющими комплексного числа; j= - мнимая единица. Выражение (1) называется алгебраической формой записи комплексного числа.

Тригонометрическаяформа записи комплексного числа: А=½А½ cosa+j ½А½ sina. Используя, формулу Эйлера: е^ja= cosa+jsina. Получаем показательную форму записи комплексного числа А=½А½ е^ja.

Первый закон Кирхгофа (уравнение баланса токов в узле): сумма мгновенных значений токов, направленных к любому узлу цепи, в любой момент времени равна сумме токов, направленных от этого узла.

Второй закон Кирхгофа (уравнение баланса напряжений ветвей): алгебраическая сумма мгновенных значений напряжений на всех элементах любого контура моделирующей цепи, за исключением источников напряжения в каждый момент времени, равна алгебраической сумме мгновенных значений ЭДС источников напряжения, действующих в этом контуре.

Уравнения баланса токов и напряжений можно применять для математического описания процессов в моделирующих цепях, составленных из двухполюсных элементов любого типа (как линейных, так и нелинейных) при любой форме токов и напряжений независимых источников.

Производная энергии по времени представляет собой мгновенную мощность: p=¶ w/¶ t. Активная мощность численно равна постоянной составляющей мгновенной мощности и характеризует среднюю за период скорость потребления энергии от источника. Полной мощностью называется величина, равная произведению действующих значений тока и напряжения на зажимах цепи. Комплексное число, модуль которого равен полной мощности цепи, а аргумент – углу сдвига фаз между током и напряжения, называется комплексной мощностью цепи. Реактивная мощность характеризует процессы обмена энергией между цепью и источником, она численно равна максимальной скорости запасания энергии в цепи. Уравнение баланса мгновенных мощностей: сумма мгновенных мощностей, отдаваемых всеми источниками, равна сумме мгновенных мощностей, потребляемых всеми приемниками.

 

Гармонические функции. Основы метода комплексных амплитуд

 

1.1. Найдем амплитуды, действующие значения, частоты, угловые частоты, периоды и начальные фазы гармонических токов и напряжений.

 

i₁(t)=100sin628t A

I_m=100 (A), w=628 рад/с

I=0.707*100=70.7 (A)

ƒ=628/2π=100 (Гц)

T=1/100=0.01 (с)

φ= φ'- π/2

φ= - π/2

i₂(t)=200cos(1000t-15°) A

I_m=200 (A), w=1000 рад/с

I=0.707*200=141.4 (A)

ƒ=1000/2π=159 (Гц)

T=1/159=0.0063 (с)

φ=-15°

u₁(t)=0.15sin(10t+90°) мB

U_m=0.15 (мВ), w=10 рад/с

U=0.707*0.15=0.106 (мB)

ƒ=10/2π=1.6 (Гц)

T=1/1.6=0.625 (с)

φ= φ'- π/2

φ= 0°

 

u₂(t)=14cos(300t+π/4) B

U_m=14 (A), w=300 рад/с

U=0.707*14=9.9 (B)

ƒ=300/2π=47.7 (Гц)

T=1/47.7=0.021 (с)

φ= 45°

 

 

1.2. Определим мгновенные комплексы, комплексные амплитуды, комплексные действующие значения для заданных в пункте 1.1 гармонических токов и напряжений.

 

i ₁=100e^j(628t-π/2) А=100[cos(628t-π/2)+jsin(628t-π/2)] А

i ₂=200e^{j(1000t-15°)} А=200[cos(1000t-15°)+jsin(1000t-15°)] А

u ₁=0.15e^j10t мВ=0.15[cos10t+jsin10t] мВ

u ₂=14e^j(300t+45°) В=14[cos(300t+45°)+jsin(300t+45°)] В

İ_m1=100e^-jπ/2 А İ₁=70.7e^-jπ/2 А

İ_m2=200e^-j15 А İ₂=141.4e^-j15 А

Ů_m1=0.15 мВ Ů₁=0.106 мВ

Ů_m2=14e^j45 В Ů₂=9.9e^j45 В

1.3. Перейдем от алгебраической формы записи комплексных действующих значений токов и напряжений к показательной форме записи их комплексных амплитуд.

I₁=0.1+j0.3 A

׀ İ₁ ׀ =0.32 (А)

tgφ=3 Þ φ=arctg3=71.6°

İ₁=0.32e^71.6j А

I₂=-10+j25 мк A

׀ İ₂ ׀ =26.9 (мкА)

tgφ=2.5 Þ φ=90°+arctg2.5=152.8°

İ₂=26.9e^152.8j мкА

U₁=-8-j6 мB

׀ Ů₁ ׀ =10 (мВ)

tgφ=0.75 Þ φ=180°+arctg0.75=216.9°

Ů₁=10e^-143.1j мВ

U₂=j3 B

׀ Ů₂ ׀ =3 (В)

tgφ=∞ Þ φ=arctg∞=90°

Ů₂=3e^90j В

 

1.4. Запишем выражения для мгновенных значений токов и напряжений, соответствующих выражениям комплексных амплитуд токов и напряжений, полученным в пункте 1.3. Частота токов и напряжений одинакова и равна 1000 Гц.

 

i(t)=A_mcos(2πƒt+φ) A

i₁(t)=1.41*0.32cos(2π*1000t+71.6°) A=0.45cos(6280t+71.6°) А

i₂(t)=1.41*26.9cos(2π*1000t-68.2°) A=37.9cos(6280t-68.2°) А

u₁(t)=1.41*10cos(2π*1000t+36.9°) мВ=14.1cos(6280t+36.9°) мВ

u₂(t)=1.41*3cos(2π*1000t+90°) В=4.23cos(6280t+90°) В

 

1.5. Построим временные диаграммы мгновенных токов и напряжений, определённых в пункте 1.4.

 

Для тока i₁(t)= 0.45cos(6280t+71.6°) А временная диаграмма представлена на рисунке 1.1.

 

 

Рис. 1.1.

 

Для тока i₂(t)= 37.9cos(6280t-68.2°) А временная диаграмма представлена на рисунке 1.2.

 

 

Рис. 1.2.

 

 

Для напряжения u₁(t)=14.1cos(6280t+36.9°) мВ временная диаграмма представлена на рисунке 1.3

 

Рис. 1.3.

 

Для напряжения u₂(t)=4.23cos(6280t+90°) В временная диаграмма представлена на рисунке 1.4.

 

Рис. 1.4.

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: