 |
Анализ электрических цепей методом комплексных амплитуд.
|
|
|
|
 |
Рис. 2.1.
E1=20sin(103t+60°)=20cos(103t-30°) B; L1=20 мГн; C1=10000 пФ;
E2=50cos(103t+45°) B; L2=300 мГн; С2=400 пФ;
R1=5 Oм; L3=50 мГн;
R2=100 Oм; L4=300 мГн;
R3=200 Oм; L5=10 мГн;
R4=10 Oм.
Рассчитаем мгновенные значения токов и напряжений схемы (рис. 2.1). Для начала заменим схему цепи (рис. 2.1) комплексной схемой замещения (рис 2.2). Будем считать, что токи и напряжения ветви направлены одинваково.
Число ветвей р=5, число узлов q=3, следовательно, основная система уравнений электрического равновесия содержит 2р=10 уравнений.
Составим систему уравнений.
На основании первого закона Кирхгофа составляем m=q-1=2 уравнений баланса токов:
(1) 
- 
- 
=0;
(2) - 
- 
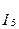=0;
На основании второго закона Кирхгофа составляем n=р-q+1=3 уравнений баланса напряжений.
(3) 
;
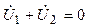(4) 
;
(5) 
.
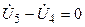Запишем компонентные уравнения, связывающие токи и напряжения ветвей:
= 
- 
;
= 
;
= 
;
= 
;
=- 
- 
;
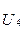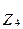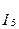
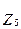Запишем Е1 и Е2 в комплексной форме.
=17.6-j9.6 B;
=34.8+j35.9 B.
Найдем комплексное сопротивление ветвей.
=R1+jwL1=5+j103*20*10-3=5+j20 Ом;
= R2+jwL2=100+j103*300*10-3=100+j300 Ом;
= R3+j[wL3-1/(wC1)]=200+j[103*50*10-3-1/(103*10000*10-12)]=200-j99950 Ом;
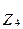= j[wL4-1/(wC2)]=j[103*300*10-3-1/(103*400*10-12)]=-j2499700 Ом;
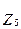=R4+jwL5=10+j103*10*10-3=10+10j Ом.
Подставляя компонентные уравнения в уравнения баланса напряжений, получаем в сочетании с уравнениями баланса токов сокращенную систему уравнений.
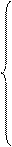
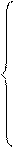
- + =0; - = ;
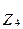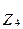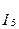
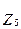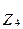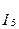
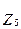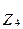+ - =0; + - =0;
- - - =0; - - = ;
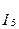- - =0; - - =0;
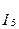- - =0; - - =0;
Все расчеты выполнены MathCAD 2001 Rus.
=0.011+j0.067, A; = -18.884+j10.157, B;
=0.012+j0.067, A; =-18.884+j10.157, B;
=-0.00046+j0.00016, A; = 15.91+j46.054, B;
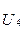=0.000014-j0.000014, A; = -34.794-j35.897, B;
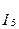=-0.00047+j0.00017, A. = -34.794-j35.897, B.
Переведем из комплексной формы в гармоническую функцию полученные токи и напряжения.
=0.011+j0.067, A;
y=arctg(0.067/0.011)= 80.7°;
|
|
|
=68ej80.7°j мA;
=68cos(103t+80.7°)+68jsin(103t+80.7°), мA;
i1=Re[ ]= 68cos(103t+79.8°), мA.
=0.012+j0.067, A;
y=arctg(0.067/0.012)= 79.8°;
=68ej79.8° мA;
=68cos(103t+79.8°)+68jsin(103t+79.8°), мA;
i2=Re[ ]= 68cos(103t+79.8°), мA.
=-0.00046+j0.00016, A;
y= p/2+arctg(0.00016/0.00046)= 109.2°;
=490ej109.2° мкA;
=490cos(103t+109.2°)+490jsin(103t+109.2°), мкA;
i3=Re[ ]= 490cos(103t+109.2°), мкA.
=0.000014-j0.000014, A;
y= -arctg(0.000014/0.000014)= -45°;
=20e-j45° мкA;
=20cos(103t-45°)+20jsin(103t-45°), мкA;
i4=Re[ ]= 20cos(103t-45°), мкA.
I5=-0.00047+j0.00017, A.
y= p/2+arctg(0.00017/0.00047)= 109.9°;
I5=500ej109.9° мкA;
I5=500cos(103t+109.9°)+500jsin(103t+109.9°), мкA;
i5=Re[I5]= 500cos(103t+109.9°), мкA.
= -18.884+j10.157, B;
y=p/2+arctg(10.157/18,884)= 118.3°;
=21.4ej118.3° B;
=21.4cos(103t+118.3°)+21.4jsin(103t+118.3°), B;
u1=Re[ ]= 21.4cos(103t+118.3°), B.
=-18.884+j10.157;
y=p/2+arctg(10.157/18.884)= 118.3°;
=21.4ej118.3° B;
=21.4cos(103t+118.3°)+21.4jsin(103t+118.3°), B;
u2=Re[ ]= 21.4cos(103t+118.3°), B.
= 15.91+j46.054, B;
y= arctg(46.054/15.91)= 70.9°;
=48.7ej70.9° B;
=48.7cos(103t+70.9°)+48.7jsin(103t+70.9°), B;
u3=Re[ ]= 48.7cos(103t+70.9°), B.
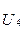= -34.794-j35.897, B;
y= p+arctg(-35.897/-34.794)= 225.9°;
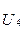=50ej225.9° B;
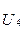=50cos(103t+225.9°)+50jsin(103t+225.9°), B;
u4=Re[ 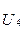]= 50cos(103t+225.9°), B.
= -34.794-j35.897, B.
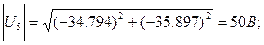
y= p+arctg(-35.897/-34.794)= 225.9°;
=50ej225.9° B;
=50cos(103t+225.9°)+50jsin(103t+225.9°), B;
u5=Re[ ]= 50cos(103t+225.9°), B.
Полученные результаты:
i1= 68cos(103t+79.8°), мA. u1= 21.4cos(103t+118.3°), B.
i2= 68cos(103t+79.8°), мA. u2= 21.4cos(103t+118.3°), B.
i3= 490cos(103t+109.2°), мкA. u3= 48.7cos(103t+70.9°), B.
i4= 20cos(103t-45°), мкA. u4= 50cos(103t+225.9°), B.
i5= 500cos(103t+109.9°), мкA. u5= 50cos(103t+225.9°), B.
3. Идеализированные пассивные элементы при
гармоническом воздействии.
u(t)=6cos1000t, B i(t)=0.6cos(1000t-45°), mA.
1. j=ju-jI=0-(-45°)=45°.
Так как реактивная мощность цепи положительная(0< j< p/2), то сопротивление имеет резистивно-индуктивный характер.
;
;
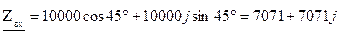а) последовательное соединение.
z =R+jwL;
7071=L*1000*6.28 Þ 
R=7.07 Ом
б) параллельное соединение.
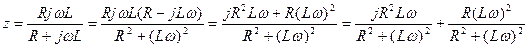
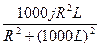=7071j;
=7071;
Все расчеты выполнены Mathcad 2000 Professional.
L=14.1 Гн;
R=14100 Ом.
2. Найдем:
a) мгновенную мощность.
p=ui=6cos1000t*0,0006cos(1000t-45°)=0,0018[cos(2000t-45°)+cos45°]= =0.0018cos(2000t-45°)+0.0013, Bт.
b) полную мощность.
PS=ImUm=6*0.0006=0.0036 В×A.
c) активную мощность.
j=ju-jI=0-(-45°)=45°.
PA= PScosj=0.0036cos45°=0.0025 Вт
d) реактивную мощность.
PQ= PSsinj=0.004sin45°=0.0025 вар.
e) Комплексную мощность.
|
|
|
PS =PSejj=0.0036ej45° В×A.
4. Простейшие линейные цепи при гармонических воздействиях.
u=4cos(106+60°) B;
R=4 Oм;
L=0.2 мГн;
С=0.1 мкФ
a) параллельная RL-цепь
 |
Рис.4.1.а.
Найдем комплексное входное сопротивление цепи.
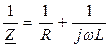Þ 
; 
Ом
Рис.4.2.а.
Найдем комплексные действующие значения токов и напряжений на элементах цепи. Для определения комплексных действующих значений токов и напряжений на элементах цепи запишем комплексное действующее напряжение, приложенное к зажимам цепи в показательной форме:
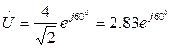В
Аналогично запишем комплексное входное сопротивление цепи:
Ом
На основании закона Ома:
А
Так, как соединение параллельное, то: 
.
А
А
Рис.4.3.а.
б) последовательная RC-цепь.
 |
Рис.4.1.б.
Найдем комплексное входное сопротивление цепи.
Ом.
Рис.4.2.б.
Запишем комплексное действующее значение напряжения и комплексное входное сопротивление в показательной форме:
Ом
Ом
На основании закона Ома: 
А
Найдем комплексные действующие значения токов и напряжений на элементах цепи. Так как цепь последовательная, то: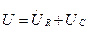 
А.
В
В
Рис.4.3.б.
в) параллельная RLC-цепь
Рис 4.1.в.
Ом-1
Ом
Запишем комплексное действующее значение напряжения и комплексное входное сопротивление в показательной форме:
Ом
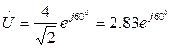В
На основании закона Ома: 
А
Рис.4.2.в.
Найдем комплексные действующие значения токов и напряжений на элементах цепи. Так как цепь параллельная, то
В 
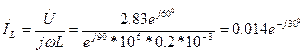А
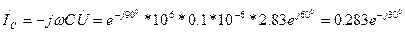А
А
Рис.4.3.в.
5. Преобразование электрических цепей
5.1 Используя эквивалентные преобразования участков цепей определим комплексное входное сопротивление цепи, изображенной на рисунке 5.1. Параметры элементов цепи и частота гармонического воздействия указаны в таблице 5.1.
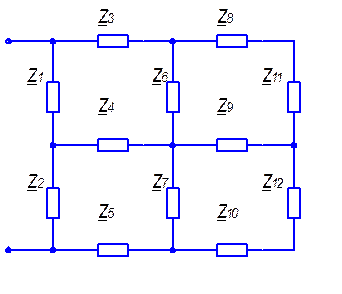
Рис. 5.1.
Таблица 5.1.
| Частота, кГц | Параметры элементов | ||||||
| Z 1= Z 2 | Z 3 | Z 4 | Z 5= Z 6 | Z 7= Z 8 | Z 9= Z 10 | Z 11= Z 12 | |
| R=50кОм | R=50кОм | L=50мГн | R=50кОм | R=50кОм | R=500Ом | R=2кОм |
Определим комплексные сопротивления Z 1… Z 12:
Z 1= Z 2= R= 50кОм
Z 3= R=50 кОм
Z 4=j2πfL=j*2π*50*10-3*3*103=j300π=j0.942 кОм
Z 5= Z 6= R=50 кОм
Z 7= Z 8= R=50 кОм
Z 9= Z 10= R=0.5 кОм
Z 11= Z 12= R=2кОм
Преобразуем схему. Так как Z8 и Z11, Z10 и Z12 соединены последовательно, то схема примет вид (рис. 5.2.):
|
|
|
Рис. 5.2.
кОм
кОм
Применим преобразование звезда-треугольник к группам сопротивлений Z 1, Z 4, Z 2; Z 8,11, Z 6, Z 3; Z 5, Z 7, Z 10,12. Полученная схема примет вид (рис. 5.3.):
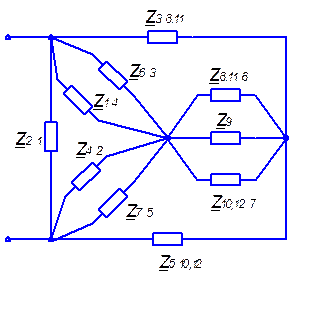
Рис. 5.3.
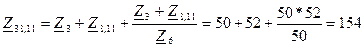кОм
кОм
кОм
кОм
кОм
кОм
кОм
кОм
кОм
Так как сопротивления Z 6 3 и Z 1 4, Z 8,11 6 и Z 9 и Z 10,12, Z 42 и Z 75 соединены параллельно, то схема примет вид (рис. 5.4.):
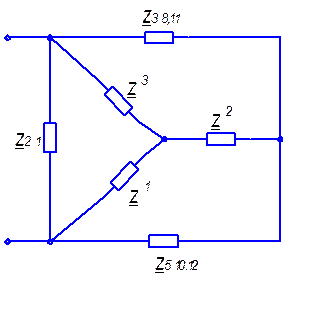
Рис. 5.4.
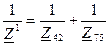
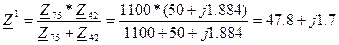кОм
кОм
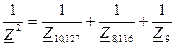
кОм
Применим преобразование звезда-треугольник к сопротивлениям Z 1, Z 2, Z 3. полученная схема примет вид (рис. 5.5.):
Рис. 5.5.
кОм
кОм
кОм
Сопротивления Z 38,11 и Z 23, Z 12 и Z 510,12, Z 21 и Z 31 соединены параллельно, поэтому схема (рис. 5.5.) примет следующий вид (рис. 5.6.):
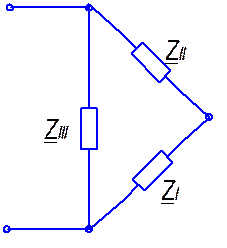
Рис. 5.6.
кОм
кОм
кОм
Сопротивления Z I и Z II соединены последовательно, поэтому схема (рис. 5.6.) преобразуется в эквивалентную схему (рис. 5.7.):
Рис. 5.7.
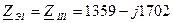кОм
кОм
Преобразую схему (рис. 5.7.), получаем схему (рис. 5.8.) с одним эквивалентным сопротивлением:
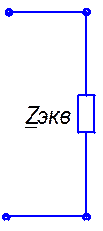
Рис. 5.8.
Так как сопротивления Z ЭI и Z ЭII соединены параллельно, то Zэкв будет равно:
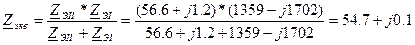кОм
5.2 Определим входное сопротивление цепи, схема которой изображена на рис. 5.9. Величины параметров элементов цепи приведены в таблице 5.2.
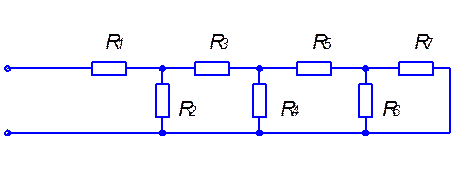
Рис. 5.9.
Таблица 5.2.
| Величины параметров элементов | ||||||
| R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом | R7, Ом |
Запишем сопротивление цепи (рис. 5.9.) в виде непрерывной дроби:
Ом
Вывод:
§ каждой гармонической функции времени можно единственным образом поставить в соответствие комплексное число (комплексную амплитуду), которое можно рассматривать как изображение этой гармонической функции на плоскости;
§ линейным операциям над гармоническими функциями времени соответствуют операции над их комплексными амплитудами, причем операции дифференцирования и интегрирования заменяются операциями умножения и деления. Эти свойства комплексных изображений гармонических функций позволяют существенно упростить анализ линейных цепей;
§ комплексная схема замещения цепи может быть получена из схемы замещения для мгновенных значений всех идеализированных пассивных двухполюсников их комплексными сопротивлениями (проводимостями) и всех токов и напряжений – их комплексными изображениями;
|
|
|
§ законы Кирхгофа были сформулированы только для мгновенных значений комплексных амплитуд и комплексных действующих значений токов и напряжений;
§ методы формирования уравнений электрического равновесия цепи, основанные на непосредственном применении законов Кирхгофа, позволяют уменьшит число одновременно решаемых уравнений;
§ комплексные сопротивления и проводимости идеализированных пассивных элементов линейных цепей не зависит от амплитуды (действующего значения) и начальной фазы внешнего воздействия и определяются только параметрами элементов и частотой внешнего воздействия;
§ уравнения, описывающие процессы в параллельной RLC-цепи, подобны по структуре уравнениям электрического равновесия последовательной RLC-цепи и могут быть получены одно из другого путем замены тока на напряжение, проводимости на сопротивление, емкости на индуктивность. Следовательно, параллельная и последовательная RLC-цепи являются дуальными. Векторные диаграммы дуальных цепей также могут быть получены одни из других путем упомянутых замен.
§
|
|
|
