 |
Прогноз на основе построения регрессионных моделей
|
|
|
|
По данным Министерства труда, занятости и социальной защиты РТ, а так же по материалу Территориального органа Федеральной службы государственной статистики по Республике Татарстан для прогнозирования на основе построения регрессионных моделей были взяты данные о просроченной задолженности по заработной плате республики Татарстан в разрезе муниципальных образований. (Раздел II Трудовые отношения – «Информационно статистический бюллетень №3»).
Просроченная задолженность по заработной плате в Республике Татарстан в разрезе МО Таблица 5
| Наименование муниципального образования | Численность работников, перед которыми организации имеют просроченную задолженность по з/п, чел. Х | Сумма задолженности по з/п, тыс. руб. Y |
| Бавлы | ||
| Бугульма | ||
| Бугульминский район | ||
| Буинск | ||
| Высокогорский район | ||
| Елабужский район | ||
| Зеленодольск | ||
| Зеленодольский район | ||
| Лаишевский район | ||
| Лениногорск | ||
| Лениногорский район | ||
| Hижнекамский район | ||
| Нурлат | ||
| Набережные Челны | ||
| Сабинский район | ||
| Тетюшский район | ||
| Тюлячинский район | ||
| Чистопольский район | ||
| Казань | ||
| Авиастроительный | ||
| Вахитовский | ||
| Кировский | ||
| Московский | ||
| Hово-Савиновский | ||
| Приволжский | ||
| Советский |
Выполним регрессионный анализ. Результаты регрессионного анализа размещаются в четырех таблицах: регрессионной статистики, дисперсионного анализа, параметров модели, прогнозных значений и остатков.
Регрессионная статистика
Таблица 6
|
|
|
| Регрессионная статистика | |
| Множественный R | 0,952091373 |
| R-квадрат | 0,906477983 |
| Нормированный R-квадрат | 0,902581233 |
| Стандартная ошибка | 1889,676923 |
| Наблюдения |
Таблица регрессионной статистики оценивает корреляционную связь. Множественный R – коэффициент корреляции. Коэффициент корреляции больше 0,95209 – связь весьма высокая по шкале Чеддока (таблица 7).
Шкала Чеддока
Таблица 7
| Коэффициент детерминации | 0,1-0,3 | 0,3-0,5 | 0,5-0,7 | 0,7-0,9 | 0,9-0,99 |
| Характеристика силы связи | слабая | умеренная | заметная | высокая | весьма высокая |
R-квадрат – коэффициент детерминации, он характеризует тесноту связи результативного и факторного признаков. Качественная оценка степени связи случайных переменных может быть выявлена на основе оценки коэффициента детерминации по шкале Чеддока (таблица 7). Теснота связи равна 0,906477, по шкале Чеддока связь весьма высокая.
Стандартная ошибка – среднеквадратическое значение отклонения регрессии от эмпирических данных.
Наблюдения – количество (n) наблюдений в массиве. Показателю соответствует 26 наименований задолженников Муниципальных образований Республики Татарстан.
Оценим статистическую надежность регрессионного уравнения и коэффициента множественной детерминации с помощью F-критерия Фишера, используя таблицу дисперсионного анализа.
Таблица дисперсионного анализа ANOVA
Таблица 8
| Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 830672356,03 | 232,6241 | 7,54904E-14 | ||
| Остаток | 85701092,93 | 3570878,872 | |||
| Итого | 916373448,96 |
df – число степеней свободы; для строки Регрессия это m число переменных (рассматриваемых факторов) в уравнении регрессии, для строки Остаток – размер выборки минус число параметров в регрессии минус 1 (n-m-1), для строки Итого – размер выборки минус 1 (n-1).
SS – сумма квадратов отклонений для расчета дисперсии: для строки Регрессия – факторной, для строки Остаток – остаточной, для строки Итого – общей.
|
|
|
MS – дисперсия, рассчитываемая как отношение суммы квадратов отклонений к величине df.
F – статистика (F-критерий Фишера) для оценки связи между зависимой и независимыми переменными. Если Fрасчетное>Fтабличное при заданном уровне значимости α и k1=m, k2=n-m-1 (m – число независимых факторов, n – число наблюдений), то уравнение линейной регрессии и коэффициент корреляции статистически значимы.
Значимость F – значение уровня значимости α, соответствующее вычисленному значению F. Вероятность правильного прогноза 1-α..
F Фишера:
Fрас =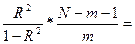 
232,62
Fтаб =(0,05; 1;26-1-1)= 4,26
Fрас > Fтаб, уравнение линейной регрессии и коэффициент корреляции статистически значимы.
По таблице параметров модели и их статистических оценок определим коэффициенты регрессии и оценим значимость коэффициентов регрессии с помощью t-статистик Стьюдента при уровне значимости α=0,05 и d.f.=n-m-1
Таблица параметров модели и их статистических оценок
Таблица 9
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y-пересечение | 108,76 | 434,25 | 0,25 | 0,80 | -787,48 | 1005,01 | -787,48 | 1005,01 |
| Численность работников, перед которыми организации имеют просроченную задолженность по з/п, чел. Х | 13,83 | 0,91 | 15,25 | 0,00 | 11,96 | 15,70 | 11,96 | 15,70 |
Коэффициенты – значения параметров модели регрессии.
Стандартная ошибка – параметров уравнения регрессии.
t- статистика – отношение Коэффициент/Стандартная ошибка (t-критерий Стьюдента). Если t расчетное > t табличное при заданном уровне значимости и P-значение меньше принятого уровня значимости, то коэффициенты регрессии статистически значимы.
P-значение – уровень значимости α для значений t-статистики.
t Стьюд. табл=СТЬЮДРАСПОБР(0,05;24)= 2,063898547
t рас > t таб, коэффициент корреляции статистически значим.
Верхние и Нижние – границы доверительного интервала для коэффициентов уравнения регрессии. Если в доверительный интервал не попадает ноль, то коэффициенты регрессии статистически значимы.
Таблица прогнозных значений по модели остатков
Таблица 10
| Наблюдение | Предсказанное Сумма задолженности по з/п, тыс. руб. Y | Остатки | Стандартные остатки |
| 537,4300155 | -311,4300155 | -0,168204377 | |
| 3081,770351 | 1339,229649 | 0,723322342 | |
| 2736,071936 | -1318,071936 | -0,711894991 | |
| 1284,138592 | -622,1385922 | -0,336019102 | |
| 3289,1894 | 3549,8106 | 1,91726439 | |
| 592,741762 | -377,741762 | -0,204019569 | |
| 5888,841481 | -972,8414814 | -0,525434886 | |
| 2514,82495 | -928,82495 | -0,501661413 | |
| 2570,136696 | -1144,136696 | -0,617951996 | |
| 2736,071936 | -1236,071936 | -0,667606521 | |
| 357,6668397 | -162,6668397 | -0,087856896 | |
| 205,559537 | 66,44046296 | 0,035884713 | |
| 219,3874736 | -66,38747365 | -0,035856093 | |
| 1242,654782 | -542,6547824 | -0,293089634 | |
| 454,4623959 | 4445,537604 | 2,401049493 | |
| 938,4401771 | -788,4401771 | -0,425839135 | |
| 1989,363359 | -1234,363359 | -0,666683713 | |
| 6842,969107 | -3485,969107 | -1,882783389 | |
| 29175,08672 | 271,9132768 | 0,146861256 | |
| 6303,67958 | 4531,32042 | 2,447381075 | |
| 3441,296702 | -1990,296702 | -1,0749658 | |
| 2597,79257 | 1807,20743 | 0,976078682 | |
| 744,8490646 | 832,1509354 | 0,449447459 | |
| 482,1182691 | -220,1182691 | -0,118886602 | |
| 2003,191296 | -1103,191296 | -0,59583725 | |
| 10355,265 | -338,2650046 | -0,182698042 |
|
|
|
Предсказанное Y – расчетные значения по модели регрессии.
Остатки – разность эмпирического и предсказанного по модели регрессии значений.
Рассчитаем средний частный коэффициент эластичности Эxi:
Эxi = 0,96945657
По таблице прогнозных значений по модели и остатков рассчитайте среднюю ошибку аппроксимации A по формуле:
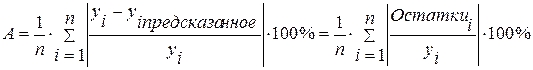
Используем функцию ABS для определения модулей выражений и функцию СУММ для суммирования.
А = 0,93066
Определим прогнозное значение среднедушевого прожиточного минимума Xпрогн., используя статистическую функцию СРЗНАЧ. Определим прогнозное значение среднедневной зарплаты Yпрогн. по формулам:
Х прогноз = 267,1296154
У прогноз = 3802,615367
По таблице дисперсионного анализа ANOVA определим остаточную дисперсию и с помощью математической функции КОРЕНЬ рассчитаем среднюю стандартную ошибку прогноза my и предельную ошибку Δ по формулам:
где σ ост – квадратный корень из остаточной дисперсии.
где tтабл. – табличное значение t-критерия Стьюдента при заданном уровне значимости α=0,05.
My = 1925,674003
∆ = 8202,749673
Доверительный интервал прогноза рассчитываем по формуле:
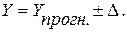
-4400,134306≤Y≤ 12005,36504
Список использованных источников
1. Информационно-статистический бюллетень №3.Труд, занятость, социальная защита в Республике Татарстан. – Казань, 2010г.
|
|
|
2. Особенности рынка труда. Стратегия и управление.ru/http://www.strategplann.ru/ett/osobennosti-rynka-truda.html
3. Республика Татарстан: путеводитель инвестора. При поддержке Министерства экономики РТ.-Казань2010.-15-16с.
4. Рынок труда. Учебник. Под ред. Проф. В.С.Буланова и проф. Н.А,Волгина. – М.: «Экзамен», 2000. – 448 с.
5. Ситуация на рынке труда в Татарстане. Безформата.ru/ http://kazan.bezformata.ru/listnews/situatciya-na-rinke-truda-v-tatarstane/939710/
6. Сравнительные данные по составу регистрируемых безработных в РТ./ http://www.tatstat.ru/digital/region10/default.aspx
7. Типология и структура рынка труда. Социология./http://www.socioworld.ru/sworlds-77-1.html
8. Трудовые ресурсы Республики Татарстан. Территориальный орган федеральной службы государственной статистики РТ
|
|
|
