 |
Значения ЭДС и активных сопротивлений
|
|
|
|
| Номер группы | Номер схемы | Е1, В | Е2, В | R1, Ом | R2, Ом | R3, Ом |

| ||||||

| ||||||

| ||||||

|
Таблица 2
Значения реактивных сопротивлений при частоте 50 Гц
В омах
| Номер варианта | X1 | X2 | X3 | X4 | X5 | X6 |
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - |
4. Методические рекомендации к выполнению расчетов
4.1. Изображение электрических величин
с помощью комплексных чисел
Комплексным числом A называется выражение вида:
 , (1)
, (1)
где Re A и Im A – действительные числа, j – мнимая единица; Re A – действительная часть числа A, Im A – мнимая часть числа A.
|
|
|
Всякое комплексное число A можно изобразить на координатной плоскости в виде точки A(x; y) с координатами
x = Re A, y = Im A.
 Плоскость, на которой изображаются комплексные числа, называют плоскостью комплексного переменного или комплексной плоскостью. Точкам, лежащим на оси Re (действительная ось), соответствуют действительные числа, точки, лежащие на оси Im (мнимая ось), изображают мнимые числа. Соединив начало координат с точкой A(x, y), получим вектор
Плоскость, на которой изображаются комплексные числа, называют плоскостью комплексного переменного или комплексной плоскостью. Точкам, лежащим на оси Re (действительная ось), соответствуют действительные числа, точки, лежащие на оси Im (мнимая ось), изображают мнимые числа. Соединив начало координат с точкой A(x, y), получим вектор  (рис. 5). Длина вектора
(рис. 5). Длина вектора  называется модулем А комплексного числа А, угол φ, между действительной осью и вектором
называется модулем А комплексного числа А, угол φ, между действительной осью и вектором  , называется аргументом комплексного числа А.
, называется аргументом комплексного числа А.
Имеет место следующее равенство:
 , (2а)
, (2а)
 . (2б)
. (2б)
Тогда
 . (3)
. (3)
Выражения вида (3) называются тригонометрической формой записи комплексного числа.
Если вектор  равномерно вращается с круговой частотой ω, то выражения (2а), (2б) и (3) примут вид
равномерно вращается с круговой частотой ω, то выражения (2а), (2б) и (3) примут вид
 , (4а)
, (4а)
 , (4б)
, (4б)
 . (5)
. (5)
Если, например, задана гармоническая (синусоидальная или косинусоидальная) функция ЭДС
 , (6)
, (6)
где Em – амплитуда, ω – круговая частота, φ – начальная фаза, то ей на комплексной плоскости будет соответствовать равномерно вращающийся вектор, описываемый выражениями (4а) или (4б). Соответственно гармонически изменяющуюся ЭДС (6) можно записать в виде комплексного выражения в тригонометрической
 (7а)
(7а)
или в показательной форме записи
 . (7б)
. (7б)
Аналогично записываются комплексные изображения других электрических величин, значения которых изменяются во времени по гармоническому закону (токи, падения напряжения) или не изменяются (сопротивления). В последнем случае круговая частота ω будет равна нулю.
При одинаковой частоте векторы всех электрических величин вращаются с одинаковой скоростью и их взаимное расположение остается неизменным. Поэтому при анализе соотношений между различными электрическими величинами одной схемы можно считать их неподвижными и опустить в выражениях (7а) и (7б) параметр ωt, т. е. принять, например, время t=0. Получающееся при этом выражение называют комплексной амплитудой. Комплексная амплитуда в тригонометрической и в показательной формах записи имеет вид
|
|
|
 ,
,
 .
.
Для изображения синусоидальных функций чаще пользуются не комплексной амплитудой, а комплексным действующим значением электрической величины
 .
.
Таким образом, если задана синусоидальная функция, то для получения комплексного изображения действующего значения в показательной форме нужно амплитуду разделить на  и умножить на
и умножить на  .
.
Использование комплексных чисел при расчете электрических цепей позволяет заменить действия над мгновенными значениями синусоидально изменяющихся величин действиями над комплексными числами. Таким образом, возникает полная аналогия записей уравнений по законам Ома и Кирхгофа и методов расчета цепей переменного и постоянного тока. Отличие только в том, что в цепях постоянного тока в уравнения входят действительные значения электрических величин (Е, I и т. д.), а в цепях переменного тока – комплексные (Е, I и т. д.).
Расчет цепей переменного тока можно представить в виде следующих трех этапов:
1) прямое преобразование – переход от синусоидальных функций к комплексным величинам;
2) расчет цепи с помощью комплексных чисел;
3) обратное преобразование – переход от комплексных величин к синусоидальным функциям.
4.2. Преобразование схемы цепей переменного тока
 Последовательность преобразования схемы переменного тока не отличается от последовательности преобразования схемы
Последовательность преобразования схемы переменного тока не отличается от последовательности преобразования схемы
а) б) в)
Рис. 6. Преобразование схемы
постоянного тока. Рассмотрим эквивалентное преобразование схемы переменного тока на примере (рис. 6, а).
Сопротивления R 1, X 1 и X4 включены последовательно, заменяем их одним комплексным сопротивлением Z 1:
 ,
,
где модуль комплексного сопротивления Z 1:
 ;
;
аргумент комплексного сопротивления Z 1:
 .
.
Знаку «+» перед реактивным сопротивлением соответствует индуктивный характер сопротивления X, а знаку «–» – ёмкостный.
|
|
|
Аналогично определяются сопротивления Z 2 и Z 3:
 ,
,
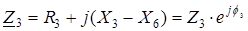 .
.
Сопротивления Z 2 и Z 3 включены параллельно (рис. 6, б). Заменим их одним эквивалентным сопротивлением
 .
.
Сопротивления Z 1 и Z ab (рис. 6, в) включены последовательно. Суммируя их, получаем входное или эквивалентное сопротивление схемы
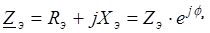 .
.
После определения эквивалентного сопротивления приступаем к определению токов в схеме.
Сначала по закону Ома определяют ток через источник:
 ,
,
где действующее значение тока I 1:
 ,
,
аргумент (начальная фаза) тока I 1:

Затем определяют напряжение U ab, приложенное к разветвленному участку схемы:
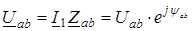
и токи в ветвях:
 ,
,
 .
.
Правильность расчета цепей переменного тока проверяют построением векторной диаграммы и составлением баланса мощностей.
4.3. Расчет цепей переменного тока с двумя источниками
В настоящем задании требуется рассчитать токи в схеме с двумя источниками ЭДС методом наложения, методом контурных токов и методом непосредственного применения законов Кирхгофа.
Метод наложения основан на том, что в электрической цепи с несколькими источниками ЭДС ток в некоторой произвольно выбранной ветви равен сумме частичных токов, каждый из которых обусловлен одним из имеющихся в цепи источников. При использовании этого метода следует рассчитать частичные токи от действия каждого источника ЭДС, заменяя другой проводом без сопротивления (считаем, что источники идеальные и их внутреннее сопротивление равно 0). Принимая E 2=0, находят частичные токи I 1E1, I 2E1, и I 3E1, обусловленные действием источника E 1, а при E 1=0 находят частичные токи I 1E2, I 2E2, и I 3E2, обусловленные действием источника E 2. Искомые токи равны алгебраической сумме (с учетом направлений) частичных токов.
Расчеты частичных токов можно проводить, применяя эквивалентные преобразования схемы в соответствии с пунктом 3.2, или любым другим методом расчета.
При использовании методов контурных токов и непосредственного применения законов Кирхгофа следует составить и решить соответствующие системы уравнений в общем виде, обозначая сопротивления ветвей Z 1, Z 2, Z 3. При этом вид систем уравнений не отличается от такового для цепи постоянного тока. Подставлять вместо ЭДС и сопротивлений их численные значения следует только после нахождения контурных и действительных токов в ветвях в общем виде.
|
|
|
4.4. Составление баланса мощностей
Энергия, потребляемая пассивными элементами электрической цепи, равна энергии, поставляемой в цепь источниками энергии. Таким образом, мощность источников энергии равна мощности потребителей. Это и есть условие баланса мощностей.
Энергетические процессы, протекающие в резистивных (Ri), индуктивных и ёмкостных (Xi) элементах цепи, различны. В резистивных элементах происходит необратимое преобразование электрической энергии в другие виды энергии. Средняя скорость этого процесса определяется активной мощностью P. В реактивных (индуктивных и ёмкостных) элементах происходит периодическое аккумулирование энергии в магнитных и электрических полях, а затем энергия возвращается во внешнюю относительно этих элементов часть цепи. Необратимого преобразования энергии в таких элементах не происходит. Энергетические процессы в индуктивных и ёмкостных элементах определяются реактивной мощностью Q.
Сумма активных мощностей элементов цепи определяется выражением
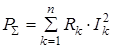 ,
,
где I k – действующее значение тока через k -й элемент цепи с активным сопротивлением RK. Сумма реактивных мощностей элементов цепи определяется как
 ,
,
где I k – действующее значение тока через k -й элемент цепи с реактивным сопротивлением XK. Причем со знаком «+» учитываются мощности индуктивного характера и со знаком «–» – емкостного характера.
Удобно интерпретировать мощность цепи переменного тока как комплексное выражение. В этом случае активная мощность P составляет действительную часть комплексной мощности, а реактивная мощность – мнимую часть:
 .
.
Комплексная мощность источника определяется как
 , (8)
, (8)
где  – комплекс, сопряженный комплексу тока I, протекающего через источник ЭДС E и отличающийся от комплекса I знаком перед мнимой частью (знаком перед аргументом ψ в показателе степени); аргумент комплексной мощности:
– комплекс, сопряженный комплексу тока I, протекающего через источник ЭДС E и отличающийся от комплекса I знаком перед мнимой частью (знаком перед аргументом ψ в показателе степени); аргумент комплексной мощности:
φ=φe – ψ,
Выразив комплексную мощность источника в алгебраической форме, получим
 ,
,
где Pист – активная мощность источника; Qист – реактивная мощность источника.
При нескольких источниках ЭДС их комплексная мощность равна
 , (9)
, (9)
где  – сопряженный комплекс тока I i, протекающего через источники E i. Тогда активная и реактивная мощности источников:
– сопряженный комплекс тока I i, протекающего через источники E i. Тогда активная и реактивная мощности источников:
|
|
|
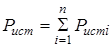 , (10а)
, (10а)
 . (10б)
. (10б)
Полная мощность цепи переменного тока равна произведению действующих значений ЭДС источника Е и тока через источник I:
 . (11)
. (11)
|
|
|


