 |
Очевидно, что значение полной мощности равно модулю комплексной мощности (8).
|
|
|
|
В соответствии с балансом мощностей сумма активных мощностей всех источников энергии должна быть равна сумме мощностей всех резистивных элементов, т.е.
,
а сумма реактивных мощностей всех источников энергии должна быть равна сумме реактивных мощностей всех участков цепи, т.е.
.
Для проверки баланса мощностей схемы, приведенной на рис. 6, а, определяем активные мощности отдельных сопротивлений в ваттах (Вт):
, 
, 
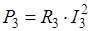
и реактивные мощности в вольт-амперах реактивных (В∙Ар):
, 
, 
.
Находим суммарные активную и реактивную мощности:
, 
.
Полученные результаты сравниваем с действительной и мнимой частями комплексной мощности источников, вычисленной по выражениям (9, 10а, 11б). Решение следует считать правильным, если расхождение значений P и PΣ, Q и QΣ не превышает 1…5%.
4.5. Построение векторных диаграмм
Исходными для построения векторной диаграммы являются комплексные изображения действующих значений токов в ветвях схемы и падений напряжений на её элементах. Для построения векторной диаграммы выбирают масштабы токов и напряжений и в комплексной плоскости по рассчитанным действующим значениям I 1, I 2, I 3, U ab, E и аргументам ψ1, ψ2, ψ3, ψab, φe строят векторы токов, напряжений и ЭДС (рис. 7, где принято φe =0). Затем для проверки определяют напряжение на первом участке
и проверяют в векторной форме выполнение первого
и второго
 |
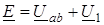
законов Кирхгофа. Решение правильное, если законы Кирхгофа в векторной форме выполняются, т.е. если треугольник (или многоугольник) напряжений получился замкнутым, а ток I 1 равен диагонали параллелограмма, построенного на векторах токов I 2 и I 3.
|
|
|
Рис. 7
Векторную диаграмму можно построить и другим путем, без изображения координат комплексной плоскости. Примем за исходный вектор напряжения U ab на разветвленном участке и отложим его в масштабе горизонтально (рис. 8). Пусть сопротивление ветви 2 (рис. 6, а)
носит активно-индуктивный характер (т. е. X2 >X5). Тогда, вектор тока I 2 отстает по фазе от вектора напряжения U ab на угол φ 2, равный аргументу сопротивления Z 2. Пусть сопротивление ветви 3 с сопротивлениями R 3, X 3 и X 6 носит активно-емкостный характер. Тогда вектор тока I 3 опережает напряжение U ab по
фазе на угол φ 3, равный аргументу сопротивления Z 3. Под углами φ 2 и φ 3 к напряжению U ab откладываем в масштабе векторы токов I 2 и I 3 и на основании первого закона Кирхгофа строим вектор тока I 1 как векторную сумму токов I 2 и I 3.
 |
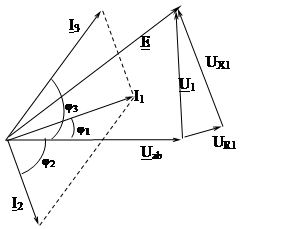Рис. 8
Векторные диаграммы на рис. 7 и 8 аналогичны и полностью совпадут при повороте векторной диаграммы (рис. 7) относительно начала координат на угол ψ ab. При этом наглядно видно, что угол φ 2 (рис. 8) между током I 2 и напряжением U ab будет равен φ 2= ψ ab- ψ 2 (рис. 7). Аналогично φ 3= ψ ab- ψ 3.
Затем определяют напряжения на отдельных сопротивлениях R 1 и X 1 первой ветви:
,
.
По второму закону Кирхгофа
векторная сумма напряжений U ab и U 1R, U 1X должна равняться приложенной к схеме ЭДС. Для проверки этого из конца вектора U ab строим вектор напряжения U R1, который совпадает по направлению с вектором тока I 1, протекающим через это сопротивление. Затем из конца вектора U R1 строим вектор напряжения U X1. Так как в чисто индуктивном сопротивлении ток отстает от напряжения на 90 градусов, то вектор U X1 откладываем перпендикулярно вектору тока I 1. Расчеты выполнены правильно, если многоугольник напряжений, построенный по второму закону Кирхгофа, получается замкнутым.
|
|
|
4.6. Исследование влияния реактивной составляющей входного
сопротивления на ток и мощности, потребляемые от источника
Рассмотрим влияние реактивной составляющей полного сопротивления цепи на примере схемы рис. 9, а.
 |
а) б) в)
Рис. 9
Преобразуем схему к виду рис. 9, б. Ток в схеме рис. 9, б, протекающий через источник ЭДС Е 1, определяется выражением
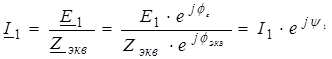, (12)
где
– входное (эквивалентное) сопротивление цепи. Аргумент сопротивления Z экв находится по формуле
. (13)
Ток I 1 будет чисто активным, если его аргумент
(14)
Условие (14) будет выполняться в случае равенства аргументов эквивалентного сопротивления Z экв и ЭДС E 1:
. (15)
Включив реактивное сопротивление Х последовательно с источником ЭДС Е 1 (рис. 9в) и используя выражения (13) и (15), получаем уравнение
. (16)
Решая уравнение (16) относительно X, получаем
. (17)
Отрицательное значение сопротивления X соответствует ёмкостному, а положительное – индуктивному характеру этого сопротивления.
Ток, протекающий через источник E 1 в схеме рис. 9, в, находится аналогично току схеме рис. 9, б, (см. выражение (12)); активную, реактивную и полную мощности, потребляемые от источника, следует находить в соответствии с пунктом 4.4 настоящего пособия.
Коэффициент мощности цепи переменного тока отражает соотношение активной и полной мощностей:
,
где P – активная мощность, потребляемая от источника, S – полная мощность цепи.
4.7. Исследование влияния частоты на ток и мощности,
потребляемые от источника
Реактивные сопротивления, ёмкость, индуктивность и частота тока в цепи связаны выражениями
, (18а)
, (18б)
где L – индуктивность (Гн), С – ёмкость (Ф), XL и XC – соответственно индуктивное и ёмкостное сопротивления, w - круговая (циклическая) частота, связана с частотой f соотношением w = 2pf.
При исследовании схемы, например, рис. 9, а, на первом этапе следует, используя выражения (18а) и (18б), найти значения индуктивностей и ёмкостей всех реактивных элементов цепи. Затем необходимо получить выражения для эквивалентного сопротивления схемы, тока, напряжений, полной, активной и реактивной мощности в общем виде. Меняя частоту ЭДС источника питания E1, следует вычислить реактивные сопротивления элементов и остальные требуемые величины для каждой из частот.
|
|
|
5. Контрольные вопросы
1. Что такое мгновенное значение, начальная фаза и сдвиг фаз?
2. В каких единицах измеряется частота переменного тока? Что такое угловая частота переменного тока и как она связана с периодом?
3. Почему действующее значение переменного тока является одной из его основных характеристик?
4. Что представляет собой индуктивное (ёмкостное) сопротивление и в каких единицах оно измеряется? Как зависит от частоты?
5. Чему равен угол сдвига фаз между напряжением и током для идеального индуктивного (ёмкостного) сопротивления и чем обусловлен этот сдвиг?
6. Что такое активная и реактивная составляющие переменного тока?
7. Какие соотношения справедливы для треугольника сопротивлений и треугольника мощностей?
8. Что понимают под активной и реактивной мощностями в цепи переменного тока? Какие формулы известны для определения этих величин?
9. Что характеризует коэффициент мощности? Почему на практике стараются увеличить коэффициент мощности?
10. В каких цепях возникает резонанс напряжения (тока) и почему он так называется? Каково значение коэффициента мощности цепи при резонансе и почему?
11. В чем сущность символического метода расчета цепей переменного тока?
12. Можно ли на векторной диаграмме изобразить токи, ЭДС и напряжения, изменяющиеся с разными частотами?
13. Что такое комплексное изображение полной мощности?
14. Почему при постоянном токе включение в цепь конденсатора равносильно разрыву цепи, а при переменном токе через емкость проходит ток?
15. Начертить векторную диаграмму напряжений и токов для цепи, состоящей из последовательно соединенных индуктивности, емкости и активного сопротивления.
16. Начертить векторную диаграмму напряжений и токов для цепи, состоящей из параллельно соединенных индуктивности, емкости и активного сопротивления.
17. Сформулируйте и запишите законы Ома и Кирхгофа для цепей переменного тока.
|
|
|
18. Напряжения изменяются по синусоидальному закону 
. Как записать комплекс напряжения в показательной, алгебраической и тригонометрической формах?
19. Найдите эквивалентное сопротивление последовательно (параллельно) соединенных активного, реактивного и емкостного сопротивлений.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Касаткин А.С., Немцов М.В. Электротехника, М.: Энергоатомиздат, 2001.
2. Электротехника./ Под ред. В.Г.Герасимова. – М.: Высшая школа, 1985.
3. Электротехника./ Под ред. В.С.Пантюшина. – М.: Высшая школа, 1976.
4. Сборник задач с решениями по общей электротехнике./ Под ред. В.К.Пономаренко. – М.: Высшая школа, 1972.
|
|
|
