 |
Структурно-топологический анализ систем.
|
|
|
|
При структурном анализе в условиях минимума априорной информации о структуре системы учитывается только факт наличия связи между элементами и её направленность. Поэтому формализация описания структур выполняется с помощью теории графов.
Определение графа. Пусть задано множество элементов V. Граф G(V) считается определённым, если задано семейство сочетаний элементов или пар вида Е=(а,b), где a,b Î V, указывающее какие элементы считаются связанными. Пара Е=(а,b) называется ребром, а элементы a,b - вершинами. Если порядок расположения концов безразличен, то (a,b) - неориентированное ребро, если этот порядок важен, то (a,b) - ориентированное ребро или дуга. Соответственно графы, состоящие из ребер называют неориентированными (рис.1), а из дуг (рис.2) - ориентированными.
Pис.1  Рис.2
Рис.2 
Способы формализованного задания графа.
Существует три способа задания графа.
1.Графический. Наиболее наглядный способ, однако он не может быть использован при решении задачи на ЭВМ.
2.Матричный. Матрица смежности для неориентированного графа имеет вид:

 , где
, где
при наличии связи между вершинами i и j
при отсутствии связи
Для графа рис.1:

Для ориентированного графа элементы a i,j определяются так:
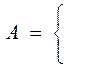
1 если из i можно перейти в j
0 в противном случае
Для графа рис.2:

Если занумеровать рёбра графа, то его можно задать матрицей инцидентности:

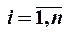 и
и  n — число вершин, m — число рёбер.
n — число вершин, m — число рёбер.
Для неориентированного графа:
 1, если i–я вершина инцидентна j–му ребру
1, если i–я вершина инцидентна j–му ребру
0, если нет связи
Для графа рис.1:

Для ориентированного графа:

1, если i-я вершина есть начало j-го ребра
1, если i-я вершина есть конец j-го ребра
0, если нет связи
|
|
|
Для графа рис.2:
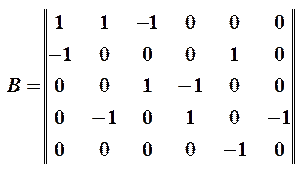
3.Множественный. Для графа G(V) задается множество вершин V и соответствие G, которое показывает как они между собой связаны. Соответствие G(i) показывает множество вершин, в которые можно попасть из i. Для графа рис.2: G(1)=(2,4); G(2)=(5); G(3)=(1); G(4)=(3); G(5)=(4)
Можно задать соответствие G-1 (i) определяющее множество вершин, из которых можно попасть в i.
Для графа рис.2:
G-1(1)=(3); G-1(2)=(1); G-1(3)=(4); G-1(4)=(1,5); G-1(5)=(2)
Основные характеристики графа.
Цепью называется последовательность ребер E1,E2...En, когда каждое из ребер Ei соприкасается одним из концов с ребром Ei+1. Цепь можно обозначить последовательностью вершин, которые она содержит.
Путем называется последовательность дуг, когда конец предыдущей дуги совпадает с началом последующей. Длиной цепи (пути) называют число ребер (дуг), входящих в цепь (путь).
Матрица смежности вершин А является матрицей непосредственных путей графа, имеющих длину раную единице. Общее число транзитных путей от вершины i к вершине j длиной К получается возведением в К-ю степень матрицы А: Ak = Ak+1 * A. Элемент матрицы Ak a(k)i,j определяет число путей длиной k от вершины i к j. Число ребер, инцидентных вершине неориентированного графа, называют степенью вершины P(i).
Структурно - топологические характеристики систем.
Основные структурные характеристики систем можно количественно оценить, используя их модели в виде графов. Рассмотрим основные структурные характеристики систем.
1.Связность структуры. Эта характеристика позволяет выявить наличие обрывов в структуре, висящие вершины.
Для ориентированного графа связность элементов определяется матрицей связности С, где
 , если
, если 
 (1)
(1)
 , если
, если 
Для неориентированного графа связность всех элементов соответствует выполнению условия:
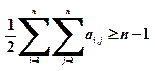
 (2)
(2)
2.Структурная избыточность — это параметр, отражающий превышение общего числа связей над минимально необходимым. Определяется следующим образом:
|
|
|
 (3)
(3)
Для системы с минимальной избыточностью R=0; для несвязных систем R может быть отрицательным.
3.Неравномерность распределения связей в структуре неориентированного графа, имеющего m ребер и n вершин характеризуется показателем:
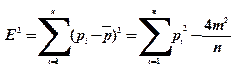 (4)
(4)
Показатель Е2 характеризует недоиспользование возможностей заданной структуры.
4.Структурная компактность - это параметр, отражающий близость элементов между собой:

 (5)
(5)
di,j - минимальная длина цепи между вершинами i и j.
Часто структурная компактность характеризуется относительным показателем:
 (6)
(6)
5.Степень централизации в структуре характеризуется индексом центральности:
 (7)
(7)
 i¹j
i¹j
Индекс центральности меняется в диапазоне от 0 до 1.
6.Ранг элемента позволяет распределить элементы системы в порядке их структурной значимости. Значимость элемента определяется числом его связей с другими элементами. Ранг элемента используется при представлении структуры системы в виде ориентированного графа и может быть вычислен по формуле:

 i=1,n
i=1,n
где a(k)i,j - элементы матрицы Ak (k = 3¸4)
Пример №1. Система задана следующей структурной схемой (рис.3). Рассчитать ее структурно-топологические характеристики и сравнить их с характеристиками структуры типа "кольцевая" (рис.4).
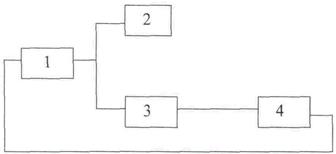
Рис.3. Структурная схема системы.
а)
 |




б) 
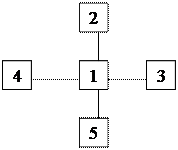 в)
в)
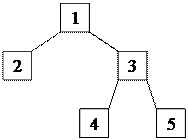 г)
г)
д)

Рис.4.Типовые виды структур для n=5:
а)последовательная; б)кольцевая; в)радиальная; г)древовидная; д)полный граф.
Вначале исходную структурную схему рис.3 представим в виде неориентированного графа(рис.5)
 |
Рис.5.
Типовая кольцевая структура для n=4 соответствует графу рис.6
 |
Рис.6.
Вычислим структурно-топологические характеристики графов рис.5 и рис.6 и сравним их между собой.
Связность структуры
Для графа рис.5 составим матрицу смежности

Проверим условие (2):

-условие связности выполняется.
Аналогично для графа рис.6


-условие связности выполняется.
Структурная избыточность (Расcчитывать по (3)).
Для графа рис.5

Для кольцевой структуры:

Вывод: структура рис.3 обладает в два раза большей избыточностью по сравнению с кольцевой.
|
|
|
Равномерность распределения связей. (Рассчитывать по (4)).
Для графа рис.5

m=5-число ребер
n=4-число вершин
р1=3,р2=2,р3=3,р4=2.
Для графа рис.6:

m=5
n=4
p1=p2=p3=p4=2
В графе рис.6 связи распределяются более равномерно.
Структурная компактность. Оценим ее относительным показателем по(6).
Для графа рис.5: d12=d13=d14=1;
d21=d23=1; d24=2;
d31=d32=d34=1;
d41=d43=1; d42=2.
Тогда:
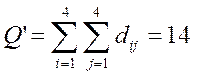

Аналогично, для графа рис.6:

d12=d14=1; d13=2
d21=d23=1; d24=2
d32=d34=1; d31=2
d41=d43=1; d42=2
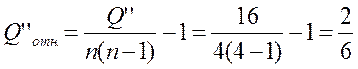
Степень централизации в структуре оценим по индексу центральности d (7).
Для графа рис.5:

 Для графа рис.6:
Для графа рис.6:


Структура рис.5 имеет малую степень централизации, структура рис. 6 абсолютно децентрализована.
Пример 2. Дана структурная схема системы (рис.7.). Ранжировать ее элементы в порядке их структурной значимости.
 |
Рис.7.
Представим систему рис.7 в виде ориентированного графа (рис.8.).
 |

Рис.8.
Матрица смежности графа рис.8 имеет вид:

Для расчета рангов элементов системы вычислим матрицу 



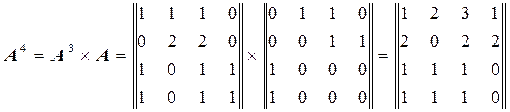
Вычислим ранги элементов системы рис.7 по формуле(8):




Элементы системы в порядке их структурной значимости располагаются следующим образом:
 |
Задание 1. Рассчитать структурно-топологические характеристики данной преподавателем системы и сравнить их с характеристиками одной из типовых структур.
Задание 2. Ранжировать элементы данной преподавателем системы в порядке их структурной значимости.
Варианты
Для системы (рис. а) рассчитать структурно-топологические характеристики и сравнить их с характеристиками одной из типовых структур (последовательная, кольцевая, радиальная, древовидная, полный граф).
Для системы (рис. б) ранжировать элементы в порядке их структурной значимости.
| вар. | Рис. а | Рис. б |
| 1. |  кольцевая
кольцевая
| 
|
| 2. | 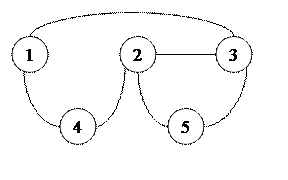 радиальная
радиальная
| 
|
| 3. |  полный граф
полный граф
| 
|
| 4. |  последовательная
последовательная
| 
|
| 5. |  древовидная
древовидная
| 
|
| 6. | 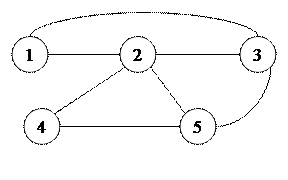 радиальная
радиальная
| 
|
| 7. |  кольцевая
кольцевая
| 
|
| 8. |  полный граф
полный граф
| 
|
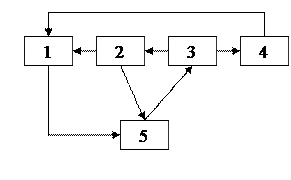
| 9. |  последовательная
последовательная
| 
|
| 10. |  древовидная
древовидная
| 
|
| 11. |  кольцевая
кольцевая
| 
|
| 12. |  полный граф
полный граф
| 
|
| 13. |  последовательная
последовательная
| 
|
| 14. | 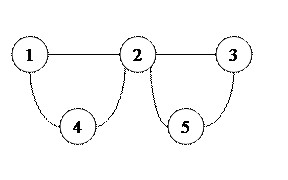 радиальная
радиальная
| 
|
| 15. |  древовидная
древовидная
| 
|
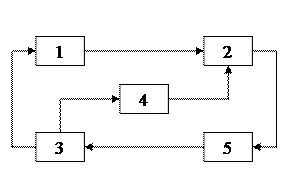
| 16. |  кольцевая
кольцевая
| 
|
| 17. |  полный граф
полный граф
| 
|
| 18. |  последовательная
последовательная
| 
|
| 19. |  кольцевая
кольцевая
| 
|
| 20. |  радиальная
радиальная
| 
|
|
|
|
Лабораторная работа № 4
|
|
|


