Методы первичного описания данных

Для первичного описания исходных данных чаще всего используются таблицы, вариационные ряды и графики. Частным случаем таблицы является таблица кросс-табуляции. Таблицы кросс-табуляции используются для анализа номинативных данных и указывают частоту встречаемости явления. Например, приведенная ниже таблица демонстрирует наличие или отсутствие интереса к математике у студентов факультета психологии СПбАА обоих полов.

	М	Ж
Наличие интереса
Отсутствие интереса
Всего:

Вариационый ряд – упорядоченное отражение распределение значений признака, представляющий двойной ряд чисел и состоящий из обозначения классов и соответствующих частот. В строке признаков можно использовать не только градации (степень выраженности), но и метрические данные, и диапазоны метрических данных.

 

Степень экстраверсии
Частота (кол-во случаев)

Графики (называются также диаграммами) – это чертежи, которые можно использовать для наглядности распределения количественно выраженной величины в выборке. При этом по оси ординат всегда откладывается частота. Ниже дан пример одного из видов графиков, называемого полигоном (представляет собой ломаную линию), демонстрирующего распределение показателей экстраверсии.

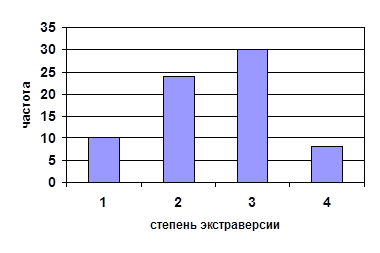
Среди графиков также часто используются гистограммы распределения. Они представляют собой столбиковые диаграммы, при этом каждый столбец опирается на значение признака (интервал значения) переменной. Высота столбца соответствует частоте встречаемости этого значения. Ниже приведен пример гистограммы (значения те же).

Тема 4 Основные понятия математической статистики

Статистическая значимость

Уровень достоверности результата исследования (так называемый р - уровень) – это выраженная количественно степень уверенности, что полученные результаты можно распространить на всю популяцию.

Количественные показатели уровня достоверности, называемого также уровнем статистической значимости, находятся в обратной зависимости от надежности результата. То есть чем выше р – уровень, тем ниже надежность и ниже уровень доверия к найденной зависимости. Так, р = 0,05 является более надежным и более желаемым для исследователя значением, нежели чем р = 0,1.

Таким образом, р - уровень показывает вероятность ошибки, связанной с распространением наблюдаемого результата на всю популяцию. Например, р - уровень = 0,05 показывает, что имеется 5 % вероятности, что найденная в выборке связь между переменными является случайной и характерна только для данной выборки.

Существуют различные мнения относительно того, какая величина р - уровня необходима для определения уровня статистической значимости. Например, Е.В. Сидоренко[1] указывает, что зона значимости результатов начинается только после того, как р - уровень достигнет уровня р = 0,01. Но подобные нормативы приняты по неформальному соглашению среди математиков, физиков и экономистов. В гуманитарных же науках большее распространение получила точка зрения, гласящая, что приемлемой границей статистической значимости является результат р £ 0,05. Именно поэтому мы предлагаем пользоваться классификацией предлагаемой А.Д. Наследовым[2], так как считаем ее более удобной и более популярной среди психологов.

Итак, для определения, является ли результат действительно значимым, рекомендуется пользоваться представленной ниже схемой.

 

Уровень незначимости	Уровень тенденции	Уровень статической значимости	Уровень высокой статистической значимости
	0,1		0,05		0,01

Вероятность ошибки (р - уровень)

 

Уровень значимости (надежность) результатов

Соотношение показателей р-уровня и степени значимости можно представить также в виде таблицы.

 

0,1 > р	результаты статистически незначимы
0,05 < р £ 0,1	результаты значимы на уровне тенденции
р £ 0,05	результаты статистически значимы
р £ 0,01	результаты на уровне высокой статистической значимости

 

Для каждого статистического критерия критические значения р - уровня можно взять из соответствующих специальных таблиц. Знание значения р - уровня необходимо для подтверждения или опровержения статистических гипотез

Статистические гипотезы

Статистические гипотезы бывают: ненаправленные и направленные, которые в свою очередь могут быть нулевыми и альтернативными.

Сначала следует рассмотреть ненаправленные статистические гипотезы. Нулевая гипотеза (обозначается как H₀) – это гипотеза об отсутствии различий между какими-либо показателями. Соответственно, альтернативная гипотеза (обозначается как H₁) – это гипотеза о наличии различий у этих показателей. Например, необходимо выяснить, одинаков ли умственный уровень у учеников школ № 1 и № 2. Перед началом проведения исследования необходимо сформулировать соответствующие гипотезы. В нашем случае нулевая и альтернативная гипотезы будут выглядеть следующим образом.

H₀: уровни умственного развития учеников школ № 1 и № 2 не отличаются друг от друга.

H₁: умственный уровень учеников школ № 1 и № 2 различен.

Направленные гипотезы тоже бывают нулевые и альтернативные. Они говорят не о простом наличии-отсутствии различий, но и об их направлении. В нашем последнем примере они будут выглядеть следующим образом.

H₀: уровень умственного развития учеников школы № 1 не превосходит показатель умственного развития учеников школы № 2.

H₁: умственный уровень учеников школы № 1 превосходит умственный уровень учеников школы № 2.

Отвергать Н₀ и принимать Н₁ следует исходя из следующего принципа: если эмпирическое значение критерия (коэффициента) превышает его критическое значение или равно ему, то отвергается Н₀ и принимается Н₁. О вычислении эмпирических значений и нахождении критических будет сказано позднее. В виде символов реализацию этого принципа можно записать следующим образом:

ЭМП ≥ КР Þ Н₁!

И наоборот: ЭМП < КР Þ Н₀!

Для данного принципа есть исключения. При работе с Т-критерием Вилкоксона, U-критерием Манна-Уитни и G-критерием знаков устанавливается обратное соотношение.

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: