Метод переменных направлений

Рассмотрим двумерное уравнение теплопроводности:

 

dU = LU + f (x,t), x Î G₀₂, t Î [0,t₀]

 dt

U | г = m (x,t)                                                             (1)

U (x,0) = U₀ (x)

LU = LU = (L ₁ +L₂) U, где L _a U = d²U   , a =1,2

dx²

Область G_{0 a} =G₀ = {0<= x _a <= l _a, a =1,2} -прямоугольник со сторонами l₁ и l₂, Г - граница G₀ = G₀ + Г.

В G₀ построили равномерную по xa сетку v _h с шагами h₁ = l₁ /N₁, h₂ = l2 /N₂. Пусть n _h - граница сеточной области w _h, содержащая все узлы на сторонах прямоугольника, кроме его вершин, v _h = w _h + n _h.

Оператор L _a заменим разностным оператором L _a:

 

L _a y = yx _a x _a, L = L ₁ + L ₂

В случае одномерного уравнения теплопроводности неявная схема на каждом слое приводит к разностной краевой задаче вида:

 

A_iy_i-1 - C_iy_i + B_iy_i+1 = -F, i=1,...,N-1

y₀= m ₁                                                                                                                            (2)

y_n= m _N

A_i > 0, B_i > 0, C_i > A_i + B_i

которая решается методом прогонки.

Рассмотрим теперь нашу двимерную задачу в прямоугольнике. Сетку v _h можно представить как совокупность узлов, расположенных на строках i₂=0,1,2,...,N₂, или как совокупность узлов расположенных на столбцах i₁=1,2,...,N₁. Всего имеется N₁+1 столбцов и N₂+1 строк. Число узлов в каждой строке равно N₁+1, а в каждом столбце N₂+1 - узлов.

Если на каждой строке (или столбце) решать задачу вида (2) методом прогонки при фиксированом i₂ (или i₁), то для отыскания решения на всех строках (или столбцах), т.е. во всех узлах сетки, понадобится О(N₁N₂) арифметических действий. Основная идея большинства экономичных методов и состоит в сведении перехода со слоя на слой к последовательному решению одномерных задач вида (2) вдоль строк и вдоль столбцов.

Наряду  с основными значениями искомой  сеточной  функции   y(x,t),  т.е.  с   y = yⁿ и y` = yⁿ⁺¹ вводится промежуточное значение y = y^n+½, которое можно формально рассматривать как значение при t = t_n+½ = t _n+½. Переход от слоя n на слой n+1 совершается в два этапа с шагами 0.5 t.

 

y^n+½ - yⁿ = L ₁ y^n+½ + L ₂ yⁿ + j ⁿ                                                         (3)

T

yⁿ⁺¹ - y^n+½  = L ₁ y^n+½ + L ₂ yⁿ⁺¹ + j ⁿ                                (4)

T

 

Эти уравнения пишутся во всех внутренних узлах x = x_i сетки v _h и для всех t=t_h > 0.

Первая схема неявная по направлению х₁ и явная по х₂, вторая схема явная по х₁ и неявная по х₂. К уравнениям (3),(4) надо добавить начальные условия:

y(x,0) = U ₀(x),   x Î v _h                                                       (5)

и разностно краевые условия, например, в виде:

 

yⁿ⁺¹ = m ⁿ⁺¹ при i₁=0, i₂=N₂                            (6)

y^n+½  = m при  i₁=0, i₂=N₁                           (7)

где m = 1 (m ⁿ⁺¹ + m ⁿ) -  t  L₂(m ⁿ⁺¹ - m ⁿ)                                                              (8)

 2                  4

Т.о., разностная краевая задача (3)-(8) соответствует задаче (1). Остановимся на методе решения этой задачи. Пререпишем (3) и (4) в виде:

2 y - L ₁ y = F, F = 2 y + L ₂ y + j

t                         t                                    (9)

2 y` - L <sub>2</sub> y` = F’, F = 2 y + L ₁ y + j

t                         t

Введём обозначения:

 

x_i = (i₁h₁, i₂h₂)

F = F_i1,i2

y = y_i1,i2

при этом, если в уравнении один из индексов фиксирован, то его не пишем. Тогда (9) можно записать в виде (2), т.е.:

1   y_i1-1 - 2 1   + 1 y_i1 + 1  y_i1+1 = - F_i1

h²₁            h²₁ t          h²₁

i1 = 1,...,N₁-1                                                                (10)

y = m при i1 = 0,N₁

1   y`<sub>i2-1</sub> - 2 1   + 1 y`_i2 + 1  y`_i2+1 = - F_i2

h²₂             h²₂ t            h²₂

i2 = 1,...,N₂-1                                                                (11)

y` = m ` при i2 = 0,N₂

 

Пусть задано у=у ⁿ. Тогда вычисляем   ò F, затем методом прогонки вдоль строк i₂=1,...,N₂-1 решаем задачу (10) и определим y’ во всех узлах сетки w _h, после чего вычисляем F и решаем задачу (11) вдоль столбцов i₁=1,...,N₁-1, определяя y`=yⁿ⁺¹. При переходе от слоя n+1 к слою n+2 процедура повторяется, т.е. происходит всё время чередование направлений.

 

Построение разностных схем

 

Для каждой области МДП - структуры построим консервативную разностную схему, учитывая при этом заданные условия.

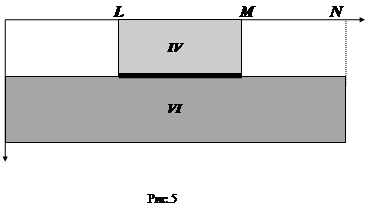
Разобьём данную МДП - структуру на несколько областей следующим образом:

 

 

L                                M       N

 y

 

K ₀

 

K ₁

 

 

x

 

I: j_k0,y = U_n

t. j ^k+½ _i-1,y + 1 +      t   +      t    . j ^k+½ _ij -      t. j ^k+½ _i+1y = Y _ij

2h^*_ih_i                         2h^*_ih_i+1    2h^*_i2h_i                2h^*_ih_i+1

j _k1,y = U_n

где Y _ij = j ^k _ij +  t (L _y j ^k _ij + f ^k _ij)

2

L _y = 1 j ^k_ij+1 - j ^k_ij - j ^k_ij - j ^k_ij-1

   r^*_j     r_j+1              r_j

 

II: j _ij =U₃

   t   . j ^k+½ _i-1,j + 1 +     t         +     t       . j ^k+½ _ij -       t j ^k+½ _i+1,j =

2h^*_ih_i                              2h^*_ih_i+1  2h^*_ih_i               2h^*_ih_i+1

= j ^k _ij +  t L _y j ^k _ij

           2                   ,           0 < i < k0-1 L < j < M

 e_ok  . j ^k+½ _i-1,j + -  e_nn  -  e_ok  . j ^k+½ _ij +   e_n    . j ^k+½ _i+1,j = Y ^* _ij, i=k0

h^*_i-1                        h^*h_i h^*h_i-1                h^*_ih_i

t   . j ^k+½ _i-1,j + 1 +     t       +    t  . j ^k+½ _ij -     t   . j ^k+½ _i+1,j =

 2h^*_ih_i                              2h^*_ih_i  2h^*_ih_i              2h^*_ih_i+1

=   j ^k _ij +  t L _y j ^k _ij - f ^k_ij                         ,k0+1 < i < k1

         2

j ^k _1,j = U_n

 

...

 

III: j _k0,j =U_c

      t   . j ^k+½ _i-1,j + 1 +     t         +     t       . j ^k+½ _ij -       t j ^k+½ _i+1,j =

2h^*_ih_i                            2h^*_ih_i+1  2h^*_ih_i               2h^*_ih_i+1

= j ^k _ij +  t L _y (j ^k _ij - f ^k_ij),                      M+1 < j < N

 2

j _k1,j = U_n

Разностные схемы (I) -(III) решаются методом прогонки в направлении оси OX.

 

y

K₀

 

K₁

       x

 

()

Разностные схемы (IV) -(VI) также решаются методом прогонки в направлении оси OY.

ЛИТЕРАТУРА

1. Годунов С.К.,Рыбинский В.С.: ”Разностные схемы”

2. Кобболд Р.: “Теория и приминение транзисторов”

3. Самарский А.М.: “Теория разностных схем”

4. Самарский А.М.,Николаев Е.С.: “Методы решения сеточных уравнений”

5. Самарский А.А.,Андреев В.Б.: “Разностные методы решения эллиптических уравнений”

6. Калиткин Н.Н.: ”Численные методы”

12	Поделиться:

Воспользуйтесь поиском по сайту: