 |
Оценка качества регулирования
|
|
|
|
Качество любой системы регулирования в большой степени определяется величиной ошибки регулирования, равной разности между управляющим воздействием и регулируемой величиной  Знание мгновенных значений ошибки в течении всего времени работы объекта позволяет наиболее полно судить о свойствах системы регулирования. Однако на этапах проектирования таких знаний недостаточно. Поэтому разработаны другие критерии, позволяющие оценивать показатели качества системы и более того обеспечивать необходимые свойства системе в процессе проектирования.
Знание мгновенных значений ошибки в течении всего времени работы объекта позволяет наиболее полно судить о свойствах системы регулирования. Однако на этапах проектирования таких знаний недостаточно. Поэтому разработаны другие критерии, позволяющие оценивать показатели качества системы и более того обеспечивать необходимые свойства системе в процессе проектирования.
Все критерии и условно разделены на несколько групп:
К первой группе отнесены критерии, использующие для оценки качества величину статической ошибки в различных типовых режимах.
Ко второй группе относятся критерии, определяющие величину запаса устойчивости. Эти критерии позволяют почувствовать, как далеко от границы устойчивости находится система регулирования. Наиболее опасной для системы является колебательная граница устойчивости, когда пара комплексных корней характеристического уравнения попадает на мнимую ось комплексной плоскости. Это возникает в случае чрезмерного увеличения коэффициента усиления разомкнутой системы;
Третья группа критериев определяет быстродействие систем регулирования. Под быстродействием понимается время реагирования системы на появление внешних воздействий. Быстродействие обычно оценивается по времени затухания переходного процесса в системе. Существуют и др. группы критериев [1].
8.1. Статическая точность систем регулирования
Статическая точность определяется на установившемся режиме, который наступает при времени t → ∞. Ошибка регулирования в этом случае называется статической и состоит из двух составляющих:
|
|
|
 (1.113)
(1.113)
где  − часть статической ошибки, определяемая управляющим воздействием g(t);
− часть статической ошибки, определяемая управляющим воздействием g(t);
 − часть статической ошибки, определяемая возмущающим воздействием f(t), рис.1.50.
− часть статической ошибки, определяемая возмущающим воздействием f(t), рис.1.50.

Выполним анализ зависимостей величин статических ошибок для различных режимов изменения управляющего воздействия g(t) при наличии и отсутствия возмущения f(t):
1. В качестве первого типового режима рассмотрим установившееся состояние при постоянных значениях управляющего и возмущающего воздействий.
Пусть управляющее воздействие g(t) = g0, а возмущение f(t) = 0. Для расчета ошибки воспользуемся выражением для передаточной функции системы по ошибке
 , (1.114)
, (1.114)
где  − передаточная функция разомкнутой системы.
− передаточная функция разомкнутой системы.
Для установившегося состояния можно записать
 . (1.115)
. (1.115)
Рассмотрим пример. Пусть регулятор и объект управления являются позиционными звеньями и имеют следующие передаточные функции:
 ,
, 
 (1.116)
(1.116)
С учетом передаточных функций выражение (1.115) принимает вид
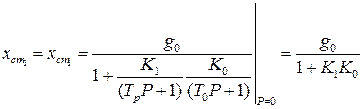
 (1.117)
(1.117)
где 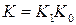 − коэффициент передачи разомкнутой системы.
− коэффициент передачи разомкнутой системы.
Из выражения (1.117) следует, что величина рассматриваемой ошибки  зависит от коэффициента передачи
зависит от коэффициента передачи  . Для уменьшения ошибки необходимо увеличивать этот коэффициент. Однако необходимо помнить, что с увеличением коэффициента
. Для уменьшения ошибки необходимо увеличивать этот коэффициент. Однако необходимо помнить, что с увеличением коэффициента  система приближается к границе устойчивости.
система приближается к границе устойчивости.
Если регулятор имеет передаточную функцию интегрирующего типа  , (1.118)
, (1.118)
то выражение (1.115) примет вид
 .
.
Видно, что ошибка  . Аналогичный результат получается и в случае, когда передаточная функция объекта управления представляется интегрирующим звеном.
. Аналогичный результат получается и в случае, когда передаточная функция объекта управления представляется интегрирующим звеном.
Теперь рассмотрим случай, когда управляющее воздействие g(t) = 0, а возмущение f(t) = f0.
Для расчета ошибки воспользуемся выражением для передаточной функции системы, определяющей связь между ошибкой регулирования и действующим возмущением
|
|
|
 . (1.119)
. (1.119)
Для установившегося состояния можно записать
 (1.120)
(1.120)
Опять рассмотрим пример. Пусть регулятор и объект регулирования имеют передаточные функции, соответствующие выражениям (1.116). С учетом этого выражение (1.120) принимает вид
 . (1.121)
. (1.121)
Видно, что статическая ошибка больше нуля. Величина ошибки, как и в ранее рассмотренном примере (1.116) зависит в основном от коэффициента передачи разомкнутой системы.
Если применить регулятор интегрирующего типа (1.118), то из выражения (1.121) нетрудно понять, что в этом случае статическая ошибка равна нулю.
Из рассмотренных примеров следует, что статическая ошибка характерна для систем регулирования, у которых регулятор в своем составе не имеет интегрирующих звеньев. Далее можно записать полное выражение для статической ошибки (1.113)

2. В качестве второго типового режима для САР рассмотрим изменение управляющего воздействия с постоянной скоростью
g(t) = v*t, (1.122)
где v − постоянный коэффициент.
Этот режим применяется только в следящих системах и в системах программного регулирования.
Примем, что возмущения в системе отсутствуют, т. е.  .
.
С учетом (1.122) выражение для расчета ошибки (1.115) запишется в виде
 .
.
Применяя изображение Карсона − Хевисайда [1]  , можем записать окончательный вид выражения для расчета статической ошибки
, можем записать окончательный вид выражения для расчета статической ошибки

Рассмотрим пример. Пусть передаточные функции регулятора и объекта регулирования соответствуют выражениям (1.116). Тогда выражение для составляющей статической ошибки будет иметь вид

Видно, что составляющая ошибки стремится к бесконечности.
Если в качестве регулятора применить интегрирующее звено, то величина статической ошибки будет конечной:
 ,
,
где коэффициент  называется добротностью системы по скорости.
называется добротностью системы по скорости.
Видно, что имеет место конечная величина ошибки, равная отношению заданной скорости к добротности системы. Данная ошибка называется скоростной. Системы регулирования, у которых регулятор и объект регулирования представлены позиционными звеньями, называют статическими. Если в качестве регулятора применяются интегрирующие звенья, то САР называют астатическими первого или второго порядка, в зависимости от количества интегрирующих звеньев в регуляторе.
|
|
|
Выполненный анализ показывает, что режим движения с постоянной скоростью не должен применяться к статическим системам, так как в установившемся состоянии величина статической ошибки стремится к бесконечности. Этот режим движения применим только к астатическим системам, которые имеют конечную величину статической ошибки, зависящей от добротности системы по скорости.
Случай, когда  , а
, а  ранее рассматривался. Было показано, что, если регулятор системы содержит интегрирующее звено, то составляющая статической ошибки
ранее рассматривался. Было показано, что, если регулятор системы содержит интегрирующее звено, то составляющая статической ошибки  . Следовательно, в рассматриваемых астатических САР эта составляющая не формирует статическую ошибку.
. Следовательно, в рассматриваемых астатических САР эта составляющая не формирует статическую ошибку.
3. Третьим типовым режимом, применяемым в САР, является движение по гармоническому закону:
 g(t) = gmax sin(ωkt),
g(t) = gmax sin(ωkt),
где gmax − максимальная величина управляющего воздействия g(t),
ωк − частота гармонического закона.
В данном анализе возмущающие воздействия могут отсутствовать или иметь постоянные значения. Случай постоянства возмущений приводит, как и в рассмотренных выше первом и втором типовых режимах, к появлению некоторой постоянной составляющей ошибки  .
.
Запишем уже известное выражение для ошибки


В линеаризованной системе при гармоническом управляющем воздействии ошибка в установившемся режиме будет также изменяться по гармоническому закону с частотой ω = ωк, т.е.
 =
=  sin(ωkt+ψ).
sin(ωkt+ψ).
Поэтому точность САР в этом режиме оценивается по амплитуде ошибки, которая может быть найдена по выражению
 .
.
Так как предполагается, что хmax << gmax, то  >> 1. Следовательно, можно записать, что
>> 1. Следовательно, можно записать, что
 (1.123)
(1.123)
где  − модуль частотной передаточной функции разомкнутой системы при частоте ω = ωk.
− модуль частотной передаточной функции разомкнутой системы при частоте ω = ωk.
Формула (1.123) позволяет вычислить амплитуду ошибки в установившемся режиме. Для этого необходимо иметь либо аналитическое выражение для передаточной функции разомкнутой системы, либо экспериментальную амплитудно-частотную характеристику.
Выражение (1.123) позволяет сформулировать требования к АЧХ, которые необходимо выполнить при расчете систем регулирования для обеспечения заданной точности. Для этого по заданному значению амплитуды управляющего воздействия gmax и допустимой амплитуде ошибки  вычисляется требуемое значение Ак=
вычисляется требуемое значение Ак=  . Далее необходимо величину Ак отложить на графике АЧХ при частоте ω = ωк. Полученная точка Ак называется контрольной точкой. Для того, чтобы амплитуда ошибки в системе не превосходила допустимого значения
. Далее необходимо величину Ак отложить на графике АЧХ при частоте ω = ωк. Полученная точка Ак называется контрольной точкой. Для того, чтобы амплитуда ошибки в системе не превосходила допустимого значения  линия АЧХ должна проходить не ниже контрольной точки Ак.
линия АЧХ должна проходить не ниже контрольной точки Ак.
|
|
|
8.2. Оценка запаса устойчивости и быстродействия САР
Оценку запаса устойчивости и быстродействия САР можно выполнить по виду кривой переходного процесса (рис.1.51), возникшего в результате приложения к системе типового внешнего воздействия.
В качестве такого воздействия обычно рассматривается единичный скачок. В этом случае кривую переходного процесса называют переходной характеристикой системы.
Переходная характеристика может строиться для регулируемой величины  или для ошибки регулирования
или для ошибки регулирования  .
.
Склонность системы к колебаниям и запас устойчивости могут быть охарактеризованы величиной перерегулирования
σ % = [ymax− y(∞)] / y(∞)*100%,
где у(∞) − установившееся значение регулируемой величины, после завершения переходного процесса.
Считается, что запас устойчивости достаточен, если величина перерегулирования не превышает 10 ¸ 30 %. Быстродействие системы может определяться по длительности переходного процесса  .
.

Рис.1.51. Кривая переходного процесса
Длительность переходного процесса определяется как время, протекающее от момента приложения на вход единичного скачка до момента, после которого имеет место неравенство
| y(t) − y(∞)| £ ∆,
где ∆ − заданная малая постоянная величина, представляющая собой допустимую ошибку, ∆ 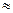 (.01 ¸.05) у(∞) [2].
(.01 ¸.05) у(∞) [2].
Иногда в дополнение к величине перерегулирования задается допустимое число колебаний, которое может наблюдаться в течение времени переходного процесса. Количество колебаний должно составлять 1¸3.
Необходимый запас устойчивости, и быстродействие системы достигается в процессе расчета САР. Для расчета широко применяются частотные и корневые критерии и показатели качества регулирования.
Под частотными критериями понимают такие критерии, которые для оценки качества САР не опираются на формы переходных процессов, а используют для этого некоторые частотные свойства системы.
Частотные критерии наиболее разработаны для оценки запаса устойчивости. Запас устойчивости предлагается определять по удалению амплитудно-фазовой частотной характеристики разомкнутой системы (рис.1.52) от точки (− 1, 0). Для этого вводятся понятия запаса устойчивости поамплитуде (модулю) и запаса устойчивости по фазе.
|
|
|
Для общего случая условной устойчивости, изображенного на рис.1.52, запас устойчивости по амплитуде определяется расположением на вещественной оси комплексной плоскости точек  и
и 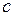 :
:
 = 20 lg
= 20 lg  ;
; 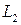 = 20 lg
= 20 lg  .
.
|


Запас устойчивости по амплитуде тем больше, чем больше  и
и  . В хорошо демпфированных системах величины
. В хорошо демпфированных системах величины  и
и 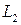 находятся в диапазоне 6 ¸ 20 дб. В случае абсолютной устойчивости имеет смысл только величина
находятся в диапазоне 6 ¸ 20 дб. В случае абсолютной устойчивости имеет смысл только величина  .
.
Запас устойчивости по фазе (Рис.1.52) характеризует удаление АФЧХ по дуге окружности единичного радиуса от точки с координатами (−1,j,0) и соответствует углу μ между отрицательным направлением действительной оси и лучом, проведенным через начало координат и точку пересечения годографа характеристики с окружностью единичного радиуса. Величина запаса устойчивости по фазе определяется по выражению  μ = 180˚ + ψ, где ψ − аргумент (смещение, сдвиг по фазе) частотной передаточной функции разомкнутой системы, соответствующий амплитуде равной единице (точка b на рис.1.52).
μ = 180˚ + ψ, где ψ − аргумент (смещение, сдвиг по фазе) частотной передаточной функции разомкнутой системы, соответствующий амплитуде равной единице (точка b на рис.1.52).
В хорошо демпфированных системах запас по фазе составляет 30¸60˚.
Недостатком рассмотренного частотного критерия является то, что для определения запаса устойчивости необходимо задавать два числа: μ и 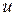 .
.
Более удобно запас устойчивости определять по показателю колебательности. Показателем колебательности называется максимальное значение ординаты Ммах амплитудно - частотной характеристики замкнутой системы (рис.1.53) при начальной ординате, равной единице, т. е. относительная высота резонансного пика.
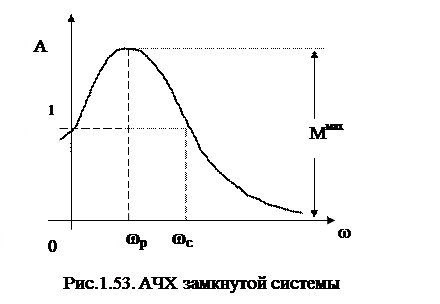
Чем меньше запас устойчивости, тем больше склонность системы к колебаниям и тем выше резонансный пик. Допустимое значение для показателя колебательности определяется на основании опыта эксплуатации систем регулирования. Считается, что в хорошо демпфированных системах регулирования показатель колебательности не должен быть больше 1.1¸1.5. Однако, в отдельных случаях допускается величина Ммах =2¸2.5 [2].
Корневые критерии качества опираются на существующую связь характера и качества переходных процессов в системе автоматического регулирования от расположения корней характеристического уравнения на комплексной плоскости. Поэтому можно сформулировать требования по запасу устойчивости и быстродействию системы посредством наложения условий на расположение корней характеристического уравнения. Заметим, что влиять на расположение корней можно только через коэффициенты характеристического уравнения:
 (1.124)
(1.124)
Решение данного уравнения содержит  - корней:
- корней:  Уже известно, что корни могут быть вещественными и комплексными типа
Уже известно, что корни могут быть вещественными и комплексными типа 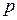 = − α ± jb. Колебания в системе будут наблюдаться, если в решении характеристического уравнения будет присутствовать хотя бы один комплексный корень. Склонность системы к колебаниям может характеризоваться отношением мнимой части корня к его вещественной части Это отношение называют колебательностью
= − α ± jb. Колебания в системе будут наблюдаться, если в решении характеристического уравнения будет присутствовать хотя бы один комплексный корень. Склонность системы к колебаниям может характеризоваться отношением мнимой части корня к его вещественной части Это отношение называют колебательностью
μ=  . (1.125 )
. (1.125 )
Если в решении характеристического уравнения присутствует несколько комплексных корней, то для определения колебательности системы необходимо брать отношение (1.125) для тех корней, для которых это отношение наибольшее.
Колебательность системы связана с другим корневым показателем запаса устойчивости − затуханием. Рассмотрим эту связь. Комплексные сопряженные корни дают в выражении для переходного процесса, например для ошибки регулирования, член вида
x(t) = Ce – αt sin (bt+ψ).
 . Через один период Т = 2π/b амплитуда С2 = Сe – α (t1+ 2π /b) = C1e - 2π α/b = C1e -2π /μ.
. Через один период Т = 2π/b амплитуда С2 = Сe – α (t1+ 2π /b) = C1e - 2π α/b = C1e -2π /μ.
Затуханием за период называют величину
x = 
Эта величина обычно выражается в процентах. Поставляя значение амплитуды С2, получаем x =1 − e−2π/μ или μ = 2π / ln [1/(1−x)].
Обычно в системах автоматического регулирования допускается затухание за период не менее чем 90 ¸ 98 %. Так, например, если x = 98 %, то колебательность при этом составит
μ = 2π / ln 50 ≈ π/2 = 1.57.
Если x =90 %, то колебательность μ ≈ 2.72 [2].
Для оценки быстродействия системы может использоваться показатель, называемый степенью устойчивости. Под степенью устойчивости ή понимается абсолютное значение вещественной части ближайшего к мнимой оси корня (рис.1.54).

Корни характеристического уравнения, расположенные ближе к мнимой оси дают в переходном процессе (1.102) составляющие, которые затухают наиболее медленно, так как эти корни имеют наименьшую по абсолютной величине вещественную часть. В большинстве случаев переходный процесс можно считать завершенным после затухания составляющей, соответствующей ближайшему к мнимой оси корню. Если ближайшим является вещественный корень, то составляющая в переходном процессе, определяемая этим корнем будет иметь вид 

 = C
= C  e –
e – 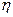 t. Приняв в конце переходного процесса
t. Приняв в конце переходного процесса 

 = ΔC
= ΔC  , где Δ = 0.01 ¸ 0.05, можно получить приближенную зависимость между степенью устойчивостью и временем переходного процесса:
, где Δ = 0.01 ¸ 0.05, можно получить приближенную зависимость между степенью устойчивостью и временем переходного процесса:
tn ≈  ln Δ −1. (1.126)
ln Δ −1. (1.126)
Так, например, если принять Δ =.05, то время переходного процесса tn ≈  ln2 = 3
ln2 = 3  . (1.127)
. (1.127)
Если ближайшими к мнимой оси является пара комплексных корней  , то составляющая в переходном процессе, определяемая этими корнями будет
, то составляющая в переходном процессе, определяемая этими корнями будет  =
=  sin(bt + ψ). Несмотря на присутствие в этой составляющей гармонической функции формула, устанавливающая связь между степенью устойчивости и временем переходного процесса практически будет совпадать с выражением (1.127).
sin(bt + ψ). Несмотря на присутствие в этой составляющей гармонической функции формула, устанавливающая связь между степенью устойчивости и временем переходного процесса практически будет совпадать с выражением (1.127).
Для систем невысокого порядка степень устойчивости можно найти без вычисления корней характеристического уравнения. С этой целью в уравнении (1.124) необходимо перейти к новой переменной 
 . Подставив в уравнение (1.124)
. Подставив в уравнение (1.124) 
 , получим так называемое смещенное уравнение
, получим так называемое смещенное уравнение






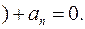
Раскрывая скобки и группируя члены по степеням переменной  , получаем
, получаем
 (1.128)
(1.128)
Это уравнение соответствует смещению осей на плоскости корней влево на величину  (рис.1.54). В результате один (рис.1.54,а) или два (рис.1.54,б) корня попадают на ось мнимых, что соответствует границе устойчивости.
(рис.1.54). В результате один (рис.1.54,а) или два (рис.1.54,б) корня попадают на ось мнимых, что соответствует границе устойчивости.
Для вычисления степени устойчивости необходимо применить к смещенному уравнению (1.128) любой критерий устойчивости и определить, при каком значении  =
=  получается граница устойчивости. Однако, если характеристическое уравнение имеет порядок выше второго, то задача расчета степени устойчивости оказывается не менее сложной, чем расчет корней характеристического уравнения. Например, если в уравнении (1.128) принять
получается граница устойчивости. Однако, если характеристическое уравнение имеет порядок выше второго, то задача расчета степени устойчивости оказывается не менее сложной, чем расчет корней характеристического уравнения. Например, если в уравнении (1.128) принять  , то смещенное уравнение принимает вид:
, то смещенное уравнение принимает вид:
 (1.129)
(1.129)
где 
 ,
,

 2
2 

 ,
,
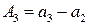


 2
2 
 3.
3.
Видно, что для вычисления степени устойчивости (как и для вычисления корней исходного характеристического уравнения) необходимо решать алгебраическое уравнение третьей степени. Если характеристическое уравнение будет иметь пятый порядок, то для расчета степени устойчивости необходимо будет решать алгебраическое уравнение пятого порядка и т.д. В связи со сложностью решения алгебраических уравнений применение формулы (1.127) для расчета времени переходного процесса оказывается проблематичным.
Однако, применение степени устойчивости оказывается перспективным в задаче обеспечения требуемого быстродействия, возникающей при проектирования системы.
Пусть смещенное уравнение (1.128) относится к проектируемой системе. Этап проектирования соответствует расчету области устойчивости. Для придания системе требуемого быстродействия необходимо выполнить следующее:
 задать требуемое время переходного процесса
задать требуемое время переходного процесса  и по формуле (1.127) вычислить величину
и по формуле (1.127) вычислить величину 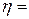
 .;
.;
 по формулам (1.129) с учетом
по формулам (1.129) с учетом  рассчитать коэффициенты
рассчитать коэффициенты  ;
;
 изменяя переменные параметры, в плоскости которых строилась область устойчивости, необходимо переместить рабочую точку на границу устойчивости.
изменяя переменные параметры, в плоскости которых строилась область устойчивости, необходимо переместить рабочую точку на границу устойчивости.
После выполнения указанных действий полученная система регулирования будет иметь время переходного процесса равное  и соответствующие значения переменных параметров.
и соответствующие значения переменных параметров.
Диаграмма Вышнеградского (рис.1.55) позволяет существенно облегчить процесс проектирования систем управления. Несмотря на то, что диаграмма разработана для систем, имеющих характеристическое уравнение третьего порядка, ее применение может существенно облегчить расчет показателей качества и для систем более высокого порядка.
Рассмотрим характеристическое уравнение третьего порядка
 (1.130)
(1.130)
Данное уравнение приводится к нормированному виду,

где 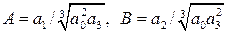
называются параметрами Вышнеградского, а 
 − это новая переменная, введенная в уравнение (1.130), вместо переменной
− это новая переменная, введенная в уравнение (1.130), вместо переменной 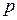 .
.
Диаграмма расположена в плоскости параметров А и В (рис.1.55) и содержит несколько основных кривых линий. Первая линия − граница устойчивости (колебательная). Уравнение границы: АВ = 1, при А > 0 и В > 0. Это равнобокая гипербола, для которой оси координат служат асимптотами.
|
  |
|
|      
| ||||||||||
| 
|
| |||||||||||

| 
| 
|     
| ||||||||||

|
|
|
|


Рис. 1.56. Формы кривых переходных процессов
Область устойчивости находится выше этой кривой. Область устойчивости разбита на три части. На рисунке этим частям даны названия: 1-ая, 2-ая и 3-я области. В каждой области размещена схема расположения корней характеристического уравнения на комплексной плоскости, а на рис. 1.56 приведены типовые для областей формы переходных процессов. Точка С имеет координаты А=3 и В=3. Эта точка является общей для всех областей. Уравнения кривых, разделяющих область устойчивости, в данном материале не рассматриваются. При необходимости эти уравнения можно найти в известной литературе [1].
Диаграмма построена Вышнеградским в 1876 году в работе, которая положила начало развитию теории автоматического регулирования. На диаграмме показаны схемы расположения корней внутри каждой из трех частей области устойчивости. В области 3, где все корни вещественные, в зависимости от начальных условий получаются только апериодические переходные процессы. Формы таких процессов показаны на рис.1.56. Область 3 носит название области апериодических процессов. В областях 1 и 2, где имеется один вещественный корень и пара комплексных, переходные процессы будут иметь соответственно формы, показанные на первых двух графиках рис.1.56. В области 1 быстрее затухает экспонента, и поэтому переходный процесс будет определяться в основном колебательной составляющей. Это будет область колебательных процессов. В области 2, наоборот, быстрее затухает колебательная составляющая. Это будет область монотонных процессов. В последующие годы диаграмма получила дальнейшее развитие. Для более точного определения формы переходного процесса на плоскость диаграммы нанесены вспомогательные линии, разбивающие области 1, 2 и 3 на еще более мелкие части. Это линии равной степени устойчивости  = соnst, линии равного затухания переходных процессов x = const и др. Подробнее об этих линиях в [1].
= соnst, линии равного затухания переходных процессов x = const и др. Подробнее об этих линиях в [1].
8.3.Учет начальных условий при расчете переходных процессов
Переходный процесс возникает в системе при подаче на ее вход внешнего воздействия. Дифференциальное уравнение обыкновенной линейной системы автоматического регулирования, записанное для регулируемой величины  имеет вид:
имеет вид:
 (1.131)
(1.131)
 ,
,
где р =  - алгебраический оператор дифференцирования,
- алгебраический оператор дифференцирования,
g(t) – управляющее воздействие.
Уже отмечалось, что решение данного уравнения  состоит из двух частей общего
состоит из двух частей общего 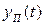 и частного
и частного 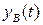 , т.е.
, т.е.
 (1.132) Общее решение представляет собой решение однородного уравнения
(1.132) Общее решение представляет собой решение однородного уравнения
 . (1.133) Это решение имеет вид
. (1.133) Это решение имеет вид
 , (1.134)
, (1.134)
где С1, С2 … Сn - произвольные постоянные, зависящие от начальных условий процесса, а 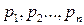 корни характеристического уравнения (1.106).
корни характеристического уравнения (1.106).
Частное решение 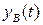 определяется правой частью уравнения (1.104) и соответствует установившемуся режиму, который наступает после затухания функции
определяется правой частью уравнения (1.104) и соответствует установившемуся режиму, который наступает после затухания функции  . Для нахождения полного решения можно записать
. Для нахождения полного решения можно записать
 .
.
Далее требуется найти численные значения для постоянных  и для корней
и для корней  . В большинстве случаев такие вычисления оказываются чрезмерно объемными и трудоемкими. Поэтому для получения кривых переходных процессов в настоящее время применяют численные методы решения дифференциальных уравнений и электронные вычислительные машины.
. В большинстве случаев такие вычисления оказываются чрезмерно объемными и трудоемкими. Поэтому для получения кривых переходных процессов в настоящее время применяют численные методы решения дифференциальных уравнений и электронные вычислительные машины.
Для построения переходных процессов используют различные внешние воздействия. Наиболее распространенными являются типовые воздействия в виде единичной ступенчатой функции g(t) = 1(t) и в виде воздействия, изменяющегося по линейному закону g(t) = v*t (рис.1.57,а и рис.1.57,б). Запишем уравнение (1.131) для случая, когда g(t) =1(t).

|

|

Для численного решения необходимо это уравнение записать с правой частью, в которой оставить только коэффициент 
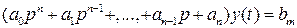 ·1(t). (1.135)
·1(t). (1.135)
и систему начальных условий [2]:
 ·1(t),
·1(t),
 ·1(t) −
·1(t) −  ,
,
 ·1(t) −
·1(t) −  −
−  (1.136)
(1.136)
.........................
 ·1(t) −
·1(t) −  .
.
В системе (1.136) данные являются начальными значениями для производных  и т.д. Введение начальных условий позволяет учесть влияние отсутствующих в правой части уравнения (1.135) коэффициентов
и т.д. Введение начальных условий позволяет учесть влияние отсутствующих в правой части уравнения (1.135) коэффициентов 
Рассмотрим пример. Пусть уравнение системы имеет  , (1.137)
, (1.137)
где 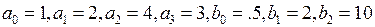 .
.
Очевидно, что  Для интегрирования уравнение (1.137) запишем в виде (1.135)
Для интегрирования уравнение (1.137) запишем в виде (1.135)
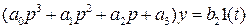 . (1.138)
. (1.138)
Введем обозначение  и запишем (1.138) в форме Коши
и запишем (1.138) в форме Коши




