 |
1.3. Теорема Гаусса.
|
|
|
|
3. 1. Поток вектора через поверхность.
|
|
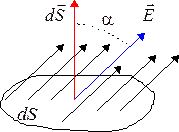
Поток вектора через поверхность - одно из важнейших понятий любого векторного поля и, в частности,
электростатического: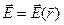 
.
Рассмотрим маленькую площадку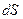 
, в пределах которой вектор
напряженности электрического поля имеет постоянное значение
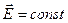, с единичным вектором нормали 
:
,
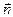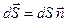. Поток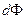 
вектора 
через площадку 
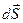определяется как скалярное произведение вектора поля на вектор элементарной площадки:
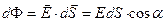. (3. 1)
Т. о., поток вектора есть скалярная величина.
Примечание: для простоты восприятия можно провести аналогию с потоком жидкости, проходящим через сечение 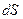, который равен
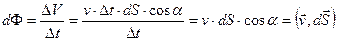
Поток 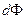можно формально записать несколькими способами:
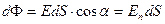, (3. 2)
где подстрочный индекс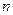 
обозначает проекцию вектора на нормаль.
Понятно, что нормаль 
может иметь два противоположных направления. Для замкнутых поверхностей принято выбирать внешнюю нормаль, т. е. нормаль , направленную наружу охватываемой поверхностью области, что мы и будем подразумевать.
Поток 
вектора через конечную поверхность 
равен
|
|
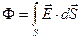. (3. 3)
|
|
3. 2. Поток вектора через замкнутую поверхность.
а). Рассмотрим сначала точечный заряд, окруженный сферической поверхностью с центром в точке нахождения заряда. Т. к. для любого элемента рассматриваемой поверхности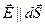 
, то
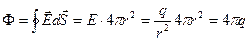(3. 4)
|
|
|
|
|
б) Возьмем теперь произвольную замкнутую поверхность , такую например, как изображена на нижнем рисунке, и сосчитаем поток вектора через элемент поверхности 
в элемент телесного угла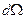 
:
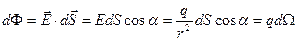, (3. 5)
где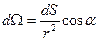 
– телесный угол, который может принимать как положительные, так и отрицательные значения в зависимости от направления нормали (значения угла 
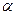), т. е. является величиной алгебраической. Из рисунка видно, что входящий и один из выходящих через поверхности, ограниченные телесным углом 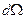, потоков «компенсируют» друг друга, так что отличным от нуля остается только один выходящий в телесном угле 
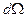поток. Тогда полный поток вектора через произвольную замкнутую поверхность равен
(3. 6)
|
|
Т. о., полученный результат не зависит ни от положения заряда внутри пространства, ограниченного поверхностью , ни от выбора самой поверхности.
Из проведенного рассмотрения, в частности, следует, что для заряда 
, находящегося вне объема, ограниченного замкнутой поверхностью , поток вектора через эту поверхность равен нулю: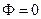 
.
|
|
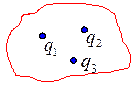
в). Пусть поле создается произвольной системой зарядов. Тогда всю систему можно разбить на точечные заряды 
и для каждого из них в отдельности провести ту же процедуру вычисления. Пользуясь принципом суперпозиции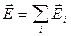 
, получим, что уравнение 
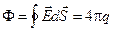может быть обобщено для любой системы зарядов, расположенных произвольным образом, причем стоящий в правой части уравнения заряд будет складываться только из зарядов, находящихся внутри объема, ограниченного рассматриваемой замкнутой поверхностью .
Т. о., получаем
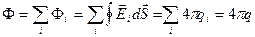, (3. 7)
т. е. из геометрического правила сложения векторов 
следует, что их потоки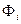 
, как и заряды , складываются алгебраически.
Итак, электростатическая теорема Гаусса:
|
|
|
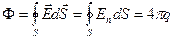(3. 8)
где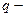 
суммарный заряд внутри поверхности .
Поток вектора сквозь замкнутую поверхность равен с точностью до множителя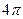 
(полный телесный угол) алгебраической сумме зарядов, охватываемых этой поверхностью.
Отметим еще раз, что расположение зарядов в объеме, ограниченном поверхностью , не играет никакой роли, т. е. поток вектора обладает замечательным свойством – зависит только от алгебраической суммы зарядов, охватываемых этой поверхностью. Если передвинуть заряды, не пересекая поверхности , то поток вектора через эту поверхность останется прежним, хотя само поле может весьма существенно измениться. Заряды, расположенные вне объема, ограниченного замкнутой поверхностью , не вносят вклада в величину потока 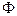, ибо, если говорить на геометрическом языке, сколько силовых линий входит в объем сквозь замкнутую поверхность, столько этих линий и выходит.
Для непрерывного распределения заряда с объемной плотностью 
, зависящей от координат, имеем
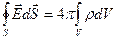(3. 9)
Уравнение (3. 9) представляет собой запись одного из уравнений Максвелла в интегральной форме (за исключением того факта, что вместо вектора индукции электрического поля 
стоит напряженность ). Заметим, что теорема Гаусса является следствием закона Кулона. Она справедлива для всех векторных полей, у которых точечные источники поля создают напряженность, обратно пропорциональную квадрату расстояния от источника 
(центральные поля). В частности, она справедлива для полей тяготения.
Примечание. В СИ: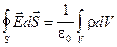 
3. 3. Применение теоремы Гаусса для расчета полей.
Рассмотрим практическое применение теоремы Гаусса для расчета электрических полей.
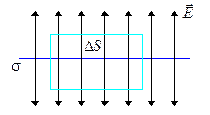
а) Поле бесконечной, равномерно заряженной с поверхностной плотностью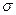 
, плоскости:
|
|
Вектор напряженности поля бесконечной равномерно заряженной плоскости направлен перпендикулярно плоскости, что следует из симметрии рассматриваемой задачи, т. е.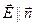 
( 
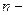нормаль к плоскости) или 
( 
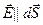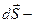элемент поверхности плоскости). В качестве поверхности, которую мы используем для расчета, выберем цилиндрическую поверхность (см. рисунок). Поскольку поле по обе стороны плоскости одинаково, а поток через боковую поверхность цилиндра равен нулю (формально, из-за равенства нулю скалярного произведения и элемента боковой поверхности 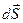), получаем
|
|
|
|
|
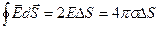, или
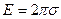. (3. 10)
Примечание. В СИ: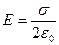 
.
б) Поле бесконечного равномерно заряженного с линейной плотностью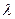 
цилиндра (нити):
Из соображений симметрии следует, что в рассматриваемом случае поле имеет радиальный характер,
т. е. вектор в каждой точке перпендикулярен оси цилиндра, а модуль
вектора напряженности зависит только от расстояния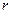 
от оси цилиндра.
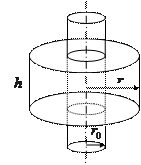
Поэтому в качестве вспомогательной замкнутой поверхности выбираем
поверхность коаксиального прямого цилиндра, как показано на рисунке.
По теореме Гаусса для случая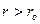 
получаем
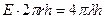, или
, ( 
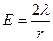). (3. 11)
Если при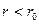 
внутри объема, ограниченного рассматриваемой замкнутой поверхностью, не содержится зарядов, то в этой области 
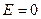, т. е. внутри равномерно заряженного по поверхности круглого бесконечного цилиндра электрическое поле отсутствует.
Примечание. В СИ: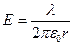 
, ( ). (3. 12)
в). Поле равномерно заряженного шара радиусом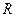 
.
Пусть заряд равномерно распределен по объему шара радиусом 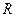. Очевидно, что поле такого шара центрально-симметричное: вектор для любой точки поля проходит через центр шара (при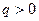 
он направлен от центра, при 
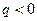- к центру шара), а модуль вектора должен зависеть только от расстояния до центра шара.
|
|
|
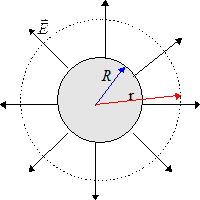
Найдем сначала поле вне шара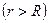 
. Для этого окружим шар концентрической сферой радиусом 
.
|
|
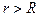По теореме Гаусса
,
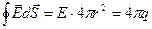откуда
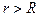, ( ). (3. 13)
Легко убедиться, что тот же результат получится, если вместо объемно заряженного шара рассматривать сферическую поверхность или тот же шар, равномерно заряженный по поверхности зарядом .
Если задана объемная плотность заряда шара , то
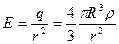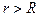, ( ). (3. 13а)
Получим теперь выражение для поля внутри непроводящего шара (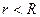 
).
Концентрическая сфера, проходящая внутри шара, охватывает заряд
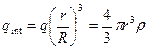, где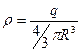 
Поле внутри шара:
.
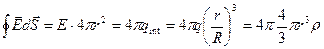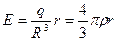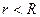, ( ). (3. 14)
Зависимость напряженности электростатического
поля равномерно заряженного по объему шара как функция
расстояния от центра шара приведена на рисунке.
Очевидно, что внутри области, ограниченной равномерно заряженной сферической поверхностью, или шара, равномерно заряженного по поверхности (проводящего шара), поле равно нулю, т. к.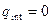 
.
Примечание. В СИ поле внутри шара: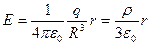 
, ( ).
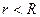К сожалению, число задач, легко решаемых с помощью теоремы Гаусса, весьма ограничено. Её использование для расчета полей эффективно лишь в случаях, где поле обладает специальной симметрией (чаще плоской, сферической, цилиндрической), чтобы можно было найти достаточно простую замкнутую поверхность, окружающую заряды и использовать простой способ вычисления потока вектора .
В тоже время теорема Гаусса имеет фундаментальное значение для теории. Она выражает тот факт, что электрические заряды, заключенные в пространстве, ограниченном замкнутой поверхностью, являются источниками (стоками) электростатического поля
.
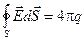При этом поток 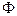вектора напряженности и заряд , ограниченный замкнутой поверхностью , могут рассматриваться как суммарная алгебраическая мощность источников и стоков поля.
Отнеся поток вектора к величине объема 
, ограниченного поверхностью , мы получим среднюю или удельную мощность источников (стоков) поля:
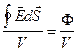. (4. 1)
|
|
|
Удельная мощность источников, вообще говоря, зависит от точки пространства, для которой она вычисляется.
Представим теперь теорему Гаусса применительно к бесконечно малому объему, расширив её возможности как инструмента исследования электрического поля.
|
|
|
