 |
1.5. Работа сил электростатического поля.
|
|
|
|
 |
5. 1. Работа электрического поля. Циркуляция вектора.
Пусть заряд 
в электростатическом поле совершает перемещение
по некоторой криволинейной траектории. Работа 
электрических сил
над зарядом на пути 
находится интегрированием по всем
элементарным участкам пути от точки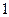 
до точки 
:
, (5. 1)
Из курса механики известно, что любое стационарное поле центральных сил является консервативным или потенциальным. Именно таким свойством обладает электростатическое поле – поле, образованное системой неподвижных зарядов. Поэтому при любом выборе начальной и конечной точек работа сил поля не зависит от формы пути, а определяется только положением этих точек.
Поскольку любое электростатическое поле можно, используя принцип суперпозиции, представить как поле, образованное совокупностью точечных зарядов, полезно сосчитать работу по перемещению пробного заряда в поле неподвижного точечного заряда 
.
Напряженность поля точечного заряда 
, поэтому работа сил этого поля по перемещению заряда находится как
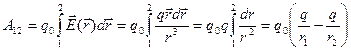. (5. 2)
|
|
Здесь мы использовали, что 
, где 
элементарное приращение длины вектора 
.
Полученное соотношение следует из приведенного рисунка или может быть получено дифференцированием тождества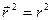 
.
В силу потенциальности электростатического поля работа его сил по замкнутому контуру равна нулю, т. е. можно записать
. (5. 3)
Это одно из фундаментальных уравнений электростатики (часть уравнения Максвелла), являющееся математическим выражением теоремы о циркуляции.
|
|
|
Интеграл, стоящий в левой части уравнения (5. 3), называется циркуляцией вектора 
по замкнутому контуру 
. Интеграл в выражении (5. 3) – линейный, т. е. он берется по некоторой линии (пути).
Термин “циркуляция” происходит от латинского circulatio – круговращение. Он характеризует движение по замкнутой траектории и служит мерой завихренности движения.
Теорема о циркуляции вектора .
Циркуляция вектора в любом электростатическом поле равна нулю.
Всякое векторное поле является потенциальным, если циркуляция этого вектора по любому замкнутому контуру равна нулю.
Примечание. Из теоремы о циркуляции вектора вытекает весьма важный вывод: линии электростатического поля вектора не могут быть замкнутыми.
5. 2. Дифференциальная форма теоремы о циркуляции вектора .
Пусть имеется векторное поле
. (5. 4)
|
|
Чтобы получить математическое выражение теоремы о циркуляции вектора в дифференциальной форме, рассмотрим сначала бесконечно малый контур 
на плоскости 
, ориентированный так, что ось 
направлена на нас (см. рисунок). Направление обхода контура выбрано так, что вектор обойденной площадки направлен вдоль оси z (т. е. в соответствии с правилом буравчика смотрит на нас).
Найдем циркуляцию вектора по бесконечно малому контуру :
. (5. 5)
Минус в двух последних слагаемых появился из-за того, что 
и 
отсчитываются в стороны, противоположные направлениям соответствующих осей. Рассмотрим отдельно слагаемые, соответствующие отрезкам 1 и 2:
|
|
|
. (5. 6)
Здесь 
- элементарная площадка, ограниченная контуром .
Аналогично на отрезках 3 и 4 получаем
. (5. 7)
Итак, обходя весь бесконечно малый контур , получаем
. (5. 8)
Точно так же можно выбрать маленькие площадки, перпендикулярные к осям 
и 
. Определяя циркуляцию вектора по контурам этих площадок, получаем совершенно аналогичные по форме выражения:
. (5. 9)
. (5. 10)
Выражения (5. 8) – (5. 10) можно рассматривать как соответствующие компоненты скалярного произведения некоего вектора, который мы назовем ротором вектора и определим следующим образом:
(5. 11)
и вектора площадки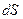 
.
Поскольку сумму правых частей выражений (5. 8) – (5. 10) можно представить как
. (5. 12)
то нормальную к площадке 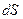составляющую ротора определяем следующим образом:
. (5. 13)
Итак, в каждой точке любого векторного поля, например, поля вектора , можно определить вектор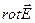 
, направление и модуль которого связаны со свойствами самого поля в данной точке.
Для поверхностей сложной формы направление вектора 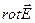определяется тем направлением нормали 
к поверхности 
, при котором достигается максимальное значение величины, определяемой выражением (5. 13), являющееся одновременно модулем вектора .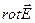
Иная запись ротора может быть формально сделана через оператор 
:
(5. 14)
или в виде определителя:
. (5. 15)
Поскольку для электрического поля циркуляция вектора по любому контуру равна нулю, то исходя из (5. 13), ротор (вихрь) вектора также равен нулю. Т. о., для электростатического поля имеем
. (5. 16)
|
|
|
5. 3. Теорема Стокса.
Вернемся к контуру , ограничивающему поверхность . Разобьем поверхность на одинаковые маленькие площадки 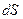, выбрав одинаковые направления обхода вокруг каждой из них. Стягивая эти площадки к точке ( 
) и устремляя длину каждого элементарного контура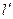 
к нулю ( 
), получим
.
Как видно из рисунка, циркуляция вектора 
по внутренним границам заполняющих поверхность площадок равна нулю. Поэтому отличной от нуля будет лишь циркуляция вектора по контуру , ограничивающему поверхность . В то же время в правой части уравнения мы будем иметь сумму (в пределе – интеграл) произведений площади каждого элементарного участка на нормальную компоненту ( 
).
Т. о., мы приходим к равенству
, (5. 17)
выражающему широко используемую в математических преобразованиях теории поля теорему Стокса.
Теорема Стокса связывает линейный интеграл от произвольного вектора (интеграл слева берется по произвольному замкнутому контуру) с поверхностным интегралом от ротора этого вектора (интеграл справа берется по произвольной поверхности, натянутой на этот контур).
|
|
|
