Прогнозирование надежности изделия

 

Исходные данные. Зависимость наработки устройства до отказа от времени его эксплуатации подчиняется двухпараметрическому закону Вейбулла с параметрами k = 1,6 и b = 600 часов. Требуется вычислить количественные характеристики надежности устройства в интервале времени его работы t 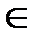[0;1100] часов с дискретностью Δ t = 110 часов и представить результаты в виде графических зависимостей характеристик надежности от наработки.

Решение. В приложении 1 (таблица П.2) приведены формулы для расчета показателей надежности, если распределение его наработки до отказа подчиняется закону Вейбулла. Вычисления будем выполнять в табличной форме (см. таблицу 2). Используемые при этом значения функций ехр(- х^k) и Г (х) табулированы и приведены в [ Корн, Г. Справочник по математике для научных работников и инженеров: определения, теоремы, формулы / Г. Корн, Т. Корн. – М.: Наука, 1984. С. 741].

 

Таблица П2 – Выражения для расчета показателей надежности по известным

Функциям распределения

Закон распределения с плотностью f (t)	Выражение для расчета
Тср	Вероятность безотказной работы R (t)	Интенсивность отказов h (t)
Экспоненциальный	1 / λ	exp(-λ t)	λ
Вейбулла
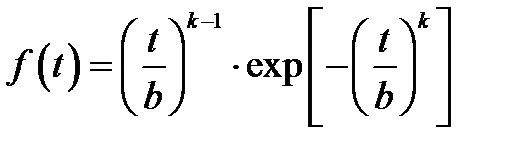
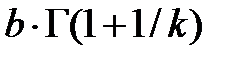
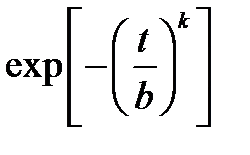
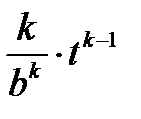
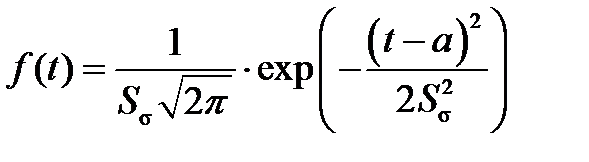
Нормальный	a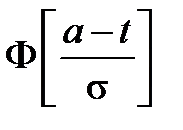
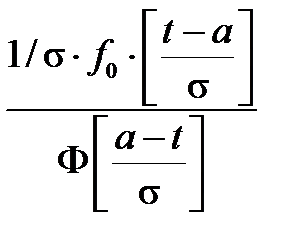
Логарифмический нормальный
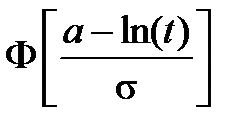
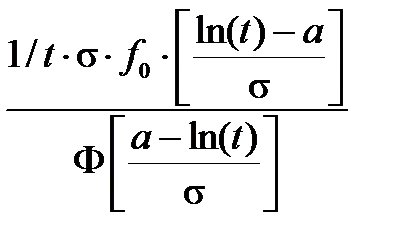
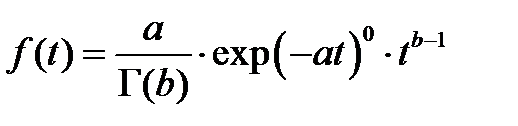
Гамма	b/a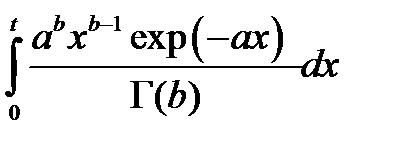

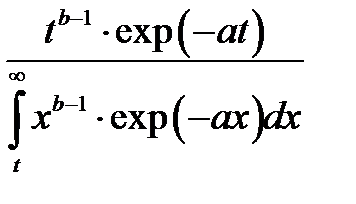
Здесь a, b, λ, σ – параметры вышеуказанных законов распределения; a > 0, b > 0, λ> 0, σ> 0.

 

Рассмотрим порядок вычисления показателей надежности для наработки t = 220 часов (третья строка таблица 2). Вычислим характеристику х = t / b:

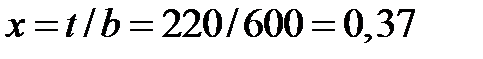
Вероятность безотказной работы R (t) для закона Вейбулла определяется по формуле

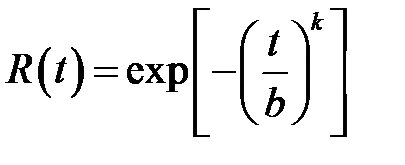
Средняя наработка до отказа 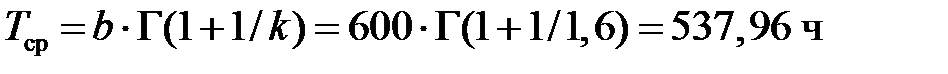. Подставив численные значения t / b и k, получим 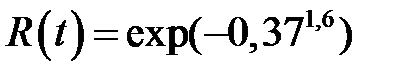. По таблице функции ехр(- х^k) из [ Корн, Г. Справочник по математике для научных работников и инженеров: определения, теоремы, формулы / Г. Корн, Т. Корн. – М.: Наука, 1984.] находим .

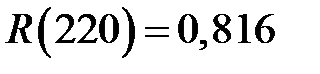Интенсивность отказов для заданного закона определяется из , откуда получаем .

Плотность вероятности отказов для закона Вейбулла находим по формуле (см. таблицу П.2)

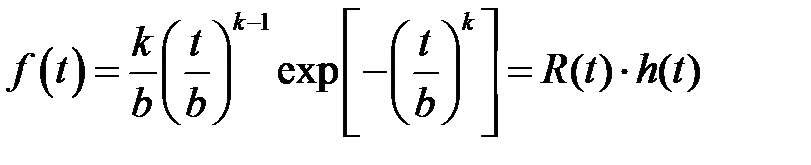
Таблица 2 – Вероятностная оценка количественных показателей надежности

Устройства при распределении наработки по закону Вейбулла

t, ч	t / b	R (t)	h (t),·10-4 ч -1	f (t),·10-4
	0,18	0,938	9,6	9,00
	0,37	0,816	14,6	11,91
	0,55	0,681	18,6	12,67
	0,73	0,546	22,1	12,08
	0,92	0,417	25,3	10,55
	1,1	0,312	28,2	8,80
	1,28	0,227	31,0	7,03
	1,47	0,157	33,6	5,27
	1,65	0,108	36,0	3,88
	1,83	0,072	38,4	2,77

 

Подставив численные значения параметров, получаем 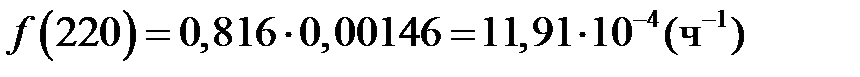. Аналогично ведется расчет для других наработок (см. таблицу 2).

Средняя наработка изделия до отказа вычисляется по формуле

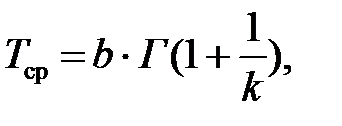
где Г – гамма-функция. В нашем случае 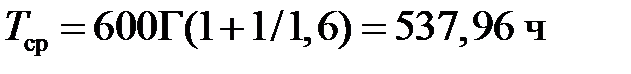, где значение функции Г (1,625) находим по [ Корн, Г. Справочник по математике для научных работников и инженеров: определения, теоремы, формулы / Г. Корн, Т. Корн. – М.: Наука, 1984. С. 741]. На рисунке 2 изображены графики функций R (t), h (t) и f (t). Как видно из рисунка, функция R (t) является убывающей, a h (t) – возрастающей. Функция плотности распределения f (t) наработки до отказа имеет, как правило, куполообразный вид и ее максимуму соответствует мода наработки устройства до отказа Т ₀ ≈ 330 ч.

Другим характерным параметром функции f (t) является средняя наработка до отказа Т_ср ≈ 538 часа: прямая t = Т_ср = const делит площадь под кривой f (t) на две равные части.

Рисунок 2 – Зависимость характеристик надежности изделия
от наработки по закону Вейбулла

 

 

Таблица П.3 – Варианты заданий к задаче № 1

№ вар	N0, штук	(Δ t) i = const, ч	n 1 (Δ t), шукт	n 2(Δ t), шукт	n 3(Δ t), шукт	n 4(Δ t), шукт	n 5(Δ t), шукт
					15:

 

Таблица П.4 – Варианты заданий к задаче № 2

№вар	t max, ч	b, ч	k	№вар	t max, ч	b, ч	k
			1,2				1,6
			1,2				1,6
			1,2				1,6
			1,2				1,8
			1,2				1,8
			1,2				1,8
			1,4				1,8
			1,4				1,8
			1,4				1,8
			1,4				2,0
			1,4				2,0
			1,4				2,0
			1,6				2,0
			1,6		69б0		2,0
			1,6				2,0

 

12	Поделиться:

Воспользуйтесь поиском по сайту: