 |
Решения задач диагностической работы
|
|
|
|
ЕГЭ 2010. Математика. Задача B9. Рабочая тетрадь
Смирнов В.А.
(под редакцией А. Л. Семенова и И.В.Ященко)
М.: Издательство МЦНМО; 2010, 48 стр.
Рабочая тетрадь по математике серии «ЕГЭ 2010.Математика» ориентирована на подготовку учащихся старшей школы для успешной сдачи Единого государственного экзамена по математике в 2010 году. В рабочей тетради представлены задачи по одной позиции контрольных измерительных материалов ЕГЭ-2010.
На различных этапах обучения пособие поможет обеспечить уровневый подход к организации повторения, осуществить контроль и самоконтроль знаний по основным темам стереометрии. Рабочая тетрадь ориентирована на один учебный год, однако при необходимости позволит в кратчайшие сроки восполнить пробелы в знаниях выпускника.
Тетрадь предназначена для учащихся старшей школы, учителей математики, родителей.
http://geometry2006.narod.ru/
Содержание
Введение
Диагностическая работа ……………………………………………………..
Решения задач диагностической работы ……………………………………
Тренировочные работы ………………………………………………………
1. Куб ……………………………………..…………………………………..
2. Параллелепипед ……………………………………………………………
3. Призма ………………………………………………………………………
4. Пирамида ……………………………… …………………………………..
5. Цилиндр, конус, шар ……………………………………… ……………...
6. Вписанные и описанные фигуры в пространстве ………… ……………
Самостоятельные работы …………………………………………………….
Самостоятельная работа 1 ………………………………………………….
Самостоятельная работа 2 ………………………………………………….
Самостоятельная работа 3 ………………………………………………….
|
|
|
Ответы ……………………………………………………………………….
ВВЕДЕНИЕ
Данное пособие предназначено для подготовки к выполнению задания В9 ЕГЭ по математике. Его целями являются:
– показ примерной тематики и уровня трудности геометрических задач, включенных в содержание ЕГЭ;
– проверка качества знаний и умений учащихся по геометрии, их готовность к сдаче ЕГЭ;
– развитие представлений учащихся об основных геометрических фигурах и их свойствах, формирование навыков работы с рисунком;
– повышение вычислительной культуры учащихся, подготовка их к решению геометрических задач с числовым ответом.
Пособие содержит задачи на нахождение объемов и площадей поверхностей пространственных фигур. Оно проверяет уровень развития пространственных представлений учащихся, умения находить объемы и площади поверхностей многогранников, круглых тел и их комбинаций.
Для успешного выполнения предлагаемых задач требуются знания основных формул для нахождения значений геометрических величин пространственных фигур, умения проводить дополнительные построения на изображениях пространственных фигур, работать с формулами, выполнять арифметические действия и преобразования числовых выражений.
Все задачи сопровождаются рисунками, позволяющими лучше понять условие, представить соответствующую геометрическую ситуацию, наметить план решения, при необходимости провести дополнительные построения и вычисления.
Вначале предлагается диагностическая работа, содержащая задачи, разбитые на семь различных типов по две задачи в каждом. Для тех, кто хочет проверить правильность решения предложенных задач или убедиться в верности полученного ответа, приводятся их решения и даются ответы. Затем, для закрепления рассмотренных методов решения задач, предлагаются тренировочные работы, каждая из которых содержит задачи одного типа.
|
|
|
В случае успешного решения этих задач можно переходить к выполнению заключительных самостоятельных работ, содержащих задачи разных типов.
В конце пособия даны ответы ко всем задачам.
По аналогии с рассмотренными задачами можно самим придумывать и решать задачи на нахождение объемов и площадей поверхностей.
Отметим, что лучшим способом подготовки к ЕГЭ по геометрии являются систематические занятия по учебнику геометрии. Данное пособие не заменяет учебника. Оно может быть использовано в качестве дополнительного сборника задач при изучении геометрии, а также при организации обобщающего повторения или при самостоятельных занятиях по геометрии.
Диагностическая работа
1.1. 1.1. Диагональ куба равна 
. Найдите его объем.
 |
1.2. 1.2. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 30. Найдите ребро куба.
 |
2.1. Диагональ прямоугольного параллелепипеда равна 
и образует углы 30о, 45о и 60о с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
 |
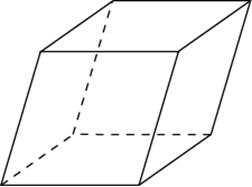
2.2. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60о. Одно из ребер параллелепипеда составляет с этой гранью угол в 60о и равно 2. Найдите объем параллелепипеда.
 |
3.1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
 |
3.2. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
 |
4.1. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
 |
4.2. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности пирамиды.
 |
5.1. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
 |
5.2. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3.
|
|
|
 |
6.1. В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали?
 |
6.2. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
 |
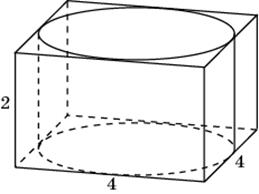
7.1. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объем параллелепипеда.
 |
7.2. В куб с ребром 6 вписан шар. Найдите объем шара, деленный на 
.
 |
Решения задач диагностической работы
1.1. Если ребро куба равно a, то его диагональ равна 
. Отсюда следует, что если диагональ куба равна , то его ребро равно 2 и, значит, объем этого куба равен 8.
Ответ. 8.
 |
1.3. 1.3. Если ребро куба равно x, то площадь его поверхности равна 6 x 2. Если ребро куба увеличить на 1, то его площадь поверхности будет равна6(x+ 1)2. Учитывая, что площадь поверхности куба при этом увеличивается на 30, получаем уравнение 6(x+ 1)2 = 6 x 2 + 30, решая которое, находим x = 2.
 |
Ответ. 2.
2.1. Если диагональ прямоугольного параллелепипеда равна и образует с плоскостью грани угол 30о, то ребро, перпендикулярное этой грани будет равно 
. Аналогично, два других ребра параллелепипеда будут равны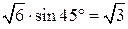 
и 
. Объем параллелепипеда равен 
.
 |
Ответ. 4,5.
2.2. Площадь грани параллелепипеда, являющейся ромбом со стороной 1 и острым углом 60о, равна 
. Высота, опущенная на эту грань, равна 
. Объем параллелепипеда равен 1,5.
 |
Ответ. 1,5.
3.1. Площадь основания треугольной призмы равна 
. Высота призмы равна 5. Объем призмы равен 120.
 |
Ответ. 120.
3.2. Площадь основания отсеченной призмы равна четверти площади основания исходной призмы. Высота отсеченной призмы равна высоте исходной призмы. Следовательно, объем отсеченной призмы равен четверти объема исходной призмы, т.е. равен 8.
|
|
|
 |
Ответ. 8.
4.1. Воспользуемся тем, что если два тетраэдра подобны и коэффициент подобия равен k, то отношение объемов этих тетраэдров равно k 3. Если ребра тетраэдра увеличить в два раза, то объем тетраэдра увеличится в 8 раз.
Ответ. 8.
 |
4.2. Высота боковой грани пирамиды равна 12. Площадь боковой грани равна 60. Площадь боковой поверхности этой пирамиды равна 360.
Ответ. 360.
 |
5.1. Поверхность многогранника состоит из двух квадратов, площадь которых равна 4, четырех прямоугольников, площадь которых равна 2, и двух невыпуклых шестиугольников, площадь которых равна 3. Следовательно, площадь поверхности многогранника равна 22.
 |
Ответ. 22.
5.2. Площадь основания пирамиды равна 27, высота равна 3. Следовательно, объем пирамиды равен 27.
 |
Ответ. 27.
6.1. Так как уровень жидкости в сосуде поднялся в 1,5 раза, то и объем увеличился в 1,5 раза, т.е. стал равен 9. Следовательно, объем детали равен 3.
 |
Ответ. 3.
6.2. Площади поверхностей данных шаров равны 
и 
. Их сумма равна 
. Следовательно, радиус шара, площадь поверхности которого равна этой сумме, равен 10.
Ответ. 10.
 |
7.1. Ребра параллелепипеда равны 4, 4, 2 и, следовательно, его объем равен 32.
Ответ. 32.
 |
7.2. Радиус шара равен 3. Объем шара равен 
, а объем, деленный на равен 36.
 |
Ответ. 36.
Тренировочные работы
1. Куб
1. Диагональ куба равна 
. Найдите его Объем.
|
2. 2. Диагональ грани куба равна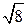 
. Найдите его объем.
 |
3. 3. Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
 |
4. 4. Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?
 |
5. 5. Диагональ куба равна 1. Найдите площадь его поверхности.
 |
6. Площадь поверхности куба равна 8. Найдите его диагональ.
|
7. Диагональ грани куба равна 3. Найдите площадь его поверхности.
|
8. Площадь поверхности куба равна 48. Найдите диагональ грани куба.
 |
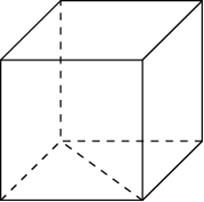9. Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого равны 90о.
 |
Параллелепипед
1. 1. Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
|
|
|
 |
2. 2. Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
|
3. 3. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
 |
4. 4. Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3, 4, 5. Найдите площадь его поверхности.
 |
5. 5. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 52. Найдите третье ребро, выходящее из той же вершины.
|
6. 6. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.
 |
7. 7. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
|
8. 8. Гранью параллелепипеда является квадрат со стороной 1. Одно из ребер параллелепипеда составляет с этой гранью угол в 60о и равно 
. Найдите объем параллелепипеда.
|
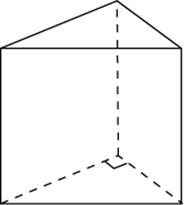
9. 9. Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого равны 90о.
 |
Призма
1. 1. Найдите объем правильной треугольной призмы, все ребра которой равны .
 |
2. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
 |
2. 2. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
 |
4. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 3 и 4, и боковым ребром, равным 5.
 |
6. 6. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
|
7. 7. Найдите боковое ребро правильной четырехугольной призмы, если стороны ее основания равны 3, а площадь поверхности равна 66.
 |
7. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 12, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
 |
8. Объем правильной треугольной призмы равен 6. Каким будет объем призмы, если стороны ее основания увеличить в три раза, а высоту уменьшить в два раза?
 |
9. Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны .
4. Пирамида
1. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна .
 |
3. 3. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
 |
4. 4. Диагональ основания правильной четырехугольной пирамиды равна 8. Боковое ребро равно 5. Найдите объем пирамиды.
 |
5. 5. В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро пирамиды.
 |
6. 6. Стороны основания правильной четырехугольной пирамиды равны 6, боковые ребра равны 5. Найдите площадь поверхности пирамиды.
 |
7. 7. Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
 |
8. 8. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?
 |
9. 9. Объем правильной четырехугольной пирамиды равен 12. Найдите объем пирамиды, отсекаемой от нее плоскостью, проходящей через диагональ основания и середину противоположного бокового ребра.
 |
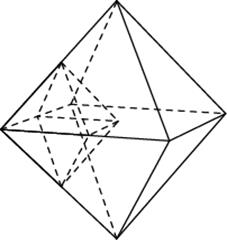
10. 10. Во сколько раз уменьшится объем октаэдра, если все его ребра уменьшить в два раза?
 |
Цилиндр, конус, шар
1. 1. Найдите объем цилиндра, площадь основания которого равна 1, а образующая равна 6 и наклонена к плоскости основания под углом 30о.
 |
2. 2. Цилиндр и конус имеют общие основание и высоту. Найдите объем цилиндра, если объем конуса равен 50.
 |
3. 3. Воду, находящуюся в цилиндрическом сосуде на уровне 12 см, перелили в цилиндрический сосуд, в два раза большего диаметра. На какой высоте будет находиться уровень воды во втором сосуде?
 |
4. Найдите объем конуса, площадь основания которого равна 2, а образующая равна 6 и наклонена к плоскости основания под углом 30о.
 |
4. 4. Объем конуса равен 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите объем отсеченного конуса.
 |
5. 5. Площадь осевого сечения цилиндра равна 
. Найдите площадь боковой поверхности цилиндра.
 |
6. 6. Площадь большого круга шара равна 1. Найдите площадь поверхности шара.
 |
7. 7. Во сколько раз увеличится площадь поверхности шара, если его радиус увеличить в два раза?
 |
9. Радиусы трех шаров равны 3, 4 и 5. Найдите радиус шара, объем которого равен сумме их объемов.
 |
|
|
|
12 |
