 |
Способы задания автомата Миля
|
|
|
|
P, W, S, s0 – задается аналогично автомату Мура.
Функции выхода задаются тремя способами:
a) перечисление
φ:
S1 = φ(S0, P1) – предыдущее воздействие – новое состояние
S2 = φ(S1, P2)
…
Sm-1 = φ(Sm-2, P0)
ψ:
W1 = ψ (S0, P1)
W2 = ψ (S1, P2)
…
Wl-1 = ψ (Sm-1, P0)
b) Табличный способ
| Pj | P0 | P1 | … | Pn-1 |
| Si | ||||
| S0 | S1 | S2 | … | S3 |
| S1 | S2 | S3 | … | … |
| … | … | … | … | … |
| Sm-1 | S0 | … | … | … |
Таблица выходов для ψ
| Pj | P0 | P1 | … | Pn-1 |
| Si | ||||
| S0 | W0 | W1 | … | Wl-1 |
| S1 | W1 | W2 | … | … |
| … | … | … | … | … |
| Sm-1 | W0 | … | … | … |
Две таблицы различны только соединением внутренних клеток, поэтому с целью упрощения их объединяют и приводят в виде так называемой совмещенной таблицы переходов и выходов.
| Pj | P0 | P1 | … | Pn-1 |
| Si | ||||
| S0 | S1/W0 | S2/W1 | … | S3/Wl-1 |
| S1 | S3/W1 | S2/W2 | … | … |
| … | … | … | … | … |
| Sm-1 | S0/W0 | … | … | … |
c) Графический способ
Так как выходной сигнал зависит и от состояния и от входного сигнала, то выходной сигнал приводят на ребре графа.
 | |||
 | |||
Пример (автомат)
P = {P1, P2}
W = {W0, W1}
S = {S0, S1, S2}
s0
1) перечисление
φ:
S0 = φ(S0, P1)
S0 = φ(S2, P2)
S1 = φ(S0, P2)
S1 = φ(S1, P1)
S2 = φ(S1, P2)
S2 = φ(S2, P1)
ψ:
W0 = ψ (S0, P1)
W1 = ψ (S0, P2)
W0 = ψ (S1, P1)
W0 = ψ (S0, P2)
W0 = ψ (S2, P1)
W0 = ψ (S2, P2)
2) Таблица (совмещение переходов и выходов)
| Pj | P1 | P2 |
| Si | ||
| S0 | S0/W0 | S1/W1 |
| S1 | S1/W0 | S2/W0 |
| S2 | S2/W0 | S0/W0 |
3)
|
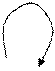
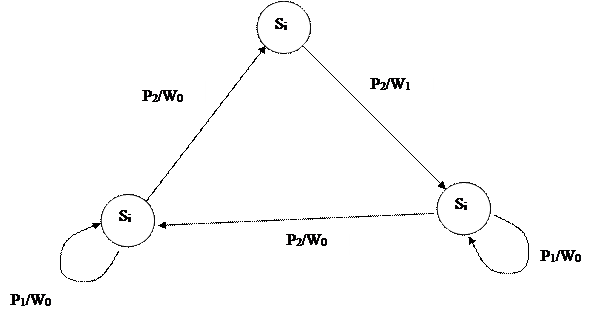 |
Тест:
| ti | t0 | t1 | t2 | t3 | t4 | |
| si | s0 | s0 | s1 | s2 | s2 | s0 |
| Pi | P1 | P2 | P2 | P1 | P2 | |
| Wi | W0 | W1 | W0 | W0 | W0 |
В автомате Мура выходной сигнал определяется только состоянием автомата, следовательно сколь угодно долго автомат будет находиться в некотором состоянии, сколько можно считывать его выходной сигнал соответствующий данному состоянию.
|
|
|
В автомате Миля выходной сигнал зависит не только от состояния, но и от входного сигнала, а следовательно значение выходного сигнала можно считывать лишь в короткие интервалы времени при переходах из одного состояния в другое.
Преобразование автоматов из Миля в Мура и обратно
Понятие эквивалентности автоматов
Два автомата, у которых входные и выходные алфавиты одинаковы или между буквами этих алфавитов можно установить взаимно однозначное соответствие, то их называют эквивалентными если любое входное слово оба автомата перерабатывают в одни выходные, при условии что автоматы находились в начальном состоянии.
Преобразование Мура в Миля
Ar = <Pr, Wr, Sr, s0r, φr, ψr>
Al = <Pl, Wl, Sl, s0l, φl, ψl>
Ar – автомат Мура задан, необходимо найти эквивалентное ему автомат Миля. Al
1) Pl = Pr
2) Wl = Wr
3) Sl = Sr
В общем случае число соответствий Миля может оказаться меньше чем число соответствий Мура, следовательно
Sl <= Sr
4) s0l = s0r
5) в Мура Sr(t+1) = φr(Sr(t), Pr(t))
в Миле Sl(t+1) = φl(Sr(t), Pl(t))
следовательно φl(SiPj) = φ(SjPj)
Новое состояние как в Муре так и в Миле зависит от предыдущего состояния и предыдущего входного сигнала.
Так как во время преобразования Мура в Миля уже установлены условия 1 и 3, то функция переходов при одном и том же воздействии автомата Миля должна совпадать с функцией переходов автомата Мура при тех же воздействиях.
Wl(t+1) = ψl(Sl(t), Pl(t))
Wr(t+1) = ψr(Sr(t+1)) = ψr(φr(Sr(t), Pr(t))
Wl(t+1) = Wr(t+1)
В автомате Миля новое выходное значение зависит от старых состояний и выходного сигнала.
В автомате Мура выходной сигнал зависит от нового состояния, т.к. новое состояние
Sr(t+1) = φr (Sr(t), Pr(t))
Определяется через старое состояние, то подставим
Sr(t+1).
|
|
|
Сравнивая функции выходов автомата Миля и Мура видно, что для обеспечения условий необходимо выходные значения автомата Мура соответствующие новым состояниям, сделать равным выходным значениям автомата Миля полученным на преходах в это состояние.
Техника преобразований.
При преобразовании автомата Мура в Миля необходимо выходные символы, которыми помечены вершины перенести на все входящие дуги в данную вершину.
Пример:
|
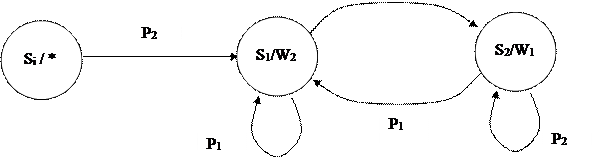 |
Автомат Миля
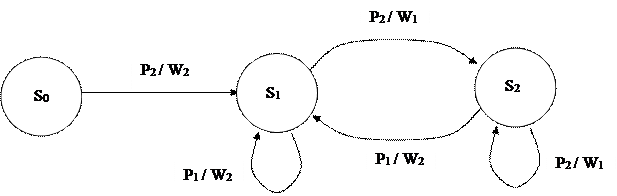
Обратный переход.
|
|
|


