 |
Выбор математической модели
|
|
|
|
Вид зависимости 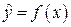 , описывающей опытные данные, выбирает экспериментатор на основе предварительных данных о природе исследуемой зависимости или о расположении эксперимента. Крайне желательно чтобы модель была содержательной, т.е. чтобы входящим в неё постоянным можно было приписать определённый физический смысл. Задача выбора математической модели решается в два этапа:
, описывающей опытные данные, выбирает экспериментатор на основе предварительных данных о природе исследуемой зависимости или о расположении эксперимента. Крайне желательно чтобы модель была содержательной, т.е. чтобы входящим в неё постоянным можно было приписать определённый физический смысл. Задача выбора математической модели решается в два этапа:
1. находят общий вид модели;
2. рассчитывают параметры модели, определяют её конкретный вид.
Если нельзя указать общий вид модели теоретически, то её определяют по форме поля рассеивания экспериментальных точек. Для этого в поле рассеивания помещают графики различных известных функций и находят такие, которые отражают особенности этого поля. Такой выбор неоднозначен, т.к. обычно можно найти несколько подходящих функций.
В некоторых случаях подбор математической модели упрощается, если масштабы по осям  и
и  выбрать так, что график аппроксимирующей функции превратится в прямую линию.
выбрать так, что график аппроксимирующей функции превратится в прямую линию.
Пример:
1) 
Графическое изображение  в координатах
в координатах 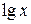 ,
,  является прямой линией с угловым коэффициентом n. По графику можно грубо оценить параметры модели. Для этого проводят линию, берут на ней две точки с координатами
является прямой линией с угловым коэффициентом n. По графику можно грубо оценить параметры модели. Для этого проводят линию, берут на ней две точки с координатами  и
и 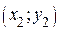 и рассчитывают угловой коэффициент и параметр a:
и рассчитывают угловой коэффициент и параметр a:
 ;
;
2)  - график показательной функции превращается в прямую линию, если выбрать масштаб:
- график показательной функции превращается в прямую линию, если выбрать масштаб: 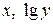 можно приближено оценить параметры a и b.
можно приближено оценить параметры a и b.
Применяя функциональные шкалы, можно использовать рассмотренный метод.
Метод наименьших квадратов
После того как установлен вид математической модели, аналитическими методами рассчитывают её параметры. Наиболее распространен метод наименьших квадратов.
Сущность метода состоит в таком выборе параметров модели, при которых сумма квадратов отклонений  минимальна.
минимальна.
|
|
|
Если систематическая погрешность измерений значений 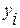 отсутствует, случайная погрешность подчинена гауссовскому закону с постоянной дисперсией, а погрешности последовательности измерений статистически независимы, то вычисленные с помощью метода наименьших квадратов значения параметров математической модели являются оценками максимального правдоподобия.
отсутствует, случайная погрешность подчинена гауссовскому закону с постоянной дисперсией, а погрешности последовательности измерений статистически независимы, то вычисленные с помощью метода наименьших квадратов значения параметров математической модели являются оценками максимального правдоподобия.
При экспериментальной обработке системы двух связанных случайных величин можно пользоваться методом наименьших квадратов. Если предположить, что случайные величины связаны между собой по линейному закону, то метод наименьших квадратов позволяет рассчитать параметры прямой, которая называется линией регрессии.
На практике эти условия выполняются редко, и метод наименьших квадратов является просто удобным аналитическим способом расчета параметров математической модели.
Известно, что прямая линия имеет два параметра. Обозначим их a и b:  .
.
Метод наименьших квадратов позволяет c наилучшей точностью рассчитать коэффициенты А и В.

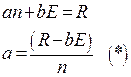




В итоге получим:
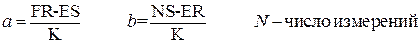 .
.
Порядок выполнения работы
Перед началом работы в окне модели установите время моделирования и шаг в соответствии с вариантом (Simulation->Simulation Parameters->Start time=0, Stop time=10, Solver option->Fixed step, Fixed step size=0.1).
I. Собрать схему (рис. 4.4):

Рис. 4.4
II. Параметры схемы:
Блоки:
1) Simulink->Sourses->Random Number
параметры:
mean 0
variance 1
2) Simulink->Sourses->Ramp
параметры:
slope 1
start time 0
3) Simulink->Math Operators->Sum
4) Simulink->Sinks->To Workspace
параметры:
Variable Name y
Save Format Array
5) Simulink->Sinks->To Workspace1
параметры:
Variable Name x
Save Format Array
Произведите моделирование схемы.
Перейдите в основное меню окна MATLAB.
В окне Command Window наберите имя переменной, указанной в Simulink->Sinks->To Workspace Variable Name, и нажмите enter. Вы увидите результаты.
III. Измените параметры блока Simulink->Sourses->Random Number на
|
|
|
mean 1
variance 1
и измените имена переменных в блоках Simulink->Sinks->To Workspace
например,
Simulink->Sinks->To Workspace
параметры:
Variable Name z
Save Format Array
Simulink->Sinks->To Workspace1
параметры:
Variable Name t
Save Format Array
IV. Произвести моделирование полученной схемы.
Перейдите в основное меню окна MATLAB.
В окне Command Window наберите имя переменной, указанной в Simulink->Sinks->To Workspace Variable Name, и нажмите enter. Вы увидите результаты.
V. По значениям, полученным с выхода сумматора и генератора линейно нарастающего сигнала, построить линию регрессии в следующих осях координат: по оси абсцисс отложить мажорированные значения сигнала с выхода генератора линейно нарастающего сигнала, по оси ординат – соответствующие им значения с выхода сумматора.
VI. Рассчитать коэффициенты теоретической линии регрессии (по формулам) и построить ее в тех же осях координат.
4.4 Контрольные вопросы
1. Что характеризует линия регрессии? Для чего она строится?
2. Каков порядок построения экспериментальной линии регрессии?
3. Каков порядок построения теоретической линии регрессии?
4. Каким будет угол наклона линии регрессии, если две переменные между собой имеют коэффициент корреляции: положительный, равный нулю, отрицательный?
5. В чем суть метода наименьших квадратов?
Лабораторная работа № 5
|
|
|


