 |
Молекулярная физика и термодинамика»
|
|
|
|
ЧОУ ВПО Южно – Уральский институт управления и экономики
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ ПО ДИСЦИПЛИНЕ
«ФИЗИКА»
По направлению:
270800.62 «Строительство»
Челябинск
Физика: Методические рекомендации по выполнению домашней контрольной работы. / О.Р. Шефер - Челябинск: ЧОУ ВПО Южно-Уральский институт управления и экономики, 2011.- 41с.
Физика: Методические рекомендации по выполнению домашней контрольной работы: 270800.62 «Строительство»
Ó Издательство ЧОУ ВПО Южно-Уральский институт управления и экономики», 2011
СОДЕРЖАНИЕ
| Методические рекомендации по выполнению контрольных заданий……. | |
| Задания для домашней контрольной работы……………………………….. | |
| Приложение 1 | |
| Рекомендуемый список литературы………………………………………… |
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ
Контрольная выполняется на листах формата А4, на обложки которой указывается фамилия, имя, отчество, курс, номер группы. Последняя цифра в зачетной книжке определяет номер варианта контрольной работы.
| Первая буква фамилии | номер варианта контрольной работы |
| А, Я, В | |
| Г, С, Е | |
| Ж, З, И | |
| Л, Х | |
| М, Н | |
| О, Р, Ш | |
| Д, Т, У | |
| П, Ф, Ц | |
| Ч, К, Щ | |
| Б, Э, Ю |
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ»
Основные формулы
1.1. Кинематическое уравнение движения материальной точки (центра масс твердого тела) вдоль оси X:

где  - некоторая функция времени.
- некоторая функция времени.
1.2 Средняя путевая скорость

где  - путь, пройденный точкой за интервал времени
- путь, пройденный точкой за интервал времени  . Путь, в отличие от разности координат
. Путь, в отличие от разности координат  , не может убывать и принимать отрицательные значения, т.е.
, не может убывать и принимать отрицательные значения, т.е.  .
.
|
|
|
1.3 Мгновенная скорость
 .
.
1.4 Тангенциальное a τ, нормальное a n и полное a ускорения.

где r - радиус кривизны траектории (в частности, радиус окружности на которой проходит движение).
1.5 Для равноускоренного прямолинейного движения (например, вдоль координат оси X).

где  - проекции на ось X векторов скорости, начальной скорости, ускорения и перемещения.
- проекции на ось X векторов скорости, начальной скорости, ускорения и перемещения.
1.6 Кинетическое уравнение движения материальной точки по окружности

где 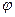 - угол поворота радиус-вектора движущейся точки.
- угол поворота радиус-вектора движущейся точки.
1.7 Угловая скорость  и угловое ускорение
и угловое ускорение 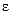
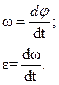
1.8 Для равноускоренного движения по окружности

где  - начальная угловая скорость.
- начальная угловая скорость.
1.9 Взаимосвязь между линейными и угловыми характеристиками движения точки по окружности

1.10 Частота вращения n и число сделанных оборотов N твердого тела

где 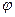 - угол поворота.
- угол поворота.
1.11 Импульс материальной точки, а также тела, движущегося поступательно

где m- масса тела.
1.12 Второй закон Ньютона (основной закон динамики поступательного движения)
 .
.
1.13 Силы, рассматриваемые в механике:
а) сила упругости
 ,
,
где k - жесткость пружины, x - удлинение (укорочение) пружины;
б) сила тяжести
 ,
,
где g - ускорение свободного падения;
в) сила гравитационного взаимодействия
 ,
,
где G - гравитационная постоянная; m1 и m2 - массы взаимодействующих тел, r - расстояние между телами (тела рассматриваются как материальные точки).
г) сила трения (скольжения)
 ,
,
где  - коэффициент трения; N - сила нормального давления.
- коэффициент трения; N - сила нормального давления.
1.14 Закон сохранения импульса

или для двух тел ( )
)

где  и
и  - скорости тел в момент времени, принятый за начальный;
- скорости тел в момент времени, принятый за начальный; 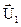 и
и  - скорости тех же тел в момент времени, принятый за конечный.
- скорости тех же тел в момент времени, принятый за конечный.
1.15 Кинетическая энергия тела, движущегося поступательно

1.16 Потенциальная энергия:
а) упруго деформированной пружины

где k - жесткость пружины; x - абсолютная деформация;
|
|
|
б) гравитационных взаимодействий

где G - гравитационная постоянная; m1 и m2 - масса взаимодействующих тел; r - расстояние между ними (тела рассматриваются как материальные точки);
в) тела, находящегося в поле силы тяжести,
 ,
,
где g - ускорение свободного падения; h - высота тела над уровнем принятым за нулевой (формула справедлива при условии A<<R, где R - радиус Земли).
1.17 Закон сохранения механической энергии
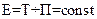 .
.
1.18 Работа, совершаемая внешними силами, определяется как мера изменения энергии системы
 .
.
1.19 Работа, совершаемая силой F на пути от точки 1 до точки 2,
 ,
,
где  - элементарный вектор перемещения;
- элементарный вектор перемещения;  - модуль перемещения; α - угол между силой F и перемещением
- модуль перемещения; α - угол между силой F и перемещением  ;
;  - проекция силы на направление перемещения. При
- проекция силы на направление перемещения. При 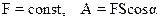 .
.
1.20 Мощность

где F - сила; V - скорость; φ - угол между векторами силы и скорости.
1.21 Момент инерции некоторых тел массой m относительно оси z проходящих через центр масс:
а) стержня длинной l относительно оси, перпендикулярной стержню
 ;
;
б) обруча (тонкостенного цилиндра) радиусом R относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра)
 ;
;
в) диска радиуса R относительно оси, перпендикулярной плоскости диска  .
.
1.22 Момент инерции относительно произвольной оси I равен (теорема Штейнера)
 ,
,
где 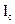 - момент инерции относительно оси, параллельной данной и проходящей через центр масс тела; a - расстояние между осями; m -масса тела.
- момент инерции относительно оси, параллельной данной и проходящей через центр масс тела; a - расстояние между осями; m -масса тела.
1.23 Момент импульса тела, вращающегося относительной неподвижной оси z
 .
.
1.24 Закон сохранения момента импульса системы тел, вращающихся вокруг неподвижной оси:
 ,
,
где  и
и  - моменты инерции системы тел и угловые скорости вращения в моменты времени, принятые за начальный и конечный.
- моменты инерции системы тел и угловые скорости вращения в моменты времени, принятые за начальный и конечный.
1.25 Момент силе F относительно точки O (вращающий момент)
 ,
,
где r - радиус-вектор точки приложения силы.
Модуль вращающего момента
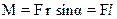
где F - модуль силы; l -плечо силы (длина перпендикуляра, опущенного из точки O на прямую, вдоль которой действует сила).
Момент силы относительно произвольной оси z, проходящей через точку O, является проекцией вращающего момента (т.е. момента силы относительно точки) на эту ось z:
 .
.
 .
.
При Iz=const, Mz=Ize.
|
|
|
1.26 Основной закон динамики вращательного движения относительно неподвижной оси z:
 , при Iz=const, Mz=Ize.
, при Iz=const, Mz=Ize.
1.27 Кинетическая энергия тела, вращающегося вокруг неподвижной оси:
 .
.
1.28 Кинетическая энергия тела при плоско-параллельном движении (состоящем из поступательного и вращательного движения)
 .
.
1.29 Работа, совершаемая внешней силой при вращении твердого тела:
 ,
,
где Mz - момент силы относительно оси вращения z; 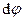 -элементарный угол поворота.
-элементарный угол поворота.
1.30 Мощность при вращении
 ,
,
где  - проекция вектора
- проекция вектора  на направление вектора угловой скорости.
на направление вектора угловой скорости.
1.31 Кинематическое уравнение гармонических колебаний материальной точки:

где x -смешение; A - амплитуда колебаний;  - круговая или циклическая частота;
- круговая или циклическая частота;  - начальная фаза.
- начальная фаза.
1.32 Скорость и ускорение материальной точки совершающей гармонические колебания:
 ;
;
 .
.
1.33 Частота ν, период Т и циклическая частота ω связаны между собой формулами
 .
.
1.34 Квазиупругая сила, действующая при гармонических колебаниях F и коэффициент квазиупругой силы k:
 ,
,
где x - смешение колеблющейся точки; m - её масса;  - циклическая частота.
- циклическая частота.
1.35 Потенциальная П, полная E и кинетическая энергия колеблющейся материальной точки:

где А - амплитуда колебаний.
1.36 Период колебаний математического маятника
 ,
,
где l - длина маятника; g-ускорение свободного падения.
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА»
2.1. Концентрация молекул газа (число молекул в единице объема)
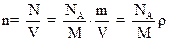 ,
,
где N - число молекул; V – объем; m – масса; М- масса моля; NA - постоянная Авогадро; ρ - плотность газа.
2.2. Количество вещества однородного газа
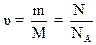 ,
,
где m - масса газа; М – молярная масса газа; N - число молекул газа; NA - постоянная Авогадро; NA = 6,023·1023 моль-1.
2.3. Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа)
 ,
,
где Р – давление; V – объем; R - молярная газовая постоянная, численно равная 8,31 Дж/моль·К; Т- абсолютная температура в кельвинах (Т = t + 273, где t - температура в градусах Цельсия).
2.4. Плотность идеального газа
 .
.
2.5. Объединенный газовый закон (m = const)
|
|
|
 или
или  ,
,
где Р1, V1, T1 - давление, объем, температура газа в начальном состоянии; Р2, V2, T2 - те же величины в конечном состоянии.
2.6. Основное уравнение кинетической теории газов
 ,
,
где <εп>- средняя кинетическая энергия поступательного движения молекулы; n - концентрация молекул (число молекул в единице объёма).
2.7. Средняя полная кинетическая энергия молекулы:
 ,
,
где i - число степеней свободы; k - постоянная Больцмана (k =R/NA).
2.8. Молярные теплоемкости газа при постоянном объёме (CV) и при постоянном давлении (СP)
 ;
;  .
.
2.9. Внутренняя энергия идеального газа
 .
.
2.10. Первое начало термодинамики
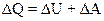 ,
,
где ∆Q - теплота, сообщенная газу; ∆U - изменение внутренней энергии газа; ∆А - работа, совершенная газом против внешних сил.
2.10. Работа расширения газа:
 - при изобарном процессе;
- при изобарном процессе;
 - при изотермическом процессе;
- при изотермическом процессе;
 при адиабатном процессе.
при адиабатном процессе.
2.11. Уравнение Пуассона (уравнение адиабаты)
 ,
,
где 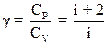 .
.
2.12. Термический коэффициент полезного действия цикла Карно
 ,
,
где Q1 - теплота, полученная рабочим телом от теплоотдатчика; Q2 – теплота, переданная рабочим телом теплоприемнику; T1 и T2 -термодинамические температуры теплоотдатчика и теплоприемника соответственно.
|
|
|


