Главная | Обратная связь | Поможем написать вашу работу!

Задания для самостоятельной работы

Оглавление

Рекомендации к выполнению контрольной работы.. 3

Тема № 1. Перевод чисел из одной системы счисления в другую.. 3

Задания для самостоятельной работы.. 6

Тема № 2. Двоичная арифметика. 8

Задания для самостоятельной работы.. 9

Тема № 3. Решение задач средствами электронных таблиц MS Excel. 10

Задача 1. 10

Задача 2. 13

Задача 3. 15

Приложение 1. 17

Рекомендации к выполнению контрольной работы

В данной контрольной работе содержатся задания по слеующим темам: «Системы счисления», «Двоичная арифметика», «Решение задач средствами электронных таблиц MS Excel». В данном документе каждая тема содержит следующие разделы:

- основные понятия

- примеры решения задач

- варианты заданий для самостоятельного выполнения.

Студент должен выполнить контрольную работу в соответствии со своим индивидуальным вариантом, - шифром, определяемым как сумма двух последних цифр номера зачетной книжки. Работа выполняется и предоставляется в электронном виде, титульный лист, подписанный студентом, сдается в бумажном виде. Образец титульного листа приведен в приложении 1.

Файл с контрольной работой должен быть назван следующим образом:

№зачетной книжки_с-НТСз11_2017_7

Например:120075_ с-НТСз11_2017_7

Тема № 1. Перевод чисел из одной системы счисления в другую

Основные понятия. Количество различных цифр p, используемых в позиционной системе, определяет название системы счисления и называется основанием р- ной системы счисления.

Любое число N в позиционной системе счисления с основанием р может быть представлено в виде полинома от основания р:

N=a_kp^k+a_k_-1p^k^-1+…+a₁p¹+a₀p⁰+a_-1p^-1+a_-2p^-2+…, где N-число, a_i – цифры числа

(коэффициенты при степенях p), p – основание системы счисления (p>1).

Числа записывают в виде последовательности цифр:

N=a_ka_k_-1…a₁a₀.a_-1a_-2… - точка в последовательности отделяет целую часть от дробной. Точка опускается, если число целое.

В компьютерных системах применяют позиционные системы счисления с недесятичным основанием – двоичную, восьмеричную, шестнадцатеричную. В аппаратной основе ЭВМ лежат двухпозиционные элементы, которые могут находиться только в двух состояниях, одно из которых обозначается 0, а другое 1. Поэтому арифметическо-логической основой ЭВМ является двоичная система счисления.

В двоичной системе счисления используется две цифры – 0 и 1. В общем виде число в двоичной системе счисления представляется в форме:

X = a_n*2ⁿ + a_n-1*2^n-1+... + a₁ *2¹ + a₀ *2⁰+a_-12^-1+a_-22^-2+… a_i принадлежат 0,1

Для более удобного представления двоичных данных также используется система счисления с основанием восемь (восьмеричная система счисления). В восьмеричной системе счисления используется восемь цифр: 0,1,2,3,4,5,6,7. Для представления одной цифры восьмеричной системы используется три двоичных разряда.

Для "стенографического" представления двоичных чисел используется система счисления с основанием 16 (шестнадцатеричная система счисления). В шестнадцатеричной системе счисления используется шестнадцать цифр: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Для представления одной цифры шестнадцатеричной системы используется четыре двоичных разряда.

Таблица. Соответствие чисел, записанных в различных системах счисления

Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная









			A
			B
			C
			D
			E
			F

Примеры

Перевод из двоичной, восьмеричной и шестнадцатеричной в десятичную систему счисления

a. перевести 10101101,101₂в десятичную систему счисления

10101101,101₂=1×2⁷+0×2⁶+1×2⁵+0×2⁴+1×2³+1×2²+0×2¹+1×2⁰+1×2^-1+0×2^-2+1×2^-3=173,625₁₀

b. перевести 53,2₈ в десятичную систему счисления

53,2₈=5×8¹+3×8⁰+2×8^-1=43,25

c. перевести 23Е,2₁₆ в десятичную систему счисления

23Е,2₁₆=2×16²+3×16¹+14×16⁰+2×16^-1= 574,125

Перевод из десятичной системы в двоичную, восьмеричную и шестнадцатеричную системы счисления.

перевести 124₁₀ в двоичную систему

Ответ: 124₁₀=1111100₂

b. перевести 124₁₀ в восьмеричную систему

Ответ: 124₁₀=174₈

3. Перевод правильных дробей из десятичной системы в двоичную, восьмеричную и шестнадцатеричную системы счисления.

Перевести число 0,65625₁₀ в восьмеричную систему счисления.

Ответ: 0,65625₁₀ = 0,52₈

Перевести число 0,65625₁₀ в шестнадцатеричную систему счисления.

Ответ: 0,65625₁₀ = 0,A8₁₆

Замечание: при переводе смешанных чисел целые и дробные части переводятся отдельно.

4. Перевод чисел из восьмеричной и шестнадцатеричной систем в двоичную.

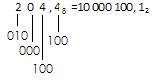перевести в двоичную систему число 204,4₈

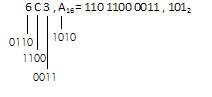перевести в двоичную систему число 6С3,А₁₆

5. Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную.

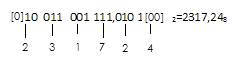перевести в восьмеричную систему число 10011001111,0101₂

перевести в шестнадцатеричную систему число 10111111011,100011₂

Задания для самостоятельной работы

Вариант	Переведите в десятичную систему	Переведите десятичные числа в 2-ю, 8-ю и 16-ю системы счисления	8-ричное число переведите в 16-ричное и наоборот
	10100101111,101₂ 2451,23₈ 2BA,D3₁₆	286,06	2451,23₈ 2BA,D3₁₆
	11100100111,1101₂ 7351,33₈ 8CA,A3₁₆	234,5	7351,33₈ 8CA,A3₁₆
	10000100100,01₂ 3512,31₈ 9B1,A4₁₆	431,6	3512,31₈ 9B1,A4₁₆
	10001111111,101₂ 1234,56₈ 123,D3₁₆	806,1	1234,56₈ 123,D3₁₆
	11000000101,1001₂ 1574,61₈ 35C,F1₁₆	372,1	1574,61₈ 35C,F1₁₆
	11100011100,001₂ 1523,24₈ 1AF,73₁₆	910,8	1523,24₈ 1AF,73₁₆
	10010011100,0101₂ 7243,12₈ 13A,1C₁₆	142,4	7243,12₈ 13A,1C₁₆
	1001100110100,1101₂ 6432,21₈ 5AD,4D₁₆	581,4	6432,21₈ 5AD,4D₁₆
	10011111100,001₂ 1723,24₈ 1AC,D3₁₆	132,4	1723,24₈ 1AC,D3₁₆
	11111110000,0101₂ 1723,24₈ 1AC,D3₁₆	867,2	1723,24₈ 1AC,D3₁₆
	10000111111,011₂ 1072,02₈ 2AC,F3₁₆	211,6	1072,02₈ 2AC,F3₁₆
	10000101011,011₂ 6052,03₈ 4A1,23₁₆	432,5	6052,03₈ 4A1,23₁₆
	10111101011,011₂ 3152,04₈ 9A3,13₁₆	621,5	3152,04₈ 9A3,13₁₆
	11010101010,011₂ 1131,76₈ 9B1,A1₁₆	876,3	1131,76₈ 9B1,A1₁₆
	11000100011,001₂ 3431,44₈ 981,21₁₆	600,9	3431,44₈ 981,21₁₆
	10000101011,1001₂ 3654,11₈ 2B7,E1₁₆	905,7	3654,11₈ 2B7,E1₁₆
	10110101011,1011₂ 6123,51₈ 357,B1₁₆	660,7	6123,51₈ 357,B1₁₆
	10110111001,01₂ 1467,23₈ 3CA,7B₁₆	543,9	1467,23₈ 3CA,7B₁₆
	100010111001,01₂ 6714,77₈ 3CB,7A₁₆	654,7	6714,77₈ 3CB,7A₁₆
	110101011001,01₂ 3067,07₈ 1CD,4A₁₆	146,3	3067,07₈ 1CD,4A₁₆
	111111011001,01₂ 4356,11₈ 8AD,4A₁₆	678,4	4356,11₈ 8AD,4A₁₆
	111000011001,01₂ 1272,13₈ 30A,33₁₆	703,2	1272,13₈ 30A,33₁₆
	111000000011,01₂ 4352,71₈ 31B,41₁₆	456,8	4352,71₈ 31B,41₁₆
	100010001111,01₂ 1622,32₈ 34C,04₁₆	118,5	1622,32₈ 34C,04₁₆
	101110001111,01₂ 7611,53₈ 78F,AA₁₆	578,2	7611,53₈ 78F,AA₁₆

12	Поделиться:

Воспользуйтесь поиском по сайту: