Многокритериальная многомерная задача о ранце

D – мерная задача о ранце с n предметами и m аддитивными критериями:

(9)

(10)

(11)

0≤a_ij≤b_i Задачу (9)-(11) обозначим символом Z.

Для получения полной совокупности эффективных в рассматриваемой задаче оценок E(Z) рассмотрим совокупность задач Z(K,p):

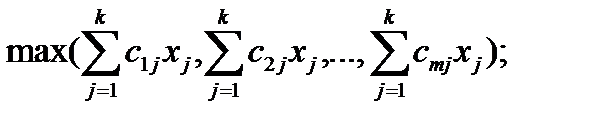(12)

(13)

(14)

, где k ∈{1,2,...,n}, p ∈P; здесь и далее P - множество всех целочисленных векторов

(p ₁ ,p₂ ,…, p_d)- с координатами, удовлетворяющими условиям 0 ≤ p_i ≤ b_i, .

Полную совокупность эффективных оценок в задаче Z(k, p) обозначим

E(k, p). При этом E(Z) =E(n, b), здесь b= (b₁,b₂,…,b_d).

(0,0,…,0) если ∃ i: 0≤p_i<a_il;

Е(1, р)=.

(c₁₁,c₂₁,…,c_m1) при a_il≤p_i для всех

Условимся далее обозначать через С_j и a_j векторы (с_1j,с_2j,…, с_mj) и (a_1j,a_2j,…, a_dj).

Пусть уже найдены значения E(k, p) для некоторого k и всех возможных p

из P. Тогда значения E(k +1, p) вычисляются по формуле

Е(k, р), если ∃ i: 0≤p_i<a_ik+1;

Е(k+1, р)= eff (Е(k, р)∪{C_k+1)⊕E(k, p -a_k+1)})

. при а_ik+1≤p_i для всех

 

здесь k = 1,2,...,n −1; p ∈ P.

Действительно, задача Z(k+1, p) отличается от Z(k, p) дополнительным

наличием булевозначной переменной х_k+1. В случае ∃ i: 0≤p_i<a_ik+1 имеем

E(k+1, p) =E(k, p), так как допустимым оказывается только нулевое значение данной переменной.

Если же для всех имеет место а_ik+1≤p_i, то для переменной х_k+1 следует

рассмотреть две возможности: х_k+1= 0 и х_k+1= 1.

Решение задачи Z сводится к последовательному заполнению строк таблицы. Заголовками строк являются допустимые значения первого аргумента функции E(k, p) r, т.е. натуральные числа от 1 до n. Заголовками столбцов являются допустимые значения второго аргумента. Указанные векторы перечисляются как заголовки столбцов в лексикографическом порядке. В каждую клетку (k, p) таблицы вносится множество векторов E(k, p). Процесс решения задачи Z заканчивается нахождением множества E(Z) =E(n, b)

 

Постановка многокритериальной задачи

Сформулируем бикритериальную задачу о грузоперевозках. Первым максимизированным критерием у нас по-прежнему будет выступать возможная прибыль с продажи товара в тысячах условных единиц. Вторым максимизируемым критерием у нас будет выступать степень его спроса у потребителя (в таком случае помимо получения прибыли мы сэкономим время, которое могли бы потерять, погрузив не ходовой товар). Вес товара и максимальная грузоподъемность судна указаны в десятках тонн.

Найдя оптимальное решение для поставленной задачи, определим, какие товары выгоднее погрузить, с целью максимальной выгоды от пордажи товара в минимальные сроки..

3х₁+х₂+2х₃+5х₄+4х₅àmax - прибыль от товара

х₁+3х₂+3х₃+х₄+5х₅àmax - степень спроса у потребителя

2х₁+х₂+х₃+4х₄+3х₅ ≤ 10 - вес товара и максимальная грузоподъемность

x_i {0.1}, i= судна

		(3,1)1	(3,1)1	(3,1)1	(3,1)1	(3,1)1	(3,1)1	(3,1)1	(3,1)1	(3,1)1
	(1,3)2	(3,1)1 (1,3)2	(4,4)1,2	(4,4)1,2	(4,4)1,2	(4,4)1,2	(4,4)1,2	(4,4)1,2	(4,4)1,2	(4,4)1,2
	(2,3)3	(3,6)2,3	(5,4)1,3 (3,6)2,3	(6,7)1,2,3	(6,7)1,2,3	(6,7)1,2,3	(6,7)1,2,3	(6,7)1,2,3	(6,7)1,2,3	(6,7)1,2,3
	(2,3)3	(3,6)2,3	(5,4)1,3 (3,6)2,3	(6,7)1,2,3	(6,7)1,2,3 (7,4) 3,4	(8,7)2,3,4	(10,5)1,3,4 (8,7)2,3,4	(11,8)1,2,3,4	(11,8)1,2,3,4	(11,8)1,2,3,4
	(2,3)3	(3,6)2,3	(5,4)1,3 (3,6)2,3 (4,5)5	(6,8)3,5	(7,11)1,3,5	(9,9)1,3,5 (7,11)1,3,5	(10,12)1,2,3,5	(10,12)1,2,3,5 (11,9)3,4,5	(12,12)2,3,4,5	(14,10)1,3,4,5 (12,12)2,3,4,5

 

Построена таблица включающая в себя полную совокупность эффективных оценок Е. В итоге мы получили две самых эффективных оценки (14,10) и (12,12). ЛПР необходимо выбрать одну из них. Руководствуясь соображениями, что все – таки прибыль нам несколько важнее, чем быстрый сбыт товара, ЛПР выбирает оценку (14,10).

Поскольку К_opt=(14,10), то Парето- оптимальное решение выглядит: х₁=х₃=х₄=х₅=1 _, х₂=0;

Следовательно погружены все предметы кроме второго с учетом их стоимости и приоритету у потребителей. И от их продажи товаров мы получим прибыль 14тыс.у.е.

 

Заключение

Мы ознакомились с принципами постановки и методами решения задач дискретной оптимизации, возникающих в процессах управления и принятия решений в системах управления.

В курсовой работе в качестве основной задачи дискретной оптимизации рассмотрены задачи о ранце на примере задачи о водных грузоперевозках.

Приведены в качестве иллюстрированного примера алгоритмы решения однокритериальной и многокритериальной задачи о ранце.

Дополнительно описываются различные методы решения многокритериальных задач, базирующихся на концепции эффективной оценки и Парето-оптимального решения, и так же рассмотрен подход, использующий схемы компромисса.

 

Список литературы

1. Д.И.Коган Методы оптимизации. Типовые алгоритмы решения задач дискретной оптимизации. Учебное пособие. Москва, МГУПИ, 2009

2. Д.И.Коган Многокритериальные задачи принятия решений в системах управления. Москва, МГУПИ, 2008

3. Д.И. Коган Лекции по предмету “теория систем”

4. http://xreferat.ru/33/6244-1-metody-resheniya-zadachi-o-ryukzake.html

5. http://www.dissercat.com/content/mnogokriterialnye-zadachi-rantsevogo-tipa-matematicheskie-modeli-i-algoritmy-resheniya

6. http://andreyusoft.narod.ru/uchebnik1/part2p3.html

 

 

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: