 |
Непрерывные случайные величины. Функция и плотность распределения.
|
|
|
|
Вопросы по теории вероятностей
- + Теорема о повторении опытов.
Ответ на билет 1
+ Основные понятия теории вероятностей: события, вероятность события, частота события, случайная величина.
X – случайная величина.
x – значение случайной величины.
- непрерывная случайная величина
Дискретная случайная величина – можно пересчитать.
Практически не возможное событие, вероятность которого близка к нулю 0 (0,01; 0,1).
Практически достоверное событие, вероятность которого близка к единице 1 (0,99; 0,9888).
Ответ на билет 2
Сумма и произведение событий, теоремы сложения и умножения вероятностей.
Сумма событий и произведение событий.
А,В,….,G - события
Суммой событий называется некоторое событие S=A+B+….+G=A 
B …. G, состоящее в появлении хотя бы одного из этих событий.
Пример: Допустим идет стрельба по мишени
А 1 - попадание при первом выстреле
А 2 - попадание при втором выстреле
S=A 1 +A 2 (хотя бы одно попадание)
Произведением некоторых событий называется событие, состоящее в совместном появлении всех этих событий. S=ABC…G=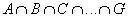 
Пример: А 1 - промах при первом выстреле
А 2 - промах при втором выстреле
А 3 - промах при третьем выстреле
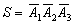(не одного попадания)
Теорема сложения вероятностей.
Вероятность двух не совместных событий равна сумме вероятностей этих событий.
P(A) P(B)
P(A+B)=P(A)+P(B)
S=S 1 +S 2 +…+S n
P(S)=P(S 1 )+P(S 2 )+…+P(S n )
Следствие: Если событие S 1 , S 2 , …, S n образуют полную группу не совместных событий, то сумма их вероятностей равна 1.
Противоположными событиями называются два не совместных события, образующие полную группу
. 
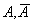(пример - монетка имеющая орел и орешко)
Если два события A и B совместны, то вероятность совместного появления двух событий вычисляется по формуле: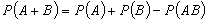 
|
|
|
Условие независимости события А от события В: P(A|B)=P(A), то P(B|A)=P(B)
Условие зависимости события А от события В: P(A|B)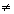 
P(A), P(B|A) 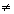P(B) (Если А не зависит от В, то и В не зависит от А - условие не зависимости условий взаимно).
Вероятность произведения двух событий равна произведению вероятности одного из событий на условную вероятность другого, вычисленную при условии, что событие первое имело место:
P(AB)=P(A)P(B|A), P(AB)=P(B)P(A|B)
Следствие: Вероятность произведения нескольких не зависимых событий равна произведению вероятностей этих событий. P(A 1 A 2 …A n )=P(A 1 )P(A 2 )…P(A n )
Пример: на монете выпадет орел 2 раза
S=A ор A ор S=P 2 (A)=(1/2) 2 =1/4
Ответ на билет 3
Дискретные случайные величины. Ряд, многоугольник и функция распределения.
Закон распределения случайных величин
Ряд и многоугольник распределений. Случайная величина - это величина, которая в результате опыта может принять то или иное значение не известное заранее какое.
Большие буквы - случайные величины. Малые буквы - их возможные решения.
Рассмотрим случайную дискретную величину Х с возможными значениями x 1 , x 2 , …, x n
В результате опыта: 
Обозначим вероятность соответствующих событий через P i
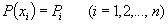, так как рассматриваемые события образуют полную группу не совместных событий, то 
Х полностью описана с вероятностной точки зрения, если мы зададим распределение вероятности p i (i=1,2…,n), то есть в точности указаны решения вероятности p i каждого события x i
Этим будет установлен закон случайной величины x i.
Законом распределения случайной величины называется всякое соотношение устанавливающее связь между возможными значениями случайных величин и соответствующими вероятностями.
Простейшей формой записи законов распределения является таблица:
| X | x1, x2, …, xn |
| P | p1, p2, …, pn |
Многоугольник и ряд распределения полностью характеризует случайную величину и является одной из форм законов распределения. (Для непрерывной случайной величины построить невозможно).
|
|
|
Ответ на билет 4
Непрерывные случайные величины. Функция и плотность распределения.
Плотность и функция распределения.
Функция распределения непрерывной случайной величины (Х), задана выражением:
a. Найти коэффициент а
b. Найти плотность распределения F(x)
c. Найти вероятность попадания случайной величины на участок P(0,5<x<3)=?
d. Построить график функций
F(4)=1 -> a4=1, a=0,25
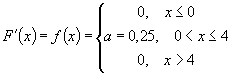
- два способа решения.
Ответ на билет 5
Функция распределения; квантиль и а -процентная точка распределения.
Функция распределения
Для непрерывной случайной величины Х вместо вероятности равенства Х=х используют вероятность Р(Х<х). F(x)=P(X<x)
F-функция распределения случайной величины х
F(x) -интегральный закон распределения или интегральная функция распределения.
F(x) -самая универсальная характеристика случайной величины, она существует для всех случайных величин как дискретных так и непрерывных.
|
|
|
