 |
Основные свойства функции распределения.
|
|
|
|
1. Функция распределения F(x) есть не убывающая функция своего аргумента, т.е. при x 2 >x 1 F(x 2 )>=F(x 1 )
2. При 
функция распределения F(x)=0; F(
)=0
- При
F(x)=1; F(
)=1
Для дискретной случайной величины: 
Функция распределения любой дискретной случайной
величины всегда есть разрывная ступенчатая функция,
скачки которых происходят в точках соответствующих
возможных значений случайных величин и равны
вероятностям этих значений. Сумма всех скачков
равна 1.
F(x) непрерывной случайной величины
Часто используют величины квантиль 
и 
-процентная точка 
Квантиль - решение уравнения 
- процентная точка определяется из уравнения 
Ответ на билет 6
+ Формула полной вероятности и теорема гипотез.
Формула полной вероятности.
Пусть требуется определить вероятность некоторого события А, которое может произойти вместе с одним из событий H 1 , H 2 , …, H n, образующие полную группу не совместных событий. Эти события назовем гипотезами. Докажем, что в этом случае вероятность событий:
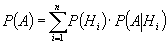
Вероятность события А вычисляется как сумма произведений вероятностей каждой гипотезы на условную вероятность события при этой гипотезе.
применяем 2 е теоремы:
Теорема гипотез (формула Байеса).
Пусть вероятность полной группы не совместных гипотез H 1 , H 2 , …, H n известны и равны P(H 1 ), P(H 2 ), …, P(H n). Событие А может появиться совместно с условной вероятностью P(A|H i) (i=1,2,…,n).
Спрашивается, как следует изменить вероятности гипотез после проведения опытов в связи с появлением этого события. Иными словами, требуется найти условную вероятность P(H i,A).
Формула Байеса: 
Ответ на билет 7
+ Числовые характеристики случайных величин: моменты; дисперсия; и среднеквадратичное отклонение.
|
|
|
Числовые характеристики случайных величин.
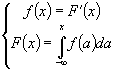Закон распределения случайных величин, представленный в той или иной форме, дает исчерпывающее описание случайной величины. Наиболее существенные особенности распределения в компактной форме описываются так называемыми числовыми характеристиками случайных величин. Они играют в теории вероятности огромную роль, с их помощью облегчается решение вероятностных задач. Рассмотрим наиболее часто встречающиеся числовые характеристики.
Характеристики положения.
Мат. Ожидание Мода Медиана
Важнейшая характеристика математическое ожидание, которая показывает среднее значение случайной величины.
Математическое ожидание величины Х обозначается М[X], или m x.
Для дискретных случайных величин математическое ожидание:
Сумма значений соответствующего значения на вероятность случайных величин.
Модой (Mod) случайной величины Х называют ее наиболее вероятное значение.
Для дискретной случайной величины. Для непрерывной случайной величины.
Mod=X 3 Mod=X 0
Одно-модальное распределение
Много модальное распределение
В общем случае Mod и математическое ожидание не совпадают.
Медианой (Med) случайной величины Х называют такое значение, для которой вероятность того что P(X<Med)=P(X>Med). У любого распределения Med может быть только один.
Med разделяет площадь под кривой на 2 равные части. В случае одно-модального и симметричного распределения mx=Mod=Med
Моменты.
Чаще всего на практике применяются моменты двух видов начальное и центральное.
Начальный момент. 
-го порядка дискретной случайной величины Х называется сумма вида:
Для непрерывной случайной величины Х начальным моментом порядка называется интеграл 
, очевидно, что математическое ожидание случайной величины есть первый начальный момент. 
Пользуясь знаком (оператором) М, начальный момент -го порядка можно представить как мат. ожидание -ой степени некоторой случайной величины.
|
|
|
Центрированной случайной величиной соответственной случайной величины Х называют отклонение случайной величины Х от ее математического ожидания:
Математическое ожидание центрированной случайной величины равно 0.
Для дискретных случайных величин имеем:
Моменты центрированной случайной величины носят название Центральных моментов
Центральный момент порядка случайной величины Х называют математическим ожиданием -ой степени соответствующей центрированной случайной величины.
Для дискретных случайных величин:
Для непрерывных случайных величин:
|
|
|
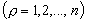
