 |
Приведение СЛАУ к виду, удобному для итераций.
|
|
|
|
ЗАДАНИЕ №1
ПРИБЛИЖЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
(решение трансцендентных и алгебраических уравнений)
Характеристическое уравнение системы автоматического управления (САУ) режимами работы электрических систем в общем случае имеет нелинейный вид. Решаются такие уравнения, как правило, численными методами.
В задании №1 необходимо решить два нелинейных уравнения (трансцендентное и алгебраическое).
Порядок расчета:
1. Графически отделить корни.
2. Уточнить корни уравнений численными методами согласно варианту задания (по одному корню для каждого уравнения).
3. Проверить решение трансцендентного уравнения при помощи встроенного в MathCAD блока решений Given-Minerr, арешение алгебраического уравнения – встроенной в MathCAD функцией polyroots().
Указания к выполнению задания
Для графического отделения корней в MathCAD строится график функции  , составленной на основе исходного уравнения.
, составленной на основе исходного уравнения.
Например, дано трансцендентное уравнение:
 .
.
Для составления функции переносим все слагаемые в правую часть, получим:
 .
.
Отделение корней состоит в определении интервалов [a,b], в котором график функции  один раз пересекает ось абсцисс (интервалы изоляции корня).
один раз пересекает ось абсцисс (интервалы изоляции корня).
Алгоритмы методов уточнения корней.
Метод половинного деления.
1) Исходные данные: интервал [a,b], заданная погрешность расчета 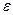 . Для этого и последующих заданий можно принять
. Для этого и последующих заданий можно принять  .
.
2) Рассчитать:  .
.
3) Приближенное значение корня:
 . (*)
. (*)
4) Рассчитать  .
.
5) Если  или
или  , то
, то  - корень, полученный с заданной точностью (окончание расчета).
- корень, полученный с заданной точностью (окончание расчета).
Если нет, то:
при 
 и переход к (*);
и переход к (*);
при 
 ,
,  и переход к (*).
и переход к (*).
Метод хорд.
1) Исходные данные: интервал [a,b], заданная погрешность расчета 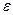 .
.
|
|
|
2) Определить первую и вторую производные функции  -
-  и
и  .
.
3) Рассчитать: 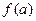 ,
, 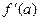 ,
,  ;
;
 ,
,  ,
, 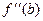 .
.
4) Определить дополнительные величины  ,
,  и
и  :
:
 - минимальное значение из
- минимальное значение из 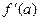 и
и  ;
;
если 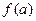 и
и  имеют одинаковый знак, то
имеют одинаковый знак, то  ,
,  ,
,
иначе  ,
,  .
.
5) Рассчитать:  ,
,  .
.
6) Приближенное значение корня:
 . (*)
. (*)
7) Рассчитать  .
.
Если  , то
, то  - корень, полученный с заданной точностью (окончание расчета).
- корень, полученный с заданной точностью (окончание расчета).
Если нет, то:  ,
,  и переход к (*).
и переход к (*).
Метод касательных.
1) Исходные данные: интервал [a,b], заданная погрешность расчета 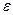 .
.
2) Определить первую и вторую производные функции  -
-  и
и  .
.
3) Рассчитать: 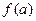 ,
, 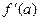 ,
,  ;
;
 ,
,  ,
, 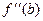 .
.
4) Определить дополнительные величины  ,
,  и
и  :
:
 - минимальное значение из
- минимальное значение из 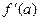 и
и  ;
;
 - максимальное значение из
- максимальное значение из  и
и 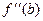 ;
;
если 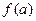 и
и  имеют одинаковый знак, то
имеют одинаковый знак, то  , иначе
, иначе  .
.
5) Приближенное значение корня:
 . (*)
. (*)
6) Если  , то
, то  - корень, полученный с заданной точностью (окончание расчета). Если нет, то:
- корень, полученный с заданной точностью (окончание расчета). Если нет, то:  и переход к (*).
и переход к (*).
ЗАДАНИЕ №2
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ)
В результате применения законов Кирхгофа к расчету электрических цепей постоянного тока получают систему линейных алгебраических уравнений, которая связывает между собой параметры цепи и параметры режима.
Решают СЛАУ различными методами, в частности – итерационными.
В задании №2 необходимо решить систему линейных алгебраических уравнений методом ускоренной итерации (метод Зейделя).
Порядок расчета:
1. Привести СЛАУ к виду, удобному для итераций.
2. Преобразованную (эквивалентную) систему привести к нормальному виду.
3. Принять за начальные приближения свободные члены нормализованных уравнений системы.
4. Решить СЛАУ (согласно варианту задания) с точностью  .
.
5. Проверить решение СЛАУ при помощи встроенной в MathCAD функции lsolve().
Указания к выполнению задания
Приведение СЛАУ к виду, удобному для итераций.
Для обеспечения сходимости итерационного процесса достаточно, чтобы для исходной системы модули диагональных коэффициентов каждого уравнения были больше суммы модулей всех остальных коэффициентов в этом же уравнении. Приведение исходной системы к эквивалентной, для которой выполняются условия сходимости, делается с помощью элементарных преобразований.
|
|
|
Например, для системы из трех уравнений:
 .
.
Если  ,
,  и
и  - сходимость итерационного процесса обеспечена.
- сходимость итерационного процесса обеспечена.
Пример.
Привести к виду, удобному для итераций, систему:

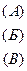 .
.
Просматриваем уравнения: в уравнении (Б)  - следовательно, принимаем уравнение (Б) в качестве второго уравнения эквивалентной системы.
- следовательно, принимаем уравнение (Б) в качестве второго уравнения эквивалентной системы.
В уравнении (А)  - принимаем уравнение (А) в качестве третьего уравнения исходной системы.
- принимаем уравнение (А) в качестве третьего уравнения исходной системы.
За первое уравнение эквивалентной системы примем комбинацию (2·В+А), тогда получим:
 ,
,
 .
.
В итоге получаем эквивалентную систему уравнений, удобную для итераций:
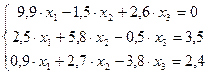 .
.
|
|
|


