 |
Указания к выполнению задания
|
|
|
|
Аппроксимация – это нахождение достаточно простого вида функции 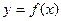 , значения которой при
, значения которой при  мало отличались бы от исходных табличных данных. Аппроксимация функции состоит из двух этапов:
мало отличались бы от исходных табличных данных. Аппроксимация функции состоит из двух этапов:
1) выбор общего вида функции;
2) определение наилучших параметров выбранной функции,
Рассмотрим, как осуществляется подбор вида аппроксимирующей функции для простейших нелинейных зависимостей.
Пусть  есть функция одной переменной
есть функция одной переменной  с двумя параметрами
с двумя параметрами  и
и  . В качестве набора функций, из которых будем выбирать эмпирическую зависимость (аппроксимирующую функцию), рассмотрим:
. В качестве набора функций, из которых будем выбирать эмпирическую зависимость (аппроксимирующую функцию), рассмотрим:
1) линейную функцию  ;
;
2) показательную функцию  ;
;
3) дробно-рациональную функцию  ;
;
4) логарифмическую функцию  ;
;
5) степенную функцию  ;
;
6) гиперболическую функцию  ;
;
7) дробно-рациональную функцию вида  .
.
Для выбора вида аналитической зависимости  выполнят следующие этапы:
выполнят следующие этапы:
- исходную таблицу данных представляют в виде графика 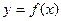 ;
;
- на заданном отрезке изменения  выбирают две точки, достаточно надежные и, по возможности, далеко отстоящие друг от друга, например,
выбирают две точки, достаточно надежные и, по возможности, далеко отстоящие друг от друга, например,  и
и  ;
;
- вычисляют:
среднее арифметическое  ;
;
среднее геометрическое 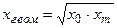 ;
;
среднее гармоническое  ;
;
- по вычисленным значениям  , пользуясь графиком
, пользуясь графиком 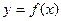 , находят значения
, находят значения  :
:
 ,
,  ,
,  ;
;
- вычисляют:
 ;
;  ;
;  ;
;
- сравнивают найденные из графика  с вычисленными
с вычисленными  и оценивают следующие погрешности результата сравнения:
и оценивают следующие погрешности результата сравнения:
 ;
;  ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
- находят из этих погрешностей минимальную: 
и делают заключение о виде аппроксимирующей функции. Например, если  , то вид функции – четвертый в приведенном выше наборе функций;
, то вид функции – четвертый в приведенном выше наборе функций;
- выполняют проверку правильности выбранного вида функции с помощью метода выравнивания.
Суть метода заключается в следующем: предполагая, что между  и
и  существует зависимость определенного вида, находят некоторые величины
существует зависимость определенного вида, находят некоторые величины  и
и  , которые при сделанном предположении связаны линейной зависимостью. Например, если
, которые при сделанном предположении связаны линейной зависимостью. Например, если  , то берут
, то берут  ,
,  или
или  и
и  . Вычисляя для заданных значений
. Вычисляя для заданных значений  и
и  соответствующие значения
соответствующие значения  и
и  и изображая зависимость
и изображая зависимость  графически, легко увидеть, близка ли последняя к линейной. Если точки зависимости
графически, легко увидеть, близка ли последняя к линейной. Если точки зависимости  лежат на одной прямой, выбранная функция
лежат на одной прямой, выбранная функция 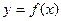 является подходящей.
является подходящей.
|
|
|
Для приведенных выше нелинейных зависимостей можно получить следующие линейные зависимости:
2)  , где
, где  ,
,  ,
, 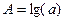 ,
,  ;
;
3)  , где
, где  ,
,  ;
;
4)  , где
, где  ,
,  ;
;
5)  , где
, где  ,
,  ,
, 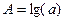 ;
;
6)  , где
, где  ,
,  ;
;
7)  , где
, где  ,
,  .
.
Уточнение параметров  и
и  для функции вида
для функции вида  можно выполнить по методу выбранных точек.
можно выполнить по методу выбранных точек.
Для этого на построенной кривой (или прямой в методе выравнивания) берут две произвольные точки  и
и  , составляют систему
, составляют систему
 ,
,
разрешают ее относительно параметров  и
и  и подставляют полученные значения в формулу аппроксимирующей функции.
и подставляют полученные значения в формулу аппроксимирующей функции.
ЗАДАНИЕ №5
РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
(одношаговые методы решения дифференциальных уравнений)
Расчет переходных процессов в электрических цепях связан с решением дифференциальных уравнений, составленным на основе законов коммутации и законов Кирхгофа для мгновенных значений напряжений и токов.
Наиболее часто в электротехнике дифференциальные уравнения решаются численными методами (Эйлера, Эйлера-Коши и Рунге-Кутта 4-го порядка).
В задании №5 необходимо решить дифференциальное уравнение вышеуказанными методами.
Порядок выполнения задания:
1. Решить дифференциальное уравнение (согласно варианту задания) на заданном отрезке изменения аргумента с заданными начальными условиями и шагом расчета.
2. Проверить решение дифференциального уравнения при помощи встроенных в MathCAD функций rkfixed() или Rkadapt().
|
|
|


