 |
Теплопроводность. Уравнение теплопроводности
|
|
|
|
Теплопроводность - это один из видов теплопередачи. Передача тепла может осуществляться с помощью различных механизмов.
Все тела излучают электромагнитные волны. При комнатной температуре это в основном излучение инфракрасного диапазона. Так происходит лучистый теплообмен.
При наличии поля тяжести еще одним механизмом теплопередачи в текучих средах может служить конвекция. Если к сосуду, содержащему жидкость или газ, тепло подводится через днище, в первую очередь прогреваются нижние порции вещества, их плотность уменьшается, они всплывают вверх и отдают часть полученного тепла верхним слоям.
При теплопроводности перенос энергии осуществляется в результате непосредственной передачи энергии от частиц (молекул, атомов, электронов), обладающих большей энергией, частицам с меньшей энергией.
В нашем курсе будет рассматриваться передача теплоты путем теплопроводности.
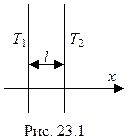Рассмотрим сначала одномерный случай, когда температура зависит только от одной координаты х. Пусть две среды разделены плоской перегородкой толщины l (рис. 23.1). Температуры сред Т 1 и Т 2 поддерживаются постоянными. Опытным путем можно установить, что количество тепла Q, переданное через участок перегородки площадью S за время t равно
, (23.1)
где коэффициент пропорциональности k зависит от материала стенки.
При Т 1 > Т 2 тепло переносится в положительном направлении оси х, при Т 1 < Т 2 – в отрицательном. Направление распространения тепла можно учесть, если в уравнении (23.1) заменить (Т 1 - Т 2)/ l на (- dT / dx). В одномерном случае производная dT / dx представляет собой градиент температуры. Напомним, что градиент – это вектор, направление которого совпадает с направлением наиболее быстрого возрастания скалярной функции координат (в нашем случае Т), а модуль равен отношению приращения функции при малом смещении в этом направлении к расстоянию, на котором это приращение произошло.
|
|
|
Чтобы придать уравнениям, описывающим перенос тепла, более общий и универсальный вид, ведем в рассмотрение плотность потока тепла j - количество тепла, переносимое через единицу площади в единицу времени
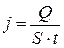. (23.2)
Тогда соотношение (23.1) можно записать в виде
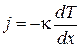. (23.3)
Здесь знак «минус» отражает тот факт, что направление теплового потока противоположно направлению градиента температуры (направлению ее возрастания). Таким образом, плотность потока тепла является векторной величиной. Вектор плотности потока тепла направлен в сторону уменьшения температуры.
Если температура среды зависит от всех трех координат, то соотношение (23.3) принимает вид
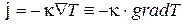, (23.4)
где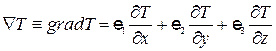 
, - градиент температуры (е 1, е 2, е 3 - орты осей координат).
Соотношения (23.3) и (23.4) представляют основной закон теплопроводности (закон Фурье): плотность потока тепла пропорциональна градиенту температуры. Коэффициент пропорциональности k называется коэффициентом теплопроводности (или просто теплопроводностью). Т.к. размерность плотности потока тепла [ j ] = Дж/(м2с), а градиента температуры [ dT/dx ] = К/м, то размерность коэффициента теплопроводности [k] = Дж/(м×с×К).
В общем случае температура в различных точках неравномерно нагретого вещества меняется с течением времени. Рассмотрим одномерный случай, когда температура зависит только от одной пространственной координаты х и времени t,и получим уравнение теплопроводности - дифференциальное уравнение, которому удовлетворяет функция T = T (x, t).
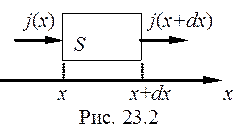Выделим мысленно в среде малый элемент объема в виде цилиндра или призмы, образующие которого параллельны оси х, а основания перпендикулярны (рис 23.2). Площадь основания S, а высота dx. Масса этого объема dm = r Sdx, а его теплоемкость c×dm где r - плотность вещества, с - удельная теплоемкость. Пусть за малый промежуток времени dt температура в этом объеме изменилась на dT. Для этого вещество в объеме должно получить количество тепла, равное произведению его теплоемкости на изменение температуры: 
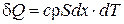. С другой стороны, d Q можно может поступить в объем только через основания цилиндра: 
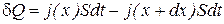(плотности потоков тепла j могут быть как положительными, так и отрицательными). Приравнивая выражения для d Q, получим
|
|
|
.
Заменяя отношения малых приращений соответствующими производными, придем к соотношению
. (23.5)
Подставим в формулу (23.5) выражение (23.3) для плотности потока тепла
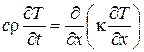. (23.6)
Полученное уравнение называется уравнением теплопроводности. Если среда однородна, и теплопроводность k не зависит от температуры, уравнение принимает вид
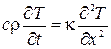, (23.7)
или
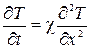, (23.8)
где постоянная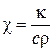 
называется коэффициентом температуропроводности среды.
Уравнениям (23.6) – (23.8) удовлетворяет бесчисленное множество функций T = T (x, t).
Для выделения единственного решения уравнения теплопроводности необходимо к уравнению присоединить начальные и граничные условия.
Начальное условие состоит в задании распределения температуры в среде Т (х,0) в начальный момент времени t = 0.
Граничные условия могут быть различными в зависимости от температурного режима на границах. Чаще всего встречаются ситуации, когда на границах заданы температура или плотность потока тепла как функции времени.
В ряде случаев в среде могут оказаться источники тепла. Теплота может выделяться в результате прохождения электрического тока, химических или ядерных реакций. Наличие источников тепла можно учесть введением объемной плотности энерговыделения q (x, y, z), равной количеству теплоты, выделяемому источниками в единице объема среды за единицу времени. В этом случае в правой части уравнения (23.5) появится слагаемое q:
.
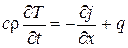В соответствии с этим изменятся и остальные уравнения.
|
|
|
