 |
Простейшие стационарные задачи теории теплопроводности
|
|
|
|
В стационарных задачах теории теплопроводности рассматриваются ситуации, когда распределение температуры в системе не меняется с течением времени.
1. Найдем распределение температуры в протяженной плоской пластине толщины l вдали от ее краев. Поверхности пластины поддерживаются при постоянных температурах Т 1 и Т 2 (рис. 24.1). Начало координат поместим на плоскости, ограничивающей пластинку слева. Ось х перпендикулярна пластине.
В стационарном случае температура в точках пластинки зависит только от координаты х и не зависит от времени. Тогда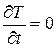 
, и из уравнения (23.5) следует 
, т.е. плотность потока тепла постоянна. Вывод о постоянстве плотности потока тепла можно сделать и без ссылки на уравнение теплопроводности (23.5). Выделим мысленно внутри пластинки элемент объема в виде цилиндра или призмы, образующие которого параллельны оси х, а основания перпендикулярны. Так как температура внутри пластинки не меняется со временем, количество тепла, поступившего в этот объем в единицу времени, должно быть равно вышедшему количеству тепла. Значит, плотности потока тепла на основаниях выбранного объема должны быть одинаковы. Поэтому
.
Если пластинка однородна и k не зависит от температуры 
. Обозначая константу буквой А и интегрируя, получим
,
где В – еще одна постоянная интегрирования. Постоянные А и В можно найти из граничных условий. При х = 0 температура Т (0) = Т 1, а при х = l T (l) = T 2. Эти условия приводят к системе уравнений
T 1 = B,
T 2 = Al + B.
Определив из нее постоянные А и В, найдем распределение температуры:
.
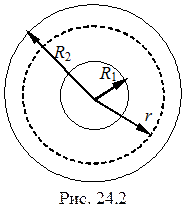2. Найдем стационарное распределение температуры T (r) между двумя коаксиальными (имеющими общую ось) бесконечно длинными цилиндрами (рис. 24.2). Радиус внутреннего цилиндра обозначим R 1, внешнего – R 2. Пространство между цилиндрами заполнено однородным веществом. Температуры цилиндров поддерживаются постоянными и равными соответственно Т 1 и Т 2. Для определенности будем считать, что Т 1 > Т 2. Из симметрии рассматриваемой задачи следует, что во всех точках цилиндрической поверхности радиуса r (R 1 < r < R 2) температура одинакова. Градиент температуры dT / dr, а значит и вектор плотности потока тепла j направлены вдоль радиуса.
|
|
|
В установившемся режиме температура вещества в пространстве между цилиндрами не меняется со временем. Поэтому количества теплоты, проходящие в единицу времени через поверхности внутреннего и внешнего цилиндров, а также и через любую цилиндрическую поверхность между ними, должны быть одинаковы.
Учитывая, что площадь боковой поверхности цилиндра пропорциональна его радиусу r, последнее условие можно записать в виде:
.
Если можно пренебречь зависимостью коэффициента теплопроводности k от температуры, его можно внести в константу. Обозначая постоянную буквой А, получим
или 
.
После интегрирования имеем
, (24.1)
где В - константа интегрирования.
Как и в предыдущем случае, константы А и В определяем из граничных условий.
Решая эту систему, получим 
После подстановки в (24.1) найдем распределение температуры T (r) в пространстве между цилиндрами
3. Рассмотрим задачу, в которой присутствуют источники тепла.
Найдем распределение температуры T (r) внутри шара радиуса R, в котором в результате какого-либо процесса (например, радиоактивного распада) происходит выделение тепла (рис.24.3). Количество тепла, выделяющееся в единицу времени в единице объема обозначим q. Будем считать, что q одинаково по всему объему и не меняется со временем. Теплопроводность вещества шара k. Температура Т 0 на поверхности шара поддерживается постоянной.
|
|
|
В установившемся режиме температура внутри шара перестанет зависеть от времени. Тогда количество тепла, которое выделяется в единицу времени внутри сферической поверхности радиуса r должно быть равно количеству тепла, проходящему в единицу времени через эту поверхность
Проведя сокращения и разделив переменные, придем к уравнению
Интегрируя, получим
,
где В – постоянная интегрирования. Ее определим из граничного условия T (R) = T 0.
Окончательно получим
Температура в центре шара
|
|
|
